In diesem Beitrag werde ich einige Themen aus der Schule fortsetzen, die vielleicht nicht genug betont wurden, aber dein Leben im Studium sehr erleichtern werden.
Das ist bereits Teil 5 – wenn du gerade erst hier reingesprungen bist, kannst du dir die vorherigen 4 Beiträge ansehen 🙂
Hier werde ich mich mit dem beidseitigen Multiplizieren und Teilen von Ungleichungen beschäftigen.
Ungleichungen teilen? Ich glaube, ich weiß, worum es geht…
Ja. Wir alle wissen (obwohl wir es manchmal vergessen) über die Änderung des Ungleichheitszeichens beim Multiplizieren/Teilen durch eine negative Zahl.
Zum Beispiel:
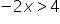/:(-2)
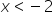(das Ungleichheitszeichen hat sich geändert, weil ich beide Seiten durch eine negative Zahl geteilt habe)
oder:
/
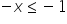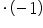
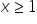(das Ungleichheitszeichen hat sich nach dem Multiplizieren beider Seiten mit einer negativen Zahl geändert)
Aber was ist mit dem Multiplizieren und Teilen nicht durch eine ZAHL, sondern durch eine VARIABLE, zum Beispiel:
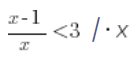
Können wir diese Multiplikation durchführen und mit:
…?
Die richtige Antwort ist: NEIN, KÖNNEN WIR NICHT.
Wir erinnern uns an die Regel: „Wenn wir mit einer positiven Zahl multiplizieren, ändern wir das Zeichen nicht, wenn wir mit einer negativen Zahl multiplizieren, ändern wir es“. Beim Multiplizieren mit einer Variablen 
WISSEN WIR NICHT, ob wir mit einer positiven oder negativen Zahl multiplizieren. Die Variable könnte gleich -100 sein oder auch gleich 15. Dass kein Minuszeichen davor steht, ändert nichts (sie könnte trotzdem negativ sein).
Wenn wir das nicht wissen, können wir nicht zu…
…übergehen, denn wir könnten diese Ungleichung nur erhalten, wenn wir mit einer positiven Zahl multiplizieren (ohne das Zeichen zu ändern), und das WISSEN WIR NICHT.
Die gleiche Regel gilt für die Division, daher können wir so etwas nicht tun:
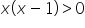/:x
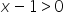
…denn, noch einmal wiederholt: wir wissen nicht, ob x eine positive oder negative Zahl ist.
Zusammenfassend also
Wir teilen nicht beidseitig Ungleichungen mit Variablen.
Und noch….
Interessante Tatsache
Wenn wir – auf irgendeine Weise – wissen, dass die Variable (oder der gesamte Ausdruck), durch die wir beidseitig multiplizieren/teilen wollen, immer positiv (oder negativ) ist, können wir bedenkenlos multiplizieren/teilen.
Zum Beispiel, wenn die Definitionsmenge (es wird später noch einen Wiederholungspost zur Definitionsmenge geben) die Menge der Zahlen 
ist, dann wissen wir, dass definitiv positiv ist.
Dann KÖNNEN wir…
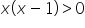/:x
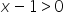
…machen, müssen aber daran denken, die Definitionsmenge in der Lösung zu berücksichtigen (nur 
.
