Einige Dinge, die du in der Mittelschule gut hättest lernen sollen, aber niemand hat es dir gesagt – Teil 2: Quantoren

---

Quantoren – aber die gab es eigentlich gar nicht…

Na gut, ich bin mir nicht zu 100% sicher, ob Quantoren nach den regelmäßigen jährlichen Stoffkürzungen überhaupt noch in der Oberstufe vorhanden sind. Ich habe auch keine Lust, das nachzuprüfen, denn warum sich aufregen.

Sie sollten immer noch im erweiterten Profil sein. Wirklich sollten sie.

Na gut, aber wer braucht das?

In den meisten mathematischen Definitionen und Theoremen werden Begriffe wie: “jeder” und “es gibt” verwendet.

Meistens in etwas komplexeren Sequenzen, zum Beispiel: “zwischen jeder zwei Zahlen gibt es unendlich viele Zahlen” (das ist etwas halbformal und ungenau), oder: “für jede nicht-negative reelle Zahl existiert genau eine Wurzel”, oder: “es gibt irgendetwas, dass für jedes andere irgendetwas gibt es noch ein anderes irgendetwas” (das ist die mathematische Definition eines anderen irgendetwas).

Im Studium erhältst du eine ganze Menge von solchen Definitionen und Theoremen, die schnell und nacheinander in der Vorlesung diktiert werden oder – schlimmer noch – direkt in Form von:

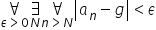
So wäre es gut (anstatt die Hand zu heben und den Professor zu fragen, ob man es “neu zeichnen” soll), dass du schon von Anfang an gelernt hast, solche Formeln richtig zu lesen. Du könntest dann sofort zu den Phasen des “Einarbeitens” in die Definition, einigen Beobachtungen “wie es funktioniert” an konkreten Beispielen usw. übergehen.

Allgemeiner und spezieller Quantor – Lernen wir sie besser kennen

“jeder”, “für jeden” – das ist ein allgemeiner Quantor, bezeichnet als: .

“existiert”, “es gibt” – das ist ein spezieller Quantor, bezeichnet als: .

Ich verwende und empfehle diese speziellen Quantor-Symbole, weil sie definitiv nicht verwechselt werden.

– ist ein umgedrehtes großes A (vom englischen “all” – jeder).

– ist ein umgedrehtes großes E (vom englischen “exists” – existiert).

Es gibt auch andere Symbole für Quantoren: Λ (“für jeden”) und V (“existiert”) – aber mit denen werde ich mich nicht beschäftigen, weil sie jeder verwechselt.

Mathematische Formeln, die mit Quantoren geschrieben sind

Die einfachsten Formeln haben die Form:

– wir lesen: “für jedes x” (kann auch geschrieben werden als: , aber es wird wieder verwirrt, also mache ich es nicht)

– wir lesen: “es gibt x”

Jedoch sind Formeln im Allgemeinen komplizierter, zum Beispiel:

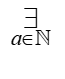– wir lesen: “es gibt ein a, das eine natürliche Zahl ist”, oder: “es gibt ein a, das zu den natürlichen Zahlen gehört”, oder irgendein anderer Ausdruck im Deutschen, der den Kern der Sache widerspiegelt, nämlich dass:

1. Es gibt ein a

2. a ist eine natürliche Zahl

Es gibt hier keine “starren” Sprachregeln darüber, was jedes Wort sein muss und ob es “es gibt ein a” oder “es gibt so ein a” sein muss.

Formeln können und müssen in der Regel miteinander kombiniert werden, zum Beispiel:

\underset{x>4}{\mathop{\forall }}\,\underset{n\in\mathbb{N}}{\mathop{\exists }}\,

bedeutet:

“für jedes x>4 gibt es ein n, das zu den natürlichen Zahlen gehört”

Wir verstehen darunter, dass für jedes x>4 ein n gefunden wird, das zu den natürlichen Zahlen gehört, so dass für jedes solche x das entsprechende n ausgewählt wird. Quantoren stehen in einem logischen Zusammenhang miteinander, es sind keine zwei unabhängigen Formeln, die nebeneinander geschrieben sind.

Mehr noch…

Die Reihenfolge spielt eine Rolle

Die gleiche Formel wie die letzte, aber mit vertauschter Reihenfolge der Quantoren:

\underset{n\in \mathbb{N} }{\mathop{\exists }}\,\underset{x>4}{\mathop{\forall }}\,

…lesen wir anders:

“es gibt ein a, das eine natürliche Zahl ist, so dass für jedes x größer als 4…”

Wir verstehen, dass wir zuerst ein n haben (von dem wir wissen, dass es existiert) und nur für dieses bestimmte n passiert etwas für alle x>4.

Beispiel – Exkurs

Ein klassisches Beispiel ist hier die Definition der gleichmäßigen und punktweisen Konvergenz einer Funktionfolge, die sich nur durch… die Reihenfolge der Quantoren unterscheidet (ich habe diese Definitionen etwas vereinfacht):

Punktweise Konvergenz:

Gleichmäßige Konvergenz:

In der Definition der gleichmäßigen Konvergenz landet der Quantor, der am Anfang der punktweisen Konvergenz stand, am Ende. Ohne ins Detail zu gehen, ändert dies die Bedeutung der gesamten Formel.

Bei der punktweisen Konvergenz nahmen wir ZUERST (wir lesen von links) ein beliebiges x, dann lasen wir die Formel und kamen zu dem Schluss, dass für dieses am Anfang festgelegte x die Abstände zwischen den Werten der Funktionen in der Folge und der “Grenzfunktion” ins Unendliche abnehmen.

Bei der gleichmäßigen Konvergenz stellten wir ZUERST fest, dass der Abstand zwischen den Werten der entsprechenden Funktionen ins Unendliche abnimmt, und dann kamen wir zu dem Schluss, dass dies für jedes x geschieht.

Definitionen und Theoreme schreiben

Wenn man weiß, wie man Quantoren liest, ist das Schreiben mathematischer Definitionen und Theoreme für uns bereits geöffnet. Zum Beispiel:

\underset{x\in\mathbb{R}}{\mathop{\forall }}\,{{x}^{2}}\ge 0

Wir lesen es als: “Für jede reelle Zahl x ist x zum Quadrat größer oder gleich null”, oder schöner: “Jede Zahl x zum Quadrat ist nicht negativ” – Ich bin definitiv dafür, Definitionen und Theoreme in einer bunteren Sprache zu lesen.

Der obige Satz ist WAHR. Wir haben kein Problem damit, auch FALSCHE Sätze zu schreiben:

\underset{a>0}{\mathop{\exists }}\,\underset{x>a}{\mathop{\forall }}\,\frac{a}{x}>1

Das würden wir lesen: “Es gibt eine positive Zahl a, so dass für jede Zahl x größer als dieses a, a geteilt durch x größer als 1 ist”, was natürlich FALSCH ist (weil eine positive Zahl, die durch eine größere Zahl geteilt wird, niemals größer als 1 sein wird und es keine solche Zahl gibt).

Und jetzt nehmen wir die Definition der Grenze einer Folge aus dem vorherigen Post:

Wir lesen es so (mit einigen Erklärungen):

“Für jedes größer als null finden wir eine Folgengliednummer , so dass für jedes Folgenglied mit einer Nummer größer als der Abstand (der Betrag ist der Abstand) zwischen diesem Folgenglied und dem Grenzwert kleiner als ist”

Wir können auch eine menschlichere Sprache verwenden:

“Egal wie klein der Anfangsabstand ist, wir finden eine Folgengliednummer, so dass alle nachfolgenden Glieder dieser Folge näher an der Grenze liegen als der am Anfang festgelegte Abstand “