Ein paar Dinge, die du in der Oberstufe gut lernen solltest, aber dir niemand gesagt hat – Teil 3: Quadratische Funktion

---

Dieser Beitrag ist bereits der dritte in Folge, in dem ich auf Dinge aufmerksam machen möchte, die es sich lohnt, am Anfang des Mathematikstudiums an der Universität zu wiederholen. Ein schneller Überblick über diese Themen wird dein Leben an der Universität erheblich erleichtern. In den vorherigen Beiträgen habe ich folgende Themen behandelt:

Geometrische Interpretation des Absolutwerts

Quantoren

Heute ist die quadratische Funktion an der Reihe.

Quadratische Funktion? Aber das haben wir doch zwei Monate lang gemacht…

Das Thema der quadratischen Funktion ist natürlich sehr breit gefächert, und ich meine keinesfalls, dass du ein Lehrbuch aus der Oberstufe nehmen und das gesamte Kapitel von Anfang bis Ende durcharbeiten sollst.

Konzentrieren wir uns nur auf einige wichtige Details, Nuancen und Fallen.

Quadratische Funktion vs. quadratische Gleichung

Quadratische Funktion ist natürlich etwas wie das:

oder: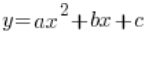

Wo beliebige Zahlen sind. Beispiele für quadratische Funktionen sind:

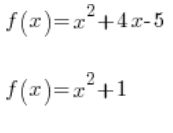
usw…

Das Konzept der quadratischen Funktion sollte vom Konzept der quadratischen Gleichung unterschieden werden, zum Beispiel:

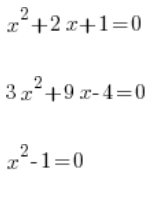
usw…

Das ist nicht dasselbe!!!!

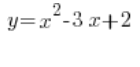ist eine quadratische Funktion, während 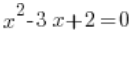eine quadratische Gleichung ist.

Das Nichtunterscheiden zwischen Funktion und Gleichung führt oft zu…

Grausamer Fehler Nummer 1

Zum Beispiel beim Berechnen von Ableitungen und gegeben einer Funktion:

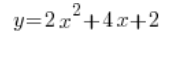
Machen Leute oft so etwas:

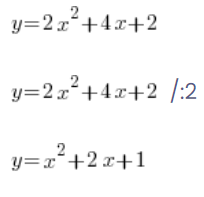
…und rechnen weiter, was nötig ist.

Sie machen diesen Fehler, weil sie sich erinnern, dass man so etwas bei Gleichungen machen konnte:

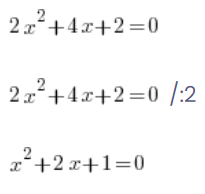
…und bei Gleichungen ist alles in Ordnung, man kann beide Seiten teilen, 0 auf der rechten Seite durch 2 geteilt gibt tatsächlich 0 und die Gleichungen sind äquivalent (haben dieselben Lösungen).

Aber das kann man bei Funktionen nicht machen – man müsste doch irgendwie auch das y auf der linken Seite teilen usw. Durch einfaches Teilen des Funktionswerts durch 2 erhält man eine andere Funktion!

Was solltest du von Funktionen wiederholen?

Nicht viel. Eigentlich nur zwei Formen der Funktion: kanonisch und faktorisierte.

Die kanonische Form der quadratischen Funktion

Ich gehe davon aus, dass wir bereits die allgemeine Form der quadratischen Funktion haben:

Ihre kanonische Form ist:

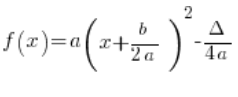
Das heißt:

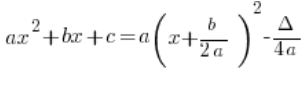
Was a, b und sind, ist bekannt, kaum jemand hat ein Problem damit, .

Man kann sogar bemerken, dass, wenn wir in der kanonischen Form vor die Klammer ziehen, wir erhalten:

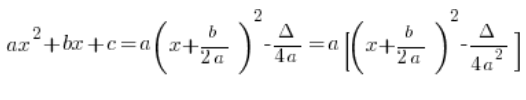
…was manchmal nützlich sein kann und manchmal nicht unbedingt.

Wenn du das gelernt hast, indem du die Koordinaten des Scheitelpunkts berechnet hast (normalerweise als und ) und in die Formel eingetragen hast:

dann ist es natürlich etwas umständlich, aber auch gut.

Denke an am Anfang der kanonischen Form!

Die faktorisierte Form der quadratischen Funktion (ihre Zerlegung in Faktoren):

Kehren wir nun zu unserer allgemeinen quadratischen Funktion zurück:

Sehr oft wird man sie “in Faktoren zerlegen” müssen, wobei man die faktorisierte Form der quadratischen Funktion verwendet:

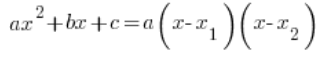
Wo und berechnet werden aus den bekannten und beliebten Formeln:

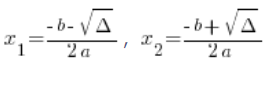
Auch hier musst du an am Anfang der Formel denken!!!

Beachte auch, dass diese und nicht immer existieren (wenn Δ negativ ist, existieren sie nicht), was bedeutet, dass die Funktion nicht immer in faktorisierter Form geschrieben werden kann, d. h. eine quadratische Funktion kann nicht immer in Faktoren zerlegt werden.

Was solltest du von quadratischen Gleichungen wiederholen?

Bei quadratischen Gleichungen vermute ich, dass die Dinge nicht allzu schlecht stehen. Wir schaffen es in der Regel, die allgemeine Gleichung zu lösen:

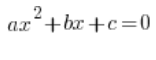
Zum Beispiel:

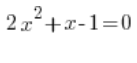
Wir rechnen einfach:

Dann, wenn Δ nicht negativ ist, Lösungen der Gleichung:

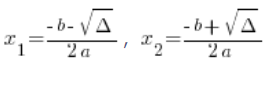
Denke daran, dass dort im Nenner steht und nicht einfach nur 2!

Ich möchte jedoch bei einem speziellen Fall der Gleichung innehalten:

Hier passieren viele Fehler. Zum Beispiel:

Grausamer Fehler Nummer 2

Worin besteht der Fehler genau? Die Zahl 2 ist tatsächlich eine Lösung der Gleichung , aber die zweite Lösung dieser Gleichung, nämlich die Zahl -2, wurde völlig ignoriert. Es sollte sein:

Negative Lösungen können nur in der Geometrie ignoriert werden (weil der Abstand nicht negativ sein kann).

Ein weiteres Problem mit der Gleichung in der Form: ist:

Grausamer Fehler Nummer 3

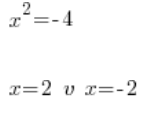
Was natürlich Unsinn ist, weil 2 zum Quadrat nicht -4 ergibt. Tatsächlich ergibt nichts zum Quadrat -4 (diejenigen, die bereits komplexe Zahlen studiert haben, schweigen still). Die Gleichung:

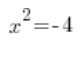
…hat überhaupt keine Lösungen.

Also sei wachsam. Die Gleichung hat zwei Lösungen und die Gleichung hat überhaupt keine Lösungen.

Ich lade dich ein, ruhig alles, was bisher gesagt wurde, noch einmal zu wiederholen und natürlich Fragen in den Kommentaren zu stellen.