Beim Lösen von Aufgaben mit komplexen Zahlen muss man beachten, dass eine komplexe Zahl in trigonometrischer Form so aussieht:
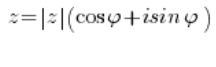
Und nur so. Nicht mehr, nicht weniger.
Man sollte also darauf achten:
Wann ist eine komplexe Zahl in trigonometrischer Form und wann nicht?
- Die Zahl:
IST in trigonometrischer Form, wobei der Betrag der Zahl gleich 1 ist (), weil natürlich:
- Die Zahl: ist NICHT in trigonometrischer Form, weil vor der imaginären Einheit ‚i‘ multipliziert mit Sinus ein Minus steht, es sollte aber ein Plus sein.
Um diese Zahl in die trigonometrische Form zu überführen, müssen wir trigonometrische Formeln verwenden:
Mit diesen Formeln können wir umformen:
Sinus- und Kosinusfunktionen sind-periodisch, daher ist ihr Wert derselbe wie . Mehr dazu habe ich in: diesem Beitrag geschrieben.
Also haben wir am Ende:
…und das ist eine Zahl in trigonometrischer Form. - Die Zahl: ist NICHT in trigonometrischer Form, weil vor der imaginären Einheit ‚i‘ multipliziert mit Sinus ein Minus steht, es sollte aber ein Plus sein, und vor dem Kosinus ein Minus steht, es sollte aber ein Plus sein.
Um diese komplexe Zahl in die trigonometrische Form zu überführen, müssen wir das Minus vor der Klammer herausziehen:
Die Zahl in die trigonometrische Form umwandeln (das können wir schon…):
Also haben wir die Multiplikation von zwei Zahlen in trigonometrischer Form:
Um Zahlen in trigonometrischer Form zu multiplizieren, multiplizieren wir ihre Beträge und addieren ihre Argumente (es gibt eine Formel dafür), also haben wir:
Und das ist eine Zahl in trigonometrischer Form. - Die Zahl: ist KEINE komplexe Zahl in trigonometrischer Form, weil vor dem Kosinus ein Minus steht, es sollte aber ein Plus sein.
Um diese komplexe Zahl in trigonometrische Form zu bringen, muss das Minuszeichen vor der Klammer herausgezogen werden:
Die Zahl -1 muss in trigonometrische Form umgewandelt werden (das haben wir in Punkt 3 gemacht), ebenso muss die Zahl in trigonometrische Form umgewandelt werden (das haben wir in Punkt 2 gemacht).
Wir erhalten:
Unter Verwendung der Formel für die Multiplikation von trigonometrischen Funktionen:
Und unter Verwendung der Periodizität der Sinus- und Kosinusfunktionen:
- Die Zahl: ist KEINE komplexe Zahl in trigonometrischer Form, weil vor dem Kosinus eine imaginäre Einheit ‚i‘ steht (und das sollte nicht dort sein), und vor dem Sinus keine imaginäre Einheit ‚i‘ steht.
Man muss die aus der Schule bekannten trigonometrischen Formeln verwenden:
Also haben wir:
Und das ist eine komplexe Zahl in trigonometrischer Form. - Die Zahl: ist KEINE komplexe Zahl in trigonometrischer Form.
Man muss den Sinus und Kosinus tauschen, genau wie wir es in Punkt 5 gemacht haben, und dann lösen, wie wir es in Punkt 4 gemacht haben. - Die Zahl: ist KEINE komplexe Zahl in trigonometrischer Form.
Man muss den Sinus und Kosinus tauschen, genau wie wir es in Punkt 5 gemacht haben, und dann lösen, wie wir es in Punkt 2 gemacht haben. - Die Zahl: ist KEINE komplexe Zahl in trigonometrischer Form.
Man muss den Sinus und Kosinus tauschen, genau wie wir es in Punkt 5 gemacht haben, und dann lösen, wie wir es in Punkt 3 gemacht haben.
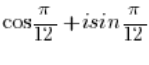IST in trigonometrischer Form, wobei der Betrag der Zahl gleich 1 ist (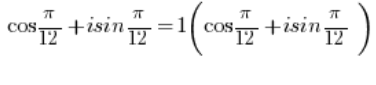
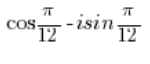), weil natürlich:
ist NICHT in trigonometrischer Form, weil vor der imaginären Einheit ‚i‘ multipliziert mit Sinus ein Minus steht, es sollte aber ein Plus sein.
-periodisch, daher ist ihr Wert derselbe wie 
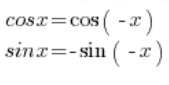
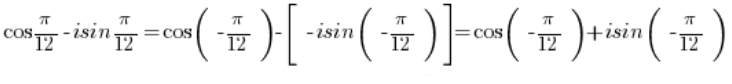
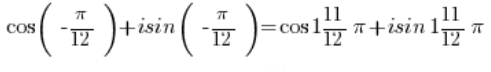
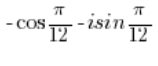ist NICHT in trigonometrischer Form, weil vor der imaginären Einheit ‚i‘ multipliziert mit Sinus ein Minus steht, es sollte aber ein Plus sein, und vor dem Kosinus ein Minus steht, es sollte aber ein Plus sein.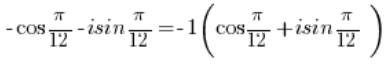
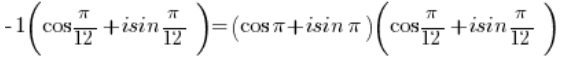
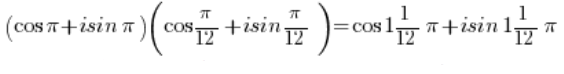
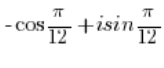in die trigonometrische Form umwandeln (das können wir schon…):
ist KEINE komplexe Zahl in trigonometrischer Form, weil vor dem Kosinus ein Minus steht, es sollte aber ein Plus sein.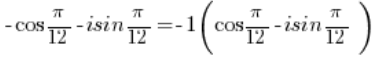
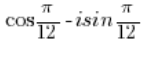in trigonometrische Form umgewandelt werden (das haben wir in Punkt 2 gemacht).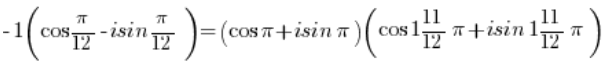
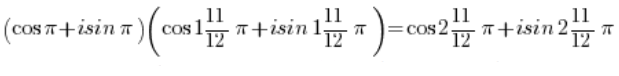
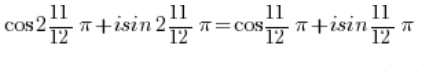
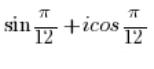ist KEINE komplexe Zahl in trigonometrischer Form, weil vor dem Kosinus eine imaginäre Einheit ‚i‘ steht (und das sollte nicht dort sein), und vor dem Sinus keine imaginäre Einheit ‚i‘ steht.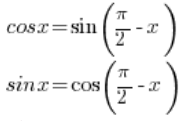
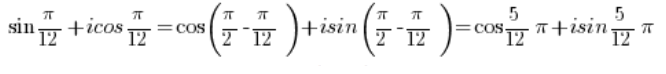
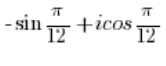ist KEINE komplexe Zahl in trigonometrischer Form.
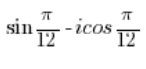ist KEINE komplexe Zahl in trigonometrischer Form.
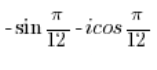ist KEINE komplexe Zahl in trigonometrischer Form.Viel Glück! 🙂
