Es befinden sich momentan keine Produkte im Warenkorb.
Krystian Karczyński- 22 April 2024
- Komentarz 0
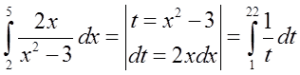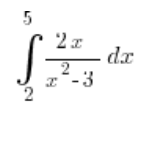
Um das obige Problem bezüglich des bestimmten Integrals zu lösen, müssen wir die Substitution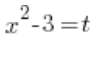 
anwenden, da sind wir uns einig. Aber was ist mit den Integrationsgrenzen?
Integrationsgrenzen bei Substitutionsaufgaben für bestimmte Integrale
Können wir schreiben:
?
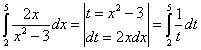Natürlich nicht. Das Problem mit den Integrationsgrenzen. Im bestimmten Integral links beziehen sich diese auf die Variable 
, und rechts auf die Variable 
, daher müssen sie auch mit der Variablen geändert werden.
Ein Ansatz (den ich in meinem Kurs empfehle) ist, das Problem komplett zu umgehen, indem man das unbestimmte Integral (ohne Integrationsgrenzen) nebenbei löst und dann die Integrationsgrenzen 5 und 2 in das Ergebnis (mit Variable x) einsetzt.
Der andere Ansatz ist, das Problem direkt anzugehen und die Integrationsgrenzen entsprechend der Substitution zu ändern. Da die Grenzen in der Variablen x 2 und 5 sind, nach der Substitution: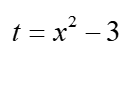 
werden sie in der Variablen t entsprechend 1 und 22 sein, und diese Ergebnisse erhielt ich, indem ich 2 und 5 für x in die Substitution 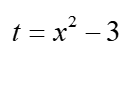einsetzte. Der richtige Übergang wäre also:
