Richtungsableitungen – schon wieder etwas Neues?

---

Ort und Zeit der Handlung

Die Berechnung von Richtungsableitungen als Thema zum Lernen (also zum Bestehen) folgt eigentlich direkt nach den partiellen Ableitungen von Funktionen mehrerer Variablen, die die meisten Studierenden im zweiten Semester durchnehmen.

Es ist ein Thema, das so selten behandelt wird, dass ich es nicht in meinen Kurs zu partiellen Ableitungen aufgenommen habe, aber oft genug, dass ich es auf den Blog stelle – zum Nutzen derjenigen, die Richtungsableitungen lernen müssen, und derjenigen, die einfach neugierig sind, worum es geht. Ich möchte jedoch betonen, dass ich mich wie in den Kursen heute fast ausschließlich auf die Praxis konzentrieren werde (“wie mache ich das?”), und nicht auf die Theorie (“was mache ich eigentlich?”).

Richtungsableitungen – wie mache ich das?

Im Falle der Richtungsableitung haben wir es mit der gleichzeitigen Zunahme der Argumente x und y zu tun, was natürlich einer bestimmten Zunahme des Funktionswertes entspricht.

Für die Aufgabe benötigen wir drei Dinge:

1. Eine Funktion, von der wir die Richtungsableitung berechnen.
2. Einen Punkt, an dem wir die Richtungsableitung berechnen.
3. Eine Richtung, die in Form eines Vektors angegeben ist.

Mit dem oben genannten wird die Aufgabe darauf reduziert, den Vektor in einen Richtungsvektor umzuwandeln (etwas aus der analytischen Geometrie, ich werde gleich zeigen, wie das geht), und ihn dann in die Formel einzusetzen:

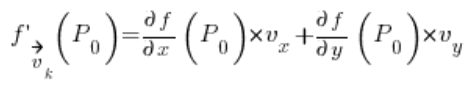
In dem:

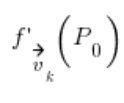ist die Richtungsableitung an dem Punkt in Richtung des Vektors

ist der Punkt, an dem wir die Richtungsableitung berechnen

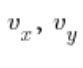sind die Koordinaten des Richtungsvektors

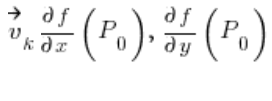sind die partiellen Ableitungen der Funktion an dem Punkt .

Berechne die Richtungsableitung der Funktion 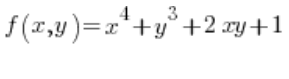an dem Punkt P(1,2) in Richtung .

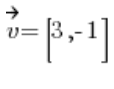Lösung:

Alles ist bereit, wir müssen nur den Vektor 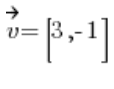in einen Richtungsvektor umwandeln.

Ein Richtungsvektor ist ein Vektor mit derselben Richtung (wer hätte das gedacht), derselben Ausrichtung, aber einer Länge von 1.

Er wird durch die Formel berechnet:

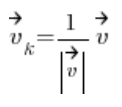
Einfach ausgedrückt, teilen wir seine Koordinaten durch seine Länge.

Also berechnen wir die Länge des Vektors :

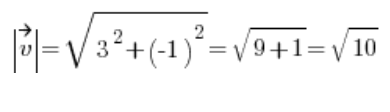
Dann erhalten wir den Richtungsvektor:

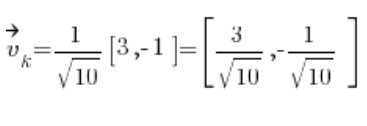
Für die Formel der Richtungsableitung benötigen wir noch die partiellen Ableitungen der Funktion 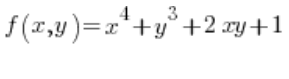an dem Punkt P(1,2):

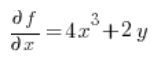
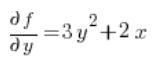
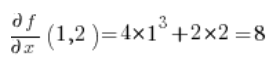
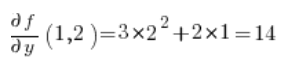
Und jetzt haben wir alles, was wir für die Formel brauchen:

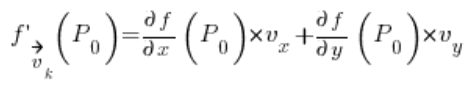
Einfach einsetzen, und wir haben das Ergebnis: .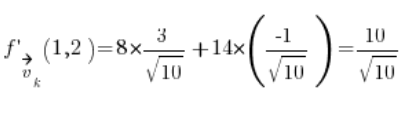

Fertig.

Beispiel 2

Finde die Richtungsableitung der Funktion: 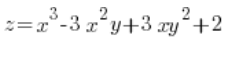an dem Punkt P(3,1) in der Richtung von diesem Punkt zu dem Punkt Q(6,5).

Lösung:

Die Aufgabe ist etwas schwieriger, weil der Richtungsvektor nicht direkt angegeben ist, aber das macht nichts.

Wir bewegen uns von Punkt P zu Punkt Q, also ist der Verschiebungsvektor [3,4].

Jetzt finden wir den Richtungsvektor, indem wir die Länge des Vektors [3,4] berechnen:

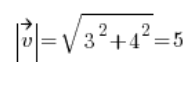
Und wir haben den Richtungsvektor:

Jetzt berechnen wir die partiellen Ableitungen an dem Punkt (3,1):

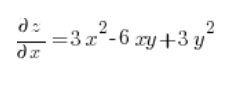
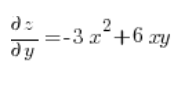
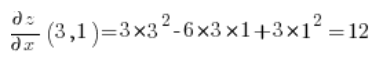
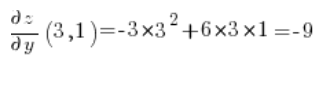
Dann setzen wir nur in die Formel der Richtungsableitung ein:

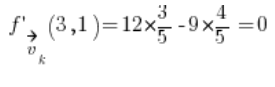
Beispiel 3

Finde die Richtungsableitung der Funktion 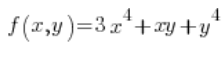an dem Punkt (1,2) in der Richtung, die einen Winkel von mit der positiven x-Achse bildet.

Lösung:

Die Aufgabe scheint schwieriger, da in den Daten kein Richtungsvektor vorhanden ist. Zeichnen wir jedoch die ganze Sache:

Es geht darum, die Koordinaten eines beliebigen Vektors in der angegebenen Richtung zu finden.

Wir verwenden die Tatsache, dass 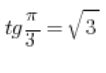und können annehmen, dass unser Vektor die Koordinaten 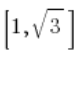hat, wie in der Zeichnung (es reichte, irgendeinen Vektor in Richtung der Linie zu wählen):

Und jetzt machen wir weiter wie gewohnt.

Wir berechnen den Richtungsvektor:

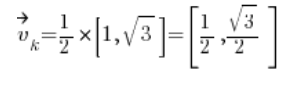
Dann die partiellen Ableitungen an dem Punkt (1,2):

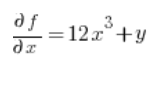
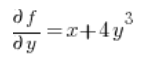
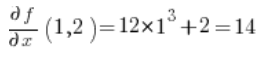
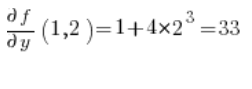
Wir setzen in die Formel ein, und wir haben das Ergebnis

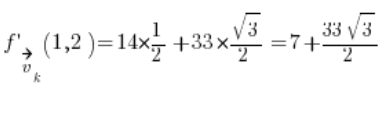
Ich freue mich wie immer über Fragen in den Kommentaren 🙂