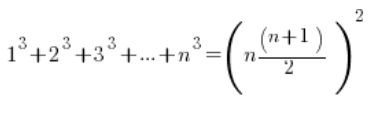Grenzwerte einer Folge mit der Summe der Quadrate oder der Summe der Kuben
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
In den Grenzen von Folgen sieht es manchmal so aus:
und manchmal sogar so:
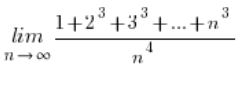
Was dann?
Die Antwort ist einfach:
Formeln für die Summe der Quadrate und die Summe der Kuben aufeinanderfolgender natürlicher Zahlen.
Sie gehen so:
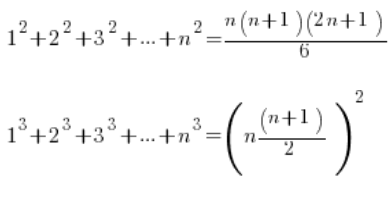
Formeln – wie alle Formeln – sind auswendig zu lernen. Wenn du ähnliche Beispiele hattest und sie wirklich brauchst.
Wenn man diese Formeln kennt, wird das Berechnen unserer Grenzen ganz einfach:
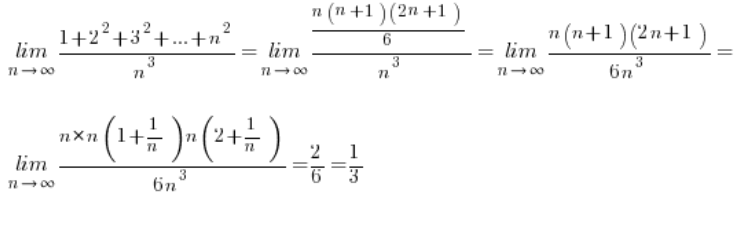
Nächste Grenze:
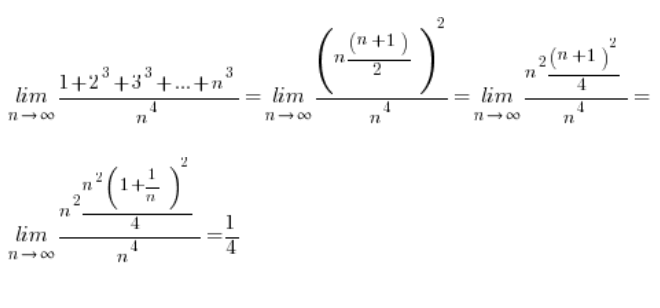
Induktive Beweise für Formeln
Die Gültigkeit der Formeln kann ziemlich leicht induktiv bewiesen werden (zumindest vor einigen Jahren war dies in der Schule Standard). Ich werde dies für die folgende Formel tun:
1. 
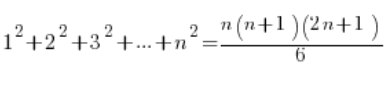
Induktionsschritt 1
Wir überprüfen die Gültigkeit der Formel für n=1:
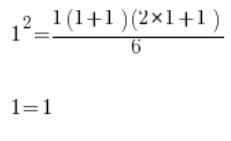
Stimmt
Induktionsschritt 2
Wir nehmen Annahme an, dass für eine natürliche Zahl n:
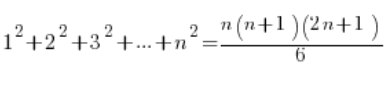
Induktionsschritt 3
Wir beweisen die These (unter Verwendung der angenommenen Annahme), dass die Formel auch für n+1 gilt, d.h.:
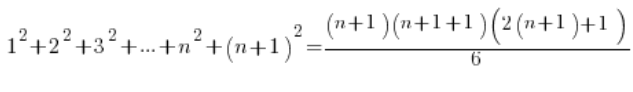
Auf der linken Seite setzen wir anstelle von 
die Formel aus der Annahme ein, auf der rechten Seite ordnen wir einfach:
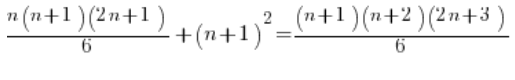
Und dann, anstatt es mit Gewalt zu erzwingen, arbeiten wir etwas subtiler:
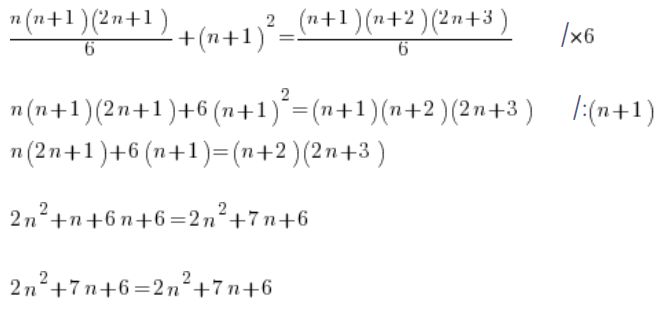
Also ist die These bewiesen. Die Formel ist induktiv bewiesen.
Ich lade euch ein, die zweite Formel induktiv zu beweisen, für die Summe der Kuben:
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
