Ich bekomme viele Fragen zu der von mir im Kurs über Unbestimmte Integrale eingeführten Formel für die kanonische Form einer quadratischen Funktion.
Die Formel:
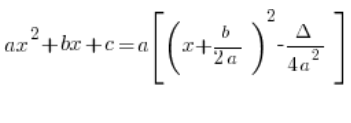
erscheint im Schema zur Lösung rationaler Integrale in Lektion 5 des Kurses:
Schema für rationale Integrale
Warum gibt es dort a^2?
Das Problem ist, dass es auf den ersten Blick anders aussieht als die kanonische Form, die aus der Schule bekannt ist:
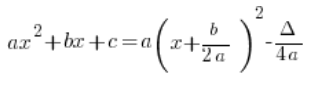
Die Standardfrage hier ist: „Warum ist bei Ihnen ![]() im Nenner?“
im Nenner?“
Transformation der Formel
Es reicht jedoch, zu bemerken, dass wenn wir in der Formel:
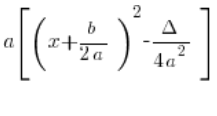
![]() mit der eckigen Klammer multiplizieren, wir genau die Formel erhalten:
mit der eckigen Klammer multiplizieren, wir genau die Formel erhalten:
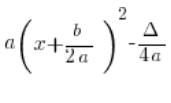
(nachdem ![]() mit dem Term
mit dem Term ![]() multipliziert wurde, kürzt es sich heraus und wir erhalten
multipliziert wurde, kürzt es sich heraus und wir erhalten ![]() )
)
Daher sind beide Formen äquivalent, was einfach bedeutet:
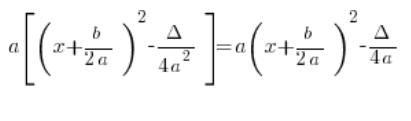
Warum also diese Formel mit der eckigen Klammer und a außerhalb der Klammer einführen? Weil es bei rationalen Integralen bequemer ist 🙂
In den späteren Schritten der Berechnung des Integrals müssen Sie ![]() trotzdem vor das Integrationszeichen bringen (und zuerst vor die Klammer im Nenner), warum also warten? 🙂
trotzdem vor das Integrationszeichen bringen (und zuerst vor die Klammer im Nenner), warum also warten? 🙂


