O co właściwie chodzi?
Ten wzorek wszyscy znamy:
\int{\frac{1}{x}dx}=\ln \left| x \right|+CTylko bardzo dociekliwi ludzie dumali by nad tym, skąd i po co komu ta wartość bezwzględna w argumencie logarytmu.
Chyba lepiej w ramach zdrowego nie dokładania sobie problemów po prostu zawsze ją przepisywać w odpowiedziach (wariant optymistyczny), albo po prostu pomijać i pisać sobie \int{\frac{1}{x}dx}=\ln \left( x \right)+C (wariant pesymistyczny).
Spójrzmy zresztą na Wolframa:
Tak, wygląda na to, że wszystko jest O.K. i można na przykład robić tak:
\int{\frac{1}{x-1}dx}=\left| \begin{matrix}t=x-1\\dt=dx\\\end{matrix} \right|=\int{\frac{1}{t}dt}=\ln t+C=\ln \left( x-1 \right)+CCzy rzeczywiście?
Pojawiają się problemy
Weź trochę trudniejszą całkę:
\int{\frac{1}{{{x}^{2}}-3x+2}dx}Licząc rozkładem na ułamki proste (jak to się dokładnie robi możesz sprawdzić w moim Kursie Video) masz:
\int{\frac{1}{{{x}^{2}}-3x+2}dx}=\int{\frac{1}{\left( x-1 \right)\left( x-2 \right)}dx}=\int{\frac{1}{x-2}dx}-\int{\frac{1}{x-1}dx}=\ln \left| x-2 \right|-\ln \left| x-1 \right|+CNo i w sumie pozamiatane, sprawdzasz tylko w Wolframie…
…?
I co my tu mamy?
Jakim cudem Twój wynik (prawidłowy): \ln \left| x-2 \right|-\ln \left| x-1 \right|+C ma się zgadzać w wynikiem Wolframa (prawidłowym): \ln \left( 2-x \right)-\ln \left( 1-x \right)+C?
Ano, zgadza się. Dla x-sów w określonej dziedzinie.
Skąd wartość bezwzględna we wzorze
Zacznę od podstaw, czyli skąd się wzięła ta wartość bezwzględna we wzorze:
\int{\frac{1}{x}dx}=\ln \left| x \right|+CJak pamiętasz, jakaś funkcja np. F(x) była „całką” innej funkcji np. f(x) wtedy, kiedy pochodna z niej dawała tą funkcję, tzn. wtedy, gdy: {F}'\left( x \right)=f\left( x \right).
Pochodna z funkcji lnx daje faktycznie funkcję \frac{1}{x}, czyli prawdą jest (jak twierdzi Wolfram), że \int{\frac{1}{x}dx}=\ln x+C – ale tylko dla x dodatnich ! Ten wzór obowiązuje tylko dla x należących do przedziału (0,\infty), bo tylko w tym przedziale możesz w ogóle policzyć pochodną z lnx (ze względu na to, że argumentem logarytmu nie może być liczba ujemna).
A co, jeśli x będą ujemne? Ile równa będzie całka \int{\frac{1}{x}dx}? Dla x-sów ujemnych oczywiście:
\int{\frac{1}{x}dx}=\ln \left( -x \right)+CJeżeli x-sy są ujemne, to -x jest dodatnie (czyli logarytm istnieje) i pochodna z niego:
{{\left( \ln \left( -x \right) \right)}^{\prime }}=\frac{1}{-x}\cdot {{\left( -x \right)}^{\prime }}=\frac{1}{-x}\cdot \left( -1 \right)=\frac{1}{x}Czyli faktycznie \int{\frac{1}{x}dx}=\ln \left( -x \right)+C – dla x ujemnych !
Masz więc:
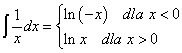
No a teraz korzystając z prostej definicji wartości bezwzględnej ![]() masz:
masz:
dla x-sów różnych od zera.
Podsumowanie
Jeśli w rozwiązywanej przez Ciebie całce wyjdzie Ci w wyniku na przykład \ln \left| x-2 \right|, a w odpowiedziach będzie \ln \left( 2-x \right), to znaczy, że masz dobrze, ponieważ w pewnych przedziałach x \left| x-2 \right|=-\left( x-2 \right)=-x+2=2-x. Odpowiedź \ln \left( 2-x \right) jest zastrzeżona właśnie do tych przedziałów.
A całkowania jako takiego nauczysz się najlepiej z mojego Kursu Całek Nieoznaczonych , w którym powoli pokazuję i tłumaczę, jak liczyć całki na konkretnych przykładach.




17 Komentarzy
Paula
Hej moglbys mi rozpisac jak obliczyc calke 1/cosx bo mam problem i mi wychodzi kompletnie cos innego . Z góry dziekuje i pozdrawiam
Krystian Karczyński
Przykład wygląda na prosty, a naprawdę to wymaga wyciągnięcia dosyć ciężkiej artylerii, czyli np. „podstawień uniwersalnych”, które pokazałem tutaj.
Jedziemy. Podstawienia biorę sobie z tabelki.
Na tą całkę mamy już gotowy wzór:
KONIEC
Całą metodę na innych przykładach pokazuję w moim Kursie Całki Nieoznaczone, zapraszam!
Dawid
Witam
Mam prośbę nie wychodzi mo to zadanie czy może mi Pan pomóc
całka( 4- 2x)^2 xdx
Joanna Grochowska
Chodzi o całkę: \displaystyle \int{{{{{(4-2x)}}^{2}}xdx}}
Rozpisuję wzór skróconego mnożenia oraz porządkuję wyrażenie pod całką, a same całki wyliczam z wzoru
\displaystyle \int{{{{x}^{n}}dx=\frac{1}{{n+1}}{{x}^{{n+1}}}}}+C
\displaystyle \int{{{{{(4-2x)}}^{2}}xdx}}=\int{{(16-2\cdot 4\cdot 2x+4{{x}^{2}})\cdot xdx=}}\int{{\left( {16x-16{{x}^{2}}+4{{x}^{3}}} \right)dx=}}
\displaystyle 16\int{{xdx-16\int{{{{x}^{2}}dx}}+4\int{{{{x}^{3}}}}dx=}}16\cdot \frac{1}{2}{{x}^{2}}-16\cdot \frac{1}{3}{{x}^{3}}+4\cdot \frac{1}{4}{{x}^{4}}+C=
\displaystyle 8{{x}^{2}}-\frac{{16}}{3}{{x}^{3}}+{{x}^{4}}+C
Edyta
A jaki będzie wynik
a) całka xe^-x dx
b)całka 2x ln x dx
Szymon
pierwsze e^-x*(-x-1) a 2 policz sobie przez czesci.
Kalina
A całka z |1-x| w granicach od 0 do 2? Czy jest równa 1?
Krystian Karczyński
Napisałem posta na ten temat, zapraszam:
Jak poradzić sobie z wartościami bezwzględnymi w całkach (i nie tylko)
Piotr
A to akurat proste podstawiasz w zależności od wartości granicy do właściwego wzoru
pati
od 2 do 0
Krystian Karczyński
A przypadkiem nie od -2 do 0 ?
Karol
Mam pytanie: jak obliczyć całkę z x+1 i to wszystko w wartości bezwzględnej?
Krystian Karczyński
Dobre pytanie, rozumiem, że chodzi tu o całkę nieoznaczoną \int{\left| x+1 \right|dx}?
No więc postępować trzeba tak jak w szkole średniej: rozbić zadanie na dwa przypadki.
1 przypadek – wyrażenie, z którego liczona jest wartość bezwzględna jest większe lub równe zero:
x+1\ge 0, czyli dla x\ge -1
W tym przedziale i dla tych x-sów:
\int{\left| x+1 \right|dx}=\int{\left( x+1 \right)dx}=\int{xdx}+\int{dx}=\frac{1}{2}{{x}^{2}}+x+C
2 przypadek – wyrażenie, z którego liczona jest wartość bezwzględna jest mniejsze od zera:
x+1<0, czyli dla x<-1
W tym przedziale i dla tych x-sów:
\int{\left| x+1 \right|dx}=\int{\left[ -\left( x+1 \right) \right]dx}=-\int{xdx}-\int{dx}=-\frac{1}{2}{{x}^{2}}-x+C
Podsumowując, wynikiem jest rodzina funkcji pierwotnych:
\int{\left| x+1 \right|dx}=\{ \begin{matrix}
& -\frac{1}{2}{{x}^{2}}-x+C\quad dla x<-1 \\
& \frac{1}{2}{{x}^{2}}+x+C\quad dla x\ge -1 \end{matrix}
pati
a jak bedzie to calka oznaczona?
Krystian Karczyński
A w jakich granicach?
Piotr
Całość (tę na dole) można pomnożyć razy sgn(x-1).
Jerzy
Czy mógłby Pan wytłumaczyć, jak obliczyć całkę (1+cos(x)^2)^(0.5) długość łuku sinusoidy?