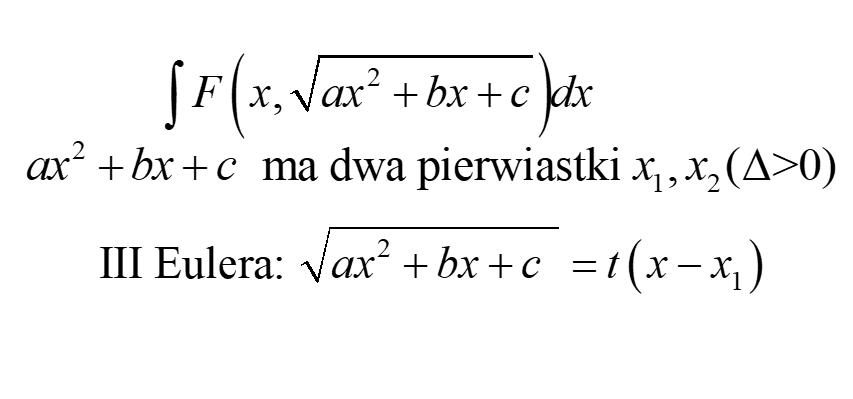
Podstawienia Eulera III rodzaju – Podsumowanie

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka koło Szczecina. Lubi spacery po lesie, plażowanie i piłkę nożną.

Podstawienia Eulera I, II, III rodzaju – Więcej Już Nie Trzeba

W poprzednich postach pokazałem jak stosować podstawienia Eulera w całkach typu:

• Podstawienia Eulera I rodzaju (gdy a>0)
• Podstawienia Eulera II rodzaju (gdy c>0)

W tym poście zajmiemy się trzecim i ostatnim rodzajem podstawień Eulera, które możemy stosować, gdy w całce:

trójmian kwadratowy , ma dwa różne pierwiastki , czyli kiedy jego , czyli kiedy można go zapisać w postaci iloczynowej: .

Zanim jednak przejdziemy do rzeczy, zauważmy, że te trzy przypadki:

• I rodzaj, gdy a>0
• II rodzaj, gdy c>0
• III rodzaj gdy są dwa różne pierwiastki

pozwolą nam rozwiązać każdą całkę typu:

Właściwie nawet tylko I i III rodzaj wystarczą.

Dlaczego?

Przypadek, gdy możemy pominąć, bo trójmian kwadratowy zmienia się po prostu w postać liniową , którą rozwiążemy prostszymi podstawieniami, niż Eulera.

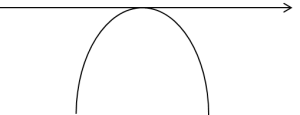
Co jednak z przypadkiem, gdy a<0 (nie pasuje do I rodzaju) i trójmian kwadratowy ma jeden lub w ogóle nie ma pierwiastków (nie pasuje do III rodzaju)?

Wtedy jego wykres wyglądał by tak (pamiętamy ze średniej – ramiona w dół):

albo, jeśli w ogóle nie miałby pierwiastków, tak:

Jaki z tego morał? Że w obu przypadkach trójmian kwadratowy przyjmował by wartości ujemne (z wyjątkiem, co najwyżej jednego punktu), a przypominam, że liczymy całkę:

Czyli, że w funkcji podcałkowej trójmian kwadratowy jest pod pierwiastkiem, a ten nie może być liczony z wartości ujemnych (bawimy się w liczby rzeczywiste, oczywiście). Czyli dziedziną takiej funkcji byłby co najwyżej jeden punkt, czyli że w ogóle bez sensu i takiego przykładu na pewno nie dostaniemy. Chyba, że Pan profesor będzie naprawdę niewyspany przy układaniu przykładów na kolokwium.

Przypadek więc, gdy a<0 i trójmian nie ma dwóch pierwiastków można pominąć i teraz wyraźnie widać, że I i III rodzaj podstawień Eulera pasuje do KAŻDEJ całki typu:

Do rzeczy zatem, bierzmy się za III rodzaj podstawień Eulera.

Podstawienia Eulera III rodzaju

Mamy całkę:

, w której ma , czyli można go zapisać jako:

, gdzie to jego pierwiastki.

Podstawienie, jakie tu stosujemy, to:

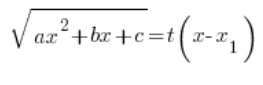
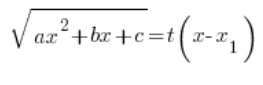
Podstawienie to podnosimy obustronnie do kwadratu, trójmian po lewej stronie zapisujemy w postaci iloczynowej (wiemy, że można), dzielimy obie strony przez i dalej, tak jak w poprzednich rodzajach podstawień, wyznaczamy w kolejności:

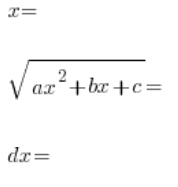
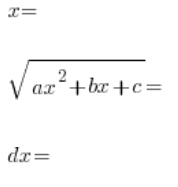
Na końcu podstawiamy całość do całki wyjściowej i wychodzimy na – z reguły żmudną – całkę wymierną.

Do dzieła.

Przykład

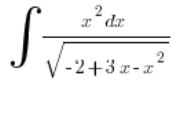
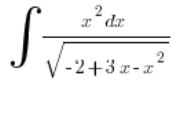
Nasze (czyli a<0, czyli nie zastosujemy podstawień I rodzaju), nasze (czyli c<0, czyli nie zastosujemy podstawień II rodzaju), ale za to nasza , czyli możemy zastosować podstawienia III rodzaju.

Liczymy na początku :

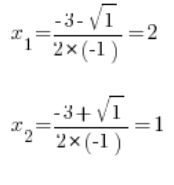
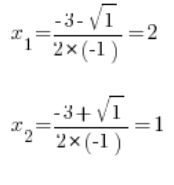
Stosujemy podstawienie Eulera III rodzaju:

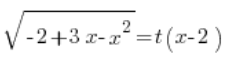
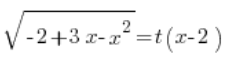
Podnosimy obie strony do kwadratu:

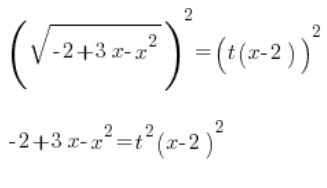
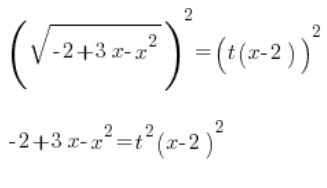
Trójmian po lewej zapisujemy w postaci iloczynowej (pamiętać o    mi tutaj!!!):

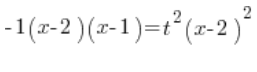
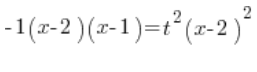
Dzielimy obustronnie przez :

   /:

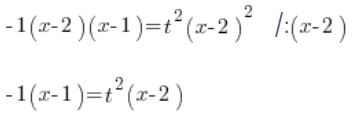
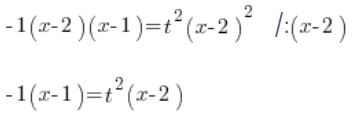
Wyznaczamy :

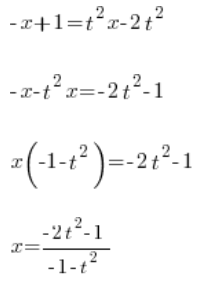
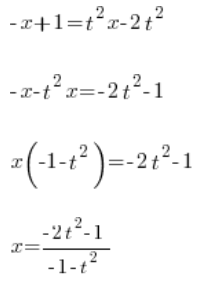
Mamy    wyznaczone przy pomocy zmiennej . Teraz bierzemy się za wyznaczenie .

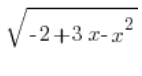
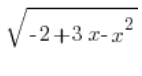
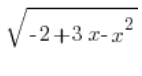
Wracając się do naszego pierwszego podstawienia mamy, że:

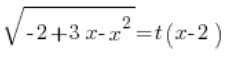
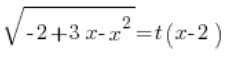
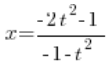
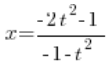
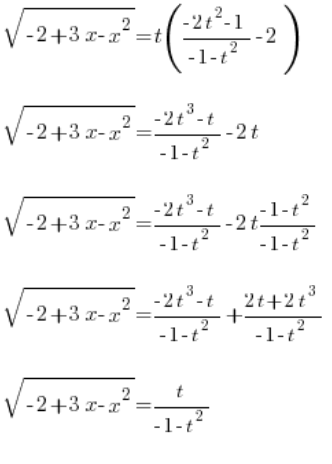
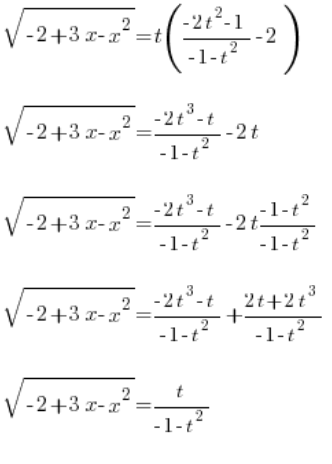
Wstawiamy wyznaczone i mamy:

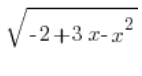
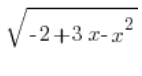
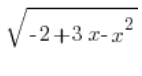
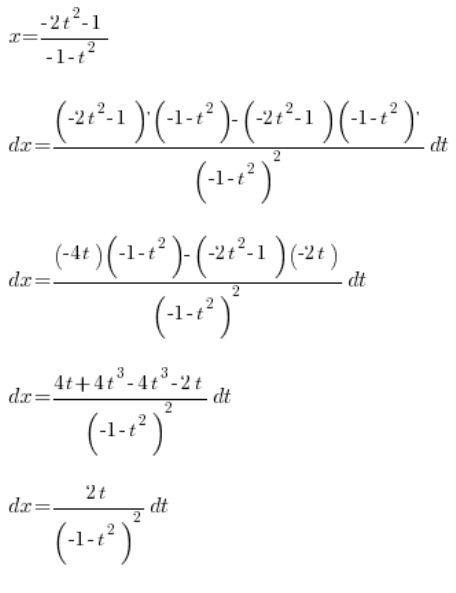
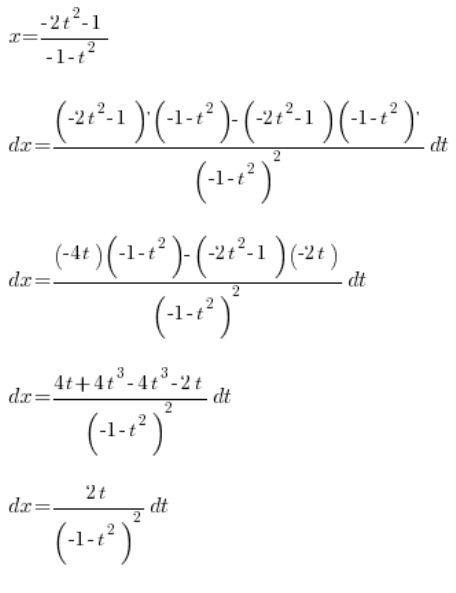
Mamy całkiem zgrabnie wyznaczone  . Teraz już tylko , które policzymy licząc pochodną z :

Mamy więc wyznaczone:

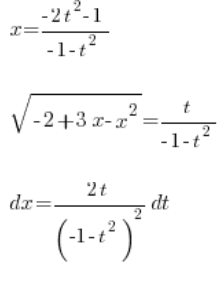
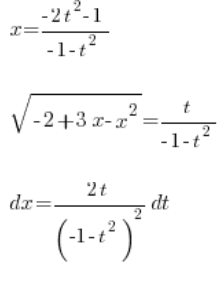
, wszystko przy pomocy zmiennej  . Wrzucamy to do całki:

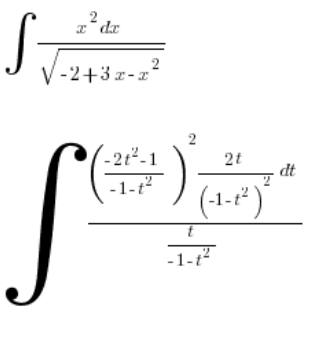
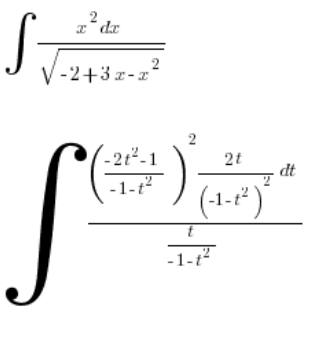
Upraszczamy:

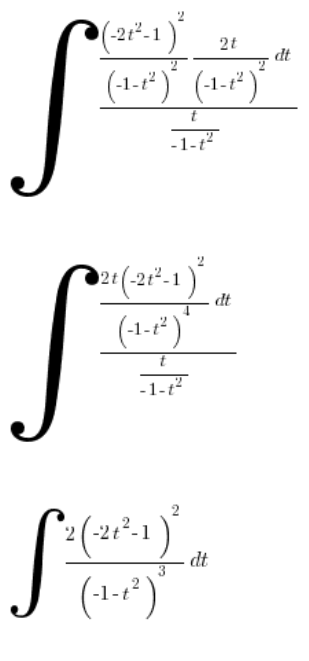
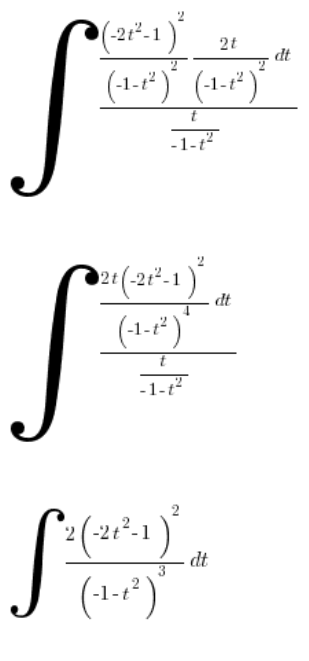
Zgodnie z przewidywaniami wychodzimy na naprawdę już mocną całkę wymierną, której obliczanie sobie odpuszczam.

Na koniec warto jeszcze zauważyć, że…

Uwaga odnośnie podstawień Eulera

Mając całkę:

, w której:

• I rodzaj, gdy a>0
• II rodzaj, gdy c>0
• III rodzaj gdy są dwa różne pierwiastki

, oczywistym jest, że często można będzie ją rozwiązywać jednym z dwóch podstawień Eulera, albo nawet dowolnym z nich (kiedy a>0, c>0 i jednocześnie ).

Żaden problem, choć ze względu na łatwość obliczeń polecał bym stosować w pierwszej kolejności I rodzaj, jak się nie da, to II, a jak się nie da, to dopiero III.

Tyle o stosowaniu podstawień Eulera, mam nadzieję, że przyda to Wam się na studiach, jak zawsze zapraszam do komentarzy pod postem.