fbpx
blog
Brak komentarzy Dołącz do dyskusji

Co podniesione do kwadratu daje 17? Czyli całki nieoznaczone i wzór z arctgx

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Wzór z arctgx w typowych sytuacjach

Przyzwyczailiśmy się do stosowania wzoru: int{ }{ }{dx/{x^2+a^2}}=1/a{arctg{x/a}+C} w “czystych” sytuacjach całkowych,

takich jak:

int{ }{ }{dx/{x^2+1}}

int{ }{ }{dx/{x^2+4}}

int{ }{ }{dx/{x^2+9}}

int{ }{ }{dx/{x^2+16}}

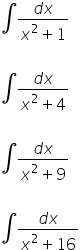
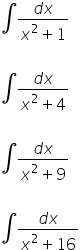
Przekształcamy wtedy prosto…

int{ }{ }{dx/{x^2+1}}=int{ }{ }{dx/{x^2+1^2}}

int{ }{ }{dx/{x^2+4}}=int{ }{ }{dx/{x^2+2^2}}

int{ }{ }{dx/{x^2+9}}=int{ }{ }{dx/{x^2+3^2}}

int{ }{ }{dx/{x^2+16}}=int{ }{ }{dx/{x^2+4^2}}

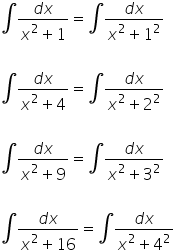
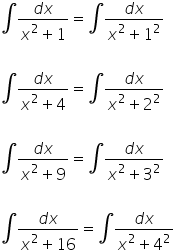
…i wychodzimy elegancko na wynik:

int{ }{ }{dx/{x^2+1}}=int{ }{ }{dx/{x^2+1^2}}=1/1{arctg{x/1}}+C

int{ }{ }{dx/{x^2+4}}=int{ }{ }{dx/{x^2+2^2}}=1/2{arctg{x/2}}+C

int{ }{ }{dx/{x^2+9}}=int{ }{ }{dx/{x^2+3^2}}=1/3{arctg{x/3}}+C

int{ }{ }{dx/{x^2+16}}=int{ }{ }{dx/{x^2+4^2}}=1/4{arctg{x/4}}+C

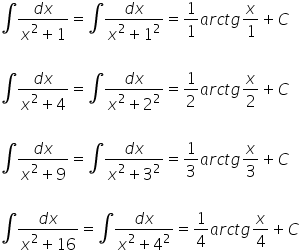
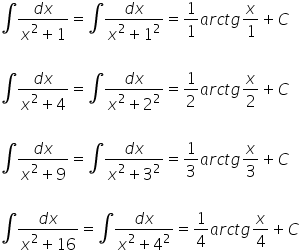
Wzór z arctgx w sytuacjach nietypowych

A co zrobić z taką całką nieoznaczoną:

int{ }{ }{dx/{x^2+17}} ? Co podniesione do kwadratu daje 17? Nic? Nieee…. sqrt{17} podniesione do kwadratu daje 17, zatem:

int{ }{ }{dx/{x^2+17}}=int{ }{ }{dx/{x^2+(sqrt{17})^2}}=1/sqrt{17}{arctg{x/sqrt{17}}}+C

Ogólnie rzecz biorąc więc, wzorem int{ }{ }{dx/{x^2+a^2}}=1/a{arctg{x/a}+C} obsłużymy każdą całkę nieoznaczoną tego typu, stałe w mianowniku nie muszą być takie łatwe do przedstawienia jako coś do kwadratu…

Jedna z wielu opinii o naszych Kursach...

Jestem zadowolony z kursu. Logika zaliczona. Do łba przez prawie miesiąc nic nie nie wchodziło a tu raptem w trakcie kursu doznałem olśnienia. Dodam, iż dokonałem jego zakupu dwa dni przed ogłoszeniem wyroku i to wystarczyło, aby go odroczyć – mam nadzieję, że na zawsze. Teraz studiuję pozostałe kursy i patrzę jasno w przyszłość. Polecam go każdemu a w szczególności tym koleżankom i kolegom, którzy uważają, że wszystko jest stracone.

Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?

Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.

Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany. Wymagane pola są oznaczone *

Twój komentarz będzie dostępny publicznie na naszej stronie razem z powyższym podpisem. Komentarz możesz zmienić, lub usunąć w każdej chwili. Administratorem danych osobowych podanych w tym formularzu jest eTrapez Usługi Edukacyjne E-Learning Krystian Karczyński. Zasady przetwarzania danych oraz Twoje uprawnienia z tym związane opisane są w Polityce Prywatności.


blog

Nowy Kurs z Fizyki dla studentów – Mechanika Płynów

02 stycznia 2023 / Jan Rychlewski

Czytaj więcej
blog

Wprowadzenie do granic ciągów. Wyciąganie przed nawias najwyższej potęgi. Pełna DARMOWA Lekcja Kursu Granice [VIDEO]

13 stycznia 2022 / Krystian Karczyński

Czytaj więcej
blog

Elementy kombinatoryki: reguła mnożenia, permutacje, wariacje, kombinacje. Pełna darmowa Lekcja Kursu Prawdopodobieństwo. [VIDEO]

03 stycznia 2022 / Krystian Karczyński

Czytaj więcej