Pochodne Funkcji Wykład 4
Temat: Badanie istnienia pochodnej – przykłady
Streszczenie
Wykład poświęcony będzie kilku konkretnym zadaniom, w którym wykazywać będziemy istnienie (lub nie) pochodnej funkcji w punkcie, korzystając z wiadomości z poprzedniego wykładu.
Przykład 1
Sprawdź istnienie pochodnej z funkcji f(x) w punkcie ![]() :
:
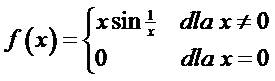
Jak widzieliśmy w poprzednim wykładzie, aby zbadać istnienie pochodnej tej funkcji w punkcie 0 należy zbadać istnienie pochodnej lewo i prawostronnej z funkcji w tym punkcie.
Zaczynamy od pochodnej lewostronnej:
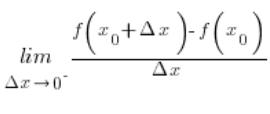
Za ![]() podstawiamy zero i mamy:
podstawiamy zero i mamy:
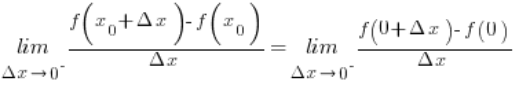
![]() z naszego wzoru na funkcję i mamy:
z naszego wzoru na funkcję i mamy:
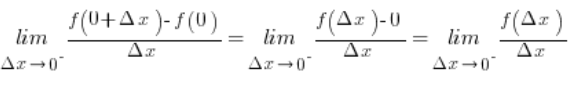
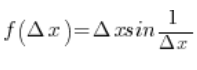 z naszego podstawowego wzoru na funkcję (bo \Delta x\ne 0), zatem:
z naszego podstawowego wzoru na funkcję (bo \Delta x\ne 0), zatem:
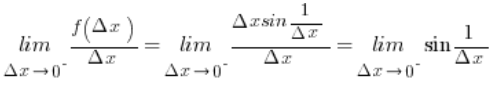
Jeżeli ![]() mamy więc granicę z sinus z czegoś rozbiegającego w
mamy więc granicę z sinus z czegoś rozbiegającego w ![]() , a taka granica w ogóle nie istnieje (pokazałem to w jednym z moich postów na blogu).
, a taka granica w ogóle nie istnieje (pokazałem to w jednym z moich postów na blogu).
Zatem pochodna lewostronna funkcji f(x) w punkcie ![]() NIE ISTNIEJE.
NIE ISTNIEJE.
Całe rozumowanie moglibyśmy powtórzyć właściwie dla pochodnej prawostronnej.
Zatem funkcja f(x) nie ma w punkcie ![]() pochodnej ani lewo, ani prawostronnej. Pochodna tej funkcji w tym punkcie nie istnieje (mimo, że można pokazać, iż funkcja w tym punkcie jest ciągła).
pochodnej ani lewo, ani prawostronnej. Pochodna tej funkcji w tym punkcie nie istnieje (mimo, że można pokazać, iż funkcja w tym punkcie jest ciągła).
Przykład 2
Sprawdź istnienie pochodnej z funkcji f(x) w punkcie ![]() :
:
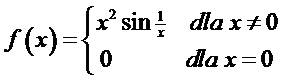
Badamy istnienie pochodnych jednostronnych, zaczynając od pochodnej lewostronnej:
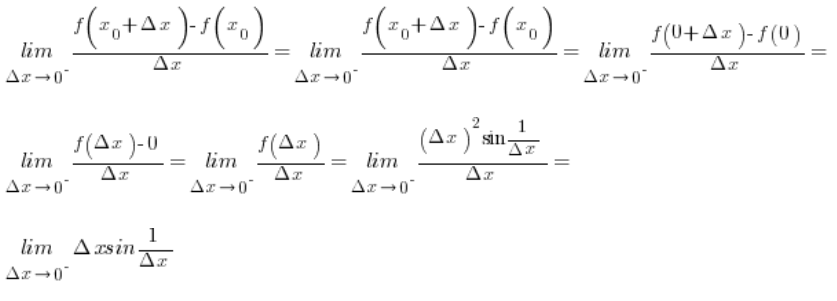
Przy pomocy twierdzenia o trzech funkcjach (sprawdź odpowiedni post na moim blogu) można pokazać, że granica tej funkcji istnieje i jest równa zero. Rzeczywiście, zachodzi nierówność:
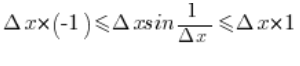
Granica zaś z funkcji ograniczającej z dołu i funkcji ograniczającej z góry jest równa 0:
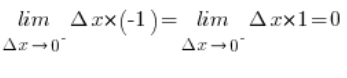
Zatem na mocy twierdzenia o trzech funkcjach:
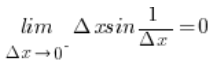
Pochodna lewostronna zatem istnieje i jest równa 0.
Całe rozumowanie można powtórzyć dla pochodnej prawostronnej, która również równa będzie 0.
Zatem pochodna funkcji f(x) w punkcie 0 istnieje i jest równa 0.
Przykład 3
Oblicz pochodne jednostronne z funkcji ![]() w punkcie
w punkcie ![]() .
.
Zaczynamy od pochodnej lewostronnej:
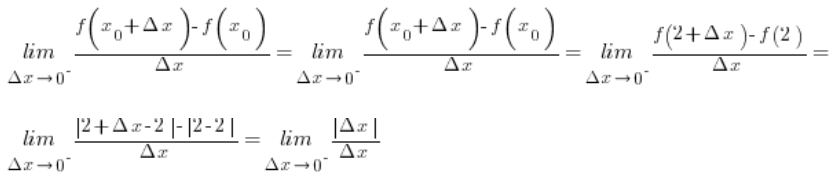
![]() jest ujemna (bo
jest ujemna (bo ![]() ), zatem:
), zatem:
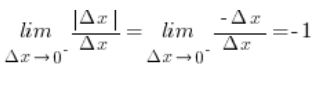
Zatem pochodna lewostronna funkcji f(x) w punkcie 2 jest równa -1.
Teraz liczymy pochodną prawostronną:
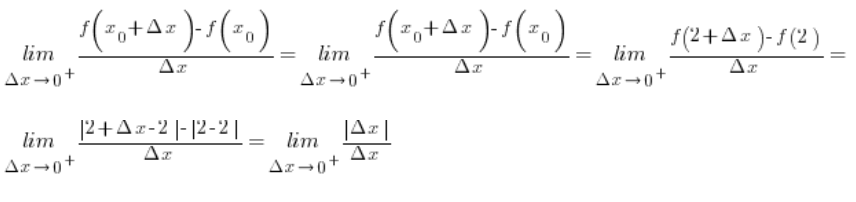
![]() jest dodatnia (bo
jest dodatnia (bo ![]() ), zatem:
), zatem:
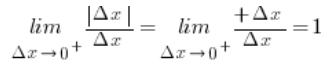
Czyli pochodna prawostronna z funkcji f(x) w punkcie 2 jest równa 1.
Przykład 4
Sprawdź istnienie pochodnej z funkcji 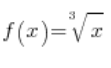 w punkcie
w punkcie ![]() .
.
Tu zauważmy bardzo ciekawą rzecz. Pochodna z funkcji f(x) obliczona wzorami równa była by 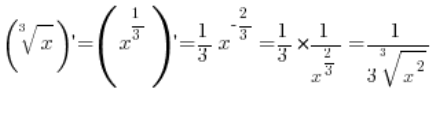 .
.
Jednak pochodna obliczona tym wzorem w punkcie ![]() nie istnieje (ten punkt nie należy do jej dziedziny). Zatem nie możemy zastosować tego wzoru w punkcie
nie istnieje (ten punkt nie należy do jej dziedziny). Zatem nie możemy zastosować tego wzoru w punkcie ![]() i musimy badać w nim pochodną z definicji.
i musimy badać w nim pochodną z definicji.
Zaczynamy od pochodnej lewostronnej:
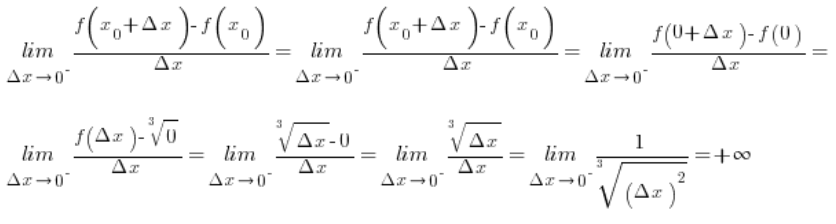
Ten sam wynik zostanie osiągnięty przy obliczaniu pochodnej prawostronnej (w mianowniku ![]() jest zawsze dodatnie, bo podniesione do kwadratu).
jest zawsze dodatnie, bo podniesione do kwadratu).
Zatem funkcja f(x) ma w punkcie 0 pochodną nieskończoną ![]() .
.
KONIEC
Pisząc tego posta korzystałem z…
1. „Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.
Kliknij, aby przypomnieć sobie, jak obliczać pochodne jednostronne funkcji (poprzedni Wykład) <–
Kliknij, aby przejść do wzorów na pochodne funkcji (następny Wykład) –>

