الاقتصاد القياسي – المحاضرة 7
الموضوع: الطريقة الكلاسيكية للمربعات الصغرى – الافتراضات
ستُخصَّص هذه المحاضرة للطريقة الكلاسيكية للمربعات الصغرى. قد تَصادف أيضًا اسم النموذج الكلاسيكي للانحدار الخطي (KMRL). كلا الاسمين صحيحان ويمكنك استخدامهما بحرية.
سأعرض لك وأناقش بإيجاز جميع الافتراضات الأساسية لهذه الطريقة. وهي تتعلق أساسًا بخصائص معينة للمكوّن العشوائي.
من المهم معرفة هذه الافتراضات، لأنها غالبًا ما تظهر في امتحان الاقتصاد القياسي، وليس فقط. أتذكر جيدًا أن ذكر افتراضات KMNK كان أحد الأسئلة في دفاعي عن مشروع التخرج 🙂
إذن، أدعوك للمتابعة!
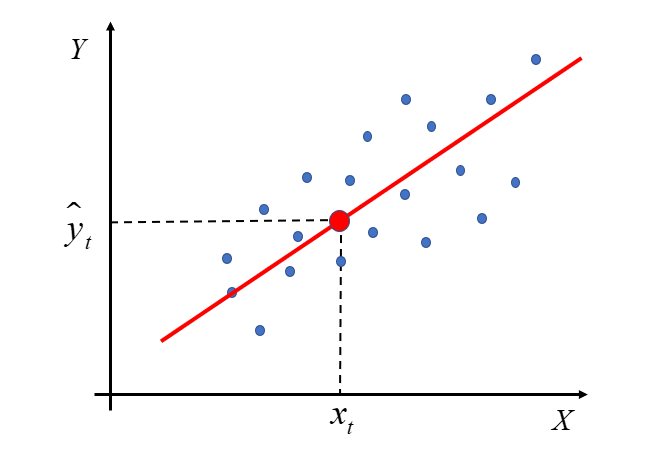
لنبدأ من البداية، أي من الاسم نفسه. في المحاضرة السابقة تمت مناقشة طريقة المربعات الصغرى. جوهرها يظهر بشكل أوضح في مثال نموذج بمتغيرين – المتغير التابع Y والمتغير المستقل X. الطريقة الكلاسيكية للمربعات الصغرى هي ببساطة تسمية لجميع الشروط اللازمة لتطبيق طريقة المربعات الصغرى لتقدير متجه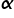 
في النموذج:
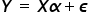
هنا سأقوم بتفصيل افتراضات الطريقة الكلاسيكية للمربعات الصغرى. هذه الافتراضات مهمة جدًا، لأنه فقط عند تحققها – أي عندما تتصف البيانات الفعلية المستخدمة في النموذج الاقتصادي بهذه الخصائص – يمكن حينها بناء النموذج وتطبيق طريقة المربعات الصغرى لتقدير معلمات النموذج.
بالطبع، هناك طرق أخرى لتقدير معلمات النموذج، ولكل منها “إرشاداتها” الخاصة، مثل: الطريقة المعممة للمربعات الصغرى (UMNK)، طريقة الاحتمالية العظمى (MNW)، طريقة الانحدار الثنائي، إلخ.
افتراضات KMNK هي كما يلي:
- النموذج الاقتصادي المُقدَّر خطي بالنسبة للمعلمات
. - المتغيرات المستقلة ثابتة وغير عشوائية.
- رتبة مصفوفة تساوي عدد المعلمات المقدَّرة، أي .
- حجم العينة أكبر من عدد المعلمات المقدَّرة، أي .
- لا يوجد ارتباط خطي تام (تعدد خطي) بين المتغيرات المستقلة.
- القيمة المتوقعة للمكوّن العشوائي تساوي الصفر: لكل t.
- للمكوّن العشوائي تباين ثابت ومحدود: .
- لا يوجد ارتباط ذاتي (Autocorrelation) بين المكونات العشوائية، أي لكل t ≠ s.
- المكوّن العشوائي يتبع توزيعًا طبيعيًا متعدد الأبعاد من الدرجة n: لكل t = 1, 2, …, n.
لاحظ أن عددها كبير.
قد تكون قد رأيت في محاضراتك عددًا أقلّ منها مذكورًا صراحة. على سبيل المثال، الافتراض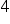 
و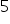
يترتّبان على الافتراض رقم 
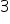، ولذلك قد يتمّ تجاوزهُما. كثيرًا ما تُدمج آخر أربعة افتراضات الخاصة بالمكوّن العشوائي في نقطة فرعية واحدة.
سأحاول الآن توضيح معنى كلّ افتراض بمزيد من التفصيل.
الافتراض 1. النموذج الاقتصادي المُقدَّر خطي بالنسبة للمعلمات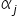 
.
في أحد المقالات السابقة شرحتُ متى يكون النموذج الاقتصادي خطيًا بالنسبة للمعلمات ومتى يكون خطيًا بالنسبة للمتغيرات. ما يهمّنا هنا هو الخطية بالنسبة للمعلمات المجهولة .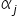
عمومًا، في النموذج الخطي المعتاد تلعب صيغة مجموع المضروبات من النوع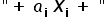 
الدورَ الرئيسي. وهذا يعني أن تكون المعلمات وكذلك المتغيرات في القوى الأولى، وأن يكون المتغير التابع Y تركيبًا خطيًا للمتغيرات المستقلة ولمعاملات مختلفة.
ومن ثمّ يمكن كتابة هذا النموذج في صورة مصفوفية: .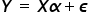
المتجه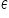 
هو متجه المكوّنات العشوائية (المشاهدات الفردية) التي تمثّل التأثير الإجمالي لجميع العوامل الثانوية والعرضية غير المضمنة ضمن المتغيرات المستقلة. إن إضافة متجه الاضطرابات العشوائية 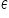إلى الجزء الحتمي من النموذج يهدف إلى تمثيل حقيقة أن المشاهدات المسجّلة قد تختلف في قيمها عن القيم الناتجة عن البنية النظرية للنموذج الاقتصادي. يجمع المتجه 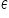مكوّنات عشوائية غير قابلة للرصد بطبيعتها؛ نفترض وجودها لشرح أي فروق بين القيم النظرية للمتغير التابع والقيم المرصودة. نظريًا، إذا كنّا نعرف عدد المتغيرات المستقلة المهمة (k) ونعرف شكل العلاقة (خطي)، أي إذا كان Z1 محققًا، فـ ε يشتمل فقط على عوامل عرضية وثانوية ومشوِّشة. أمّا عمليًا فعلينا أن نضع في الحسبان أنّ المكوّن العشوائي يضمّ أيضًا تبعات الأخطاء الآتية:
1. خطأ المواصفة (إهمال متغير مهم، إدراج متغير غير مهم، إلخ).
2. خطأ التقريب (إذا كان شكل العلاقة مختلفًا، كأن يكون غير خطي بدرجة جوهرية، ولا يُقَرَّب جيدًا بالشكل الخطي).
عمليًا نفترض أن Z1 ليس متحققًا على نحوٍ مثالي (لكن يمكننا الافتراض أننا اخترنا المتغيرات المستقلة جيدًا وأن الشكل الحقيقي للعلاقة يُقَرَّب جيدًا بعلاقة خطية…). ستُوصَف خصائص 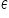بمزيد من التفصيل في البنود Z6–Z9.
الافتراض 2. المتغيرات المستقلة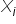 
هي كميات غير عشوائية ذات عناصر محددة.
المتغيرات المستقلة غير عشوائية. وتُعامَل قيمها كثوابت عبر العينات المكرَّرة.
المعلومات الواردة في العيّنة هي المصدر الوحيد الذي تستند إليه عملية تقدير معلمات البنية في النموذج.
الإخلال بهذا الافتراض يؤدّي إلى فقدان خصائص مهمة للمقدِّرات.
الافتراض 3. رتبة المصفوفة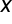 
تساوي عدد المعلمات المقدَّرة، أي 
.
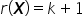رتبة المصفوفة هي عدد الأعمدة المستقلة خطيًا. ويمكن القول أيضًا إنها عدد الصفوف المستقلة خطيًا. غير أنه في التعبير المصفوفي تمثل الصفوفُ المشاهداتِ المتعاقبة، بينما تمثل الأعمدةُ المتغيراتِ المستقلة 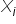. لذلك المقصود هنا هو الاستقلالية بين المتغيرات المستقلة.
تضمن هذه الافتراضات إمكانية تحديد المقدِّر بشكل وحيد.
وينتج عن الافتراض 3 مباشرةً الافتراضان 4 و5. ولهذا يُتجاوَز أحيانًا ذكرهما على نحو منفصل.
الافتراض 4. حجم العيّنة أكبر من عدد المعلمات المقدَّرة، أي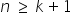 
.
يجب أن يكون عدد المشاهدات n أكبر من عدد المعلمات المقدَّرة (المتغيرات المستقلة).
الافتراض 5. لا يحدث تواطؤ خطي (تعدد خطي/توازي خطي) بين المتغيرات المستقلة
لا يجوز أن تكون المتغيرات المستقلة متوازية خطيًا؛ أي يجب أن تكون متجهات مشاهدات المتغيرات المستقلة (أعمدة مصفوفة X) مستقلة خطيًا.
للمكوّن العشوائي خصائص محددة ينبغي تحققها ضمن هذا الافتراض.
سلوك المكوّن العشوائي في النموذج القياسي بصورته العامة يُعدّ من أهم مصادر المعرفة حول ما إذا كان النموذج قد بُني بطريقة صحيحة.
قيمته هي الفرق بين القيمة التجريبية في الفترة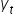 
والقيمة النظرية المُقدَّرة بناءً على قيم المتغيرات المستقلة في الفترة نفسها.
بحسب التعريف، النموذج (بالمعنى الواسع) هو تمثيل مبسّط للواقع. وعليه، فعند بناء نموذج قياسي نرغب في “تبسيط” بعض الظواهر الاقتصادية إلى صيغة دالّة. وفي الوقت نفسه نتوقع أن يعكس النموذج الواقع بأفضل شكل ممكن؛ أي أن يكون الفرق بين القيمة التي حدثت فعليًا (التجريبية) وبين ما حسبناه وفقًا للنموذج (النظرية) صغيرًا قدر الإمكان، أي قريبًا من الصفر.
تُذكر أدناه خصائص المكوّن العشوائي. وعلى الرغم من أن صياغتها تبدو معقدة، فإن الأمر أيسر مما يبدو.
لنبدأ من أنه لو كان المكوّن العشوائي يتبع نمطًا محددًا، لما أمكن الحديث عن أي “عشوائية” أصلًا. وهذا يعني أن هناك «شيئًا يحدث» داخل البواقي، وأن النموذج لم يُبنَ على نحو صحيح. وبما أننا نرى وجود نمط ما، فيلزمنا الكشفُ عمّا يكمن هناك. على الأرجح، عندما تظهر الارتباطات الذاتية في قيم المكوّن العشوائي، يكون ثمة عامل ذو تأثير كبير في تشكيل المتغير التابع لم نأخذه بالحسبان عند التفكير في العوامل المؤثرة في المسألة المدروسة. ومن الطرق السريعة المتبعة لخفض معامل الارتباط الذاتي إضافةُ متغير داخلي متأخر زمنيًا إلى النموذج، لكن هذا موضوع أكثر تعقيدًا وسنتركه لوقت لاحق.
الافتراض 6. القيمة المتوقعة للمكوّن العشوائي تساوي صفرًا: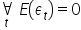 
.
القيم المتوقعة لمكوّنات العشواء تساوي الصفر (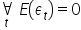 لكل t = 1, 2, …, n). هذا يعني أن الاضطرابات التي تمثلها المكوّنات العشوائية تميل إلى تعويض بعضها بعضًا.
الافتراض 7. للمكوّن العشوائي تباين ثابت ومحدود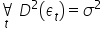 
.
تكون تباينات المكوّنات العشوائية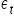 
ثابتة، أي 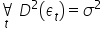لكل t = 1, 2, …، n. وهذه تُعرف بخاصية «تجانس التباين» (Homoskedasticity).
مصفوفة التباينات والتقاربات بين بواقي المكوّنات تكون على الصورة
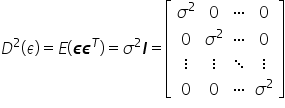
يضمن هذا الافتراض أن قيمة تباين الاضطرابات لا تعتمد على رقم المشاهدة.
الافترضان 6 و7 يحددان الخصائص المرغوبة لمقدِّر المتجه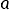 
لمعلمات المتجه 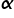، ولكن الحديث عن ذلك سيكون في المحاضرة التالية.
الافتراض 8. لا يحدث الارتباط الذاتي للمكوّن العشوائي، أي لا توجد علاقة بين المكوّن العشوائي في وحدات زمنية مختلفة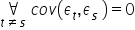 
.
المكوّنان العشوائيان 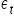و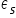
مستقلان عن بعضهما. أي لا يوجد ما يُسمّى بالارتباط الذاتي للمكوّنات العشوائية.
وهذا يعني وجود علاقة خطية بين بواقي النموذج المتباعدة بمقدار “k” من الفترات. وهذا يخصّ النماذج الديناميكية.
وظهوره يدل على أنه تمّ إغفال أحد المتغيرات المستقلة المهمة في النموذج أو أنه تمّ اعتماد صيغة غير مناسبة للنموذج.
الافتراض 9. للمكوّن العشوائي توزيع طبيعي بُعدُه n: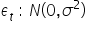 
لكل t = 1, 2, …, n.
كل مكوّن عشوائي 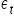يتبع توزيعًا طبيعيًا.
هذا الافتراض المتعلق بطبيعية توزيع المكوّن العشوائي مهمّ عند إجراء الاستدلال الإحصائي.
إذا تبيّن أن الافتراضات الأربعة أعلاه صادقة في النموذج الذي نحلّله، فيمكننا فهم المكوّنات المشوِّشة على أنها ناتجة عن عملية الضجيج الأبيض. في هذه الحالة ستكون جميع معاملات الارتباط الذاتي ومعاملات الارتباط الذاتي الجزئي معدومة وغير دالّة إحصائيًا. ولتحديد ما إذا كان هناك ضجيج أبيض، لا بدّ من إجراء اختبارات الفرضيات المناسبة. ومن بينها مثلًا إحصائية كوينويل (Quenouille) وإحصائية دوربين–واتسون.
في المحاضرة أعلاه حاولتُ تقريب افتراضات الطريقة الكلاسيكية للمربعات الصغرى إليك.
في الواقع، كان ينبغي أن تسبق هذه المحاضرةُ محاضرةَ طريقة المربعات الصغرى، لأن من المنطقي أولًا عرض الافتراضات ثم تطبيق الطريقة واستخراج صيغ مقدِّرات معلمات النموذج .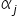
آمل أنه بما أنك تعرف الآن ما هي طريقة المربعات الصغرى وقد تعرّفت إلى افتراضات قابلية تطبيقها، فسيصبح الانحدار الخطي أقرب إليك ولن يبدو مخيفًا 🙂
النهاية
انقر للعودة إلى صفحة محاضرات الاقتصاد القياسي
