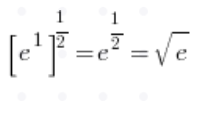الحدود النموذجية للتسلسل مع صيغة للعدد e
المسائل التقليدية على حدود التسلسل مع صيغة للعدد e تؤدي بشكل “طبيعي” إلى الصيغة (أشرح كيف يتم ذلك في دورتي):
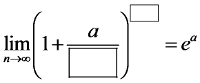لكن ماذا لو لم يكن لدينا هذا الكسر الأنيق في القوس، بل شيء مثل:
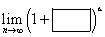إذا كان المستطيل في القوس يتقارب إلى الصفر، والمثلث في الأس يؤدي إلى اللانهاية، لدينا هنا رمز غير محدد 
– يعني بالضبط هذا النوع الذي نستخدم فيه الصيغة مع العدد ‘e’ في النتيجة. ماذا نفعل؟
حسنا، لنتذكر أنه يمكن تمثيل أي تعبير على أنه تقسيم الواحد على مقلوبه 🙂
على سبيل المثال، يمكن كتابة الرقم 2 العادي المهذب كالتالي:
لذا، يمكن تحويل أي تعبير إلى كسر “بالقوة” إذا كان ذلك ضروريا حقا.
مثال على حد غير تقليدي مع صيغة للعدد e
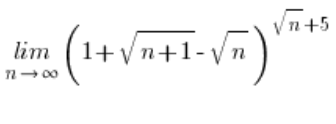
أولا، ينبغي إثبات أن التعبير 
يميل إلى الصفر. يمكنك فعل ذلك بحساب الحد:
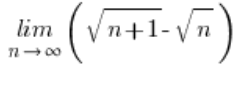– النتيجة ستكون صفر فعلا (يمكنك استخدام طريقة الضرب بالترافق).
الآن، تقوم بتبديل:
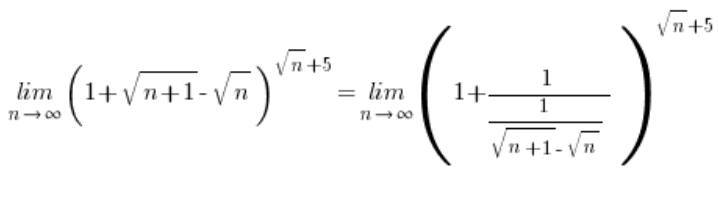
…ثم تستمر وفقا للمخطط المعروف:
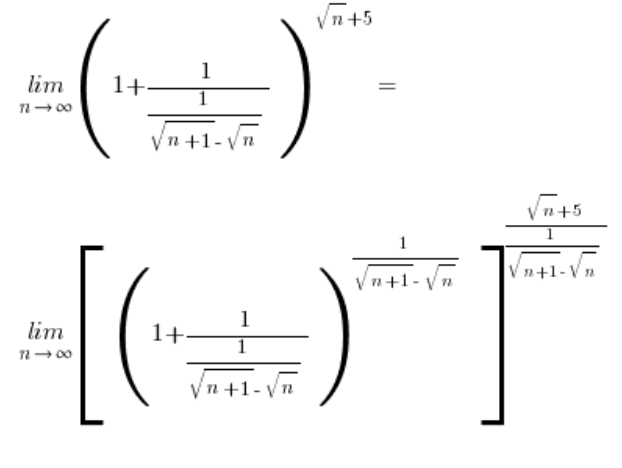
الحد في القوس المربع الكبير يساوي: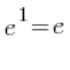 
– وفقا للصيغة الأساسية للحدود، يبقى فقط العمل على:
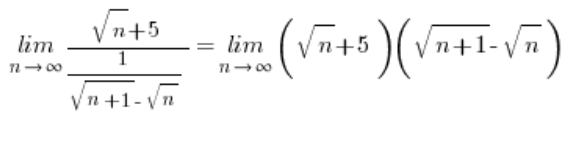
… والتي بعد تطبيق الضرب بالترافق ستنتهي بالنتيجة 
.
وبالتالي فإن الحد كله يساوي:
