Currently Empty: zł0.00
Krystian Karczyński- 2 يوليو 2024
- Comment 0
عند حل مسائل الأعداد المركبة، يجب مراعاة أن العدد المركب في الشكل المثلثي يبدو هكذا:
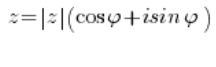
وفقط هكذا. لا أقل، ولا أكثر.
لذلك يجب الانتباه إلى:
متى يكون العدد المركب في الشكل المثلثي ومتى لا يكون؟
- العدد: هو عدد في الشكل المثلثي حيث أن المعيار للعدد يساوي 1 ()، لأنه بالطبع:
- العدد: ليس عدداً في الشكل المثلثي لأن أمام الوحدة التخيلية ‘i’ مضروبة في الجيب يوجد علامة ناقص، بينما يجب أن تكون زائد.
لتحويل هذا العدد إلى الشكل المثلثي، يجب استخدام الصيغ المثلثية:
باستخدام هذه الصيغ، يمكننا تحويل:
الدوال الجيبية والجيب التمام هي-دورية، لذا قيمتها تكون نفسها كـ . كتبت المزيد عن هذا الموضوع في: هذا المنشور.
لدينا في النهاية:
…وهذا هو العدد في الشكل المثلثي. - العدد: ليس عدداً في الشكل المثلثي لأن أمام الوحدة التخيلية ‘i’ مضروبة في الجيب يوجد علامة ناقص، بينما يجب أن تكون زائد، وكذلك أمام الجيب التمام يوجد علامة ناقص، بينما يجب أن تكون زائد.
لتحويل هذا العدد إلى الشكل المثلثي، يجب إخراج الناقص أمام القوس:
تحويل العدد إلى الشكل المثلثي (هذا ما نتقنه الآن…):
إذاً لدينا ضرب عددين في الشكل المثلثي:
ولضرب الأعداد في الشكل المثلثي، نضرب معاييرها ونضيف الحجج (هناك صيغة لذلك)، إذاً لدينا:
وهذا هو العدد في الشكل المثلثي. - العدد: ليس عدداً مركباً في الشكل المثلثي لأن قبل الكوسينوس يوجد علامة ناقص، ويجب أن تكون زائد.
لتحويل هذا العدد المركب إلى الشكل المثلثي، يجب إخراج الناقص قبل القوس:
يجب تحويل العدد -1 إلى الشكل المثلثي (كما فعلنا في النقطة 3)، وكذلك العدد إلى الشكل المثلثي (كما فعلنا في النقطة 2).
سنحصل على:
باستخدام صيغة ضرب الدوال المثلثية:
وباستخدام دورية الدوال الجيبية والكوسينوس:
- العدد: ليس عدداً مركباً في الشكل المثلثي لأن قبل الكوسينوس توجد الوحدة التخيلية ‘i’ (ولا يجب أن تكون هناك)، وقبل الجيب لا توجد الوحدة التخيلية ‘i’.
يجب استخدام الصيغ المثلثية المعروفة من المدرسة الثانوية:
لدينا:
وهذا هو العدد المركب في الشكل المثلثي. - العدد: ليس عدداً مركباً في الشكل المثلثي.
يجب تبديل الجيب بالكوسينوس كما فعلنا في النقطة 5، ثم حلها كما في النقطة 4. - العدد: ليس عدداً مركباً في الشكل المثلثي.
يجب تبديل الجيب بالكوسينوس كما فعلنا في النقطة 5، ثم حلها كما في النقطة 2. - العدد: ليس عدداً مركباً في الشكل المثلثي.
يجب تبديل الجيب بالكوسينوس كما فعلنا في النقطة 5، ثم حلها كما في النقطة 3.
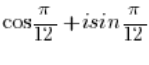هو عدد في الشكل المثلثي حيث أن المعيار للعدد يساوي 1 (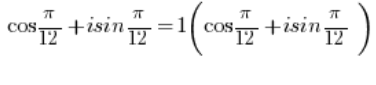
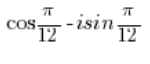)، لأنه بالطبع:
ليس عدداً في الشكل المثلثي لأن أمام الوحدة التخيلية ‘i’ مضروبة في الجيب يوجد علامة ناقص، بينما يجب أن تكون زائد.
-دورية، لذا قيمتها تكون نفسها كـ 
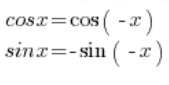
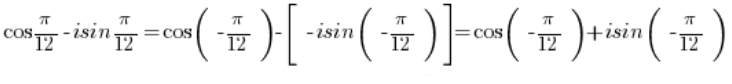
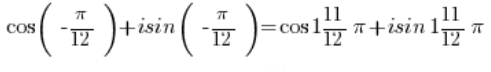
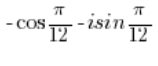ليس عدداً في الشكل المثلثي لأن أمام الوحدة التخيلية ‘i’ مضروبة في الجيب يوجد علامة ناقص، بينما يجب أن تكون زائد، وكذلك أمام الجيب التمام يوجد علامة ناقص، بينما يجب أن تكون زائد.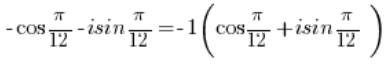
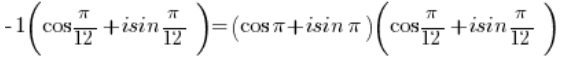
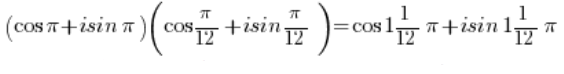
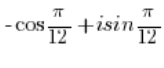إلى الشكل المثلثي (هذا ما نتقنه الآن…):
ليس عدداً مركباً في الشكل المثلثي لأن قبل الكوسينوس يوجد علامة ناقص، ويجب أن تكون زائد.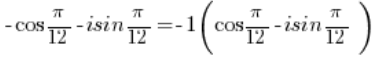
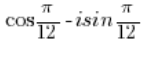إلى الشكل المثلثي (كما فعلنا في النقطة 2).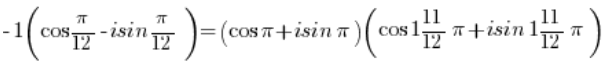
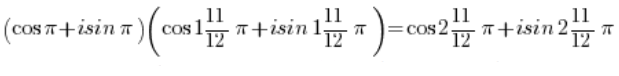
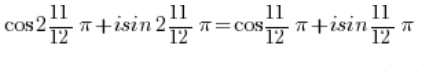
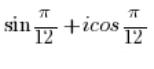ليس عدداً مركباً في الشكل المثلثي لأن قبل الكوسينوس توجد الوحدة التخيلية ‘i’ (ولا يجب أن تكون هناك)، وقبل الجيب لا توجد الوحدة التخيلية ‘i’.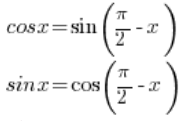
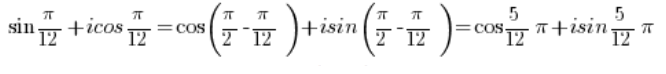
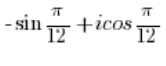ليس عدداً مركباً في الشكل المثلثي.
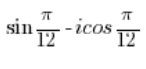ليس عدداً مركباً في الشكل المثلثي.
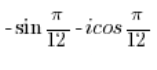ليس عدداً مركباً في الشكل المثلثي.حظاً موفقاً! 🙂
