Rząd macierzy Wykład 2
Temat: Sprawdzanie, czy wektory tworzą bazę w przestrzeni liniowej
Streszczenie
W artykule pokażę, jak użyć rząd macierzy do sprawdzenia, czy wektory tworzą bazę przestrzeni liniowej.
Kiedy wektory tworzą bazę w przestrzeni liniowej?
Kilka wektorów nazywamy bazą przestrzeni liniowej, kiedy spełnione są dwa warunki:
- Wektory te są liniowo niezależne (tu właśnie wykorzystuje się rząd macierzy)
- Każdy inny wektor z tej samej przestrzeni można przedstawić jako kombinację liniową tych wektorów
Czyli żeby sprawdzić, czy kilka wektorów tworzy bazę trzeba pokazać, że spełniają one te dwa warunki.
Obliczanie liniowej niezależności wektorów
Tutaj sprawa jest prosta. Wektory ustawiamy wierszami (albo kolumnami) w macierz. Liczymy rząd macierzy. Rząd macierzy to maksymalna liczba niezależnych wektorów ją tworzących. Jeżeli więc rząd macierzy wyjdzie równy liczbie wektorów ją tworzących, to są one liniowo niezależne. Jeżeli nie wyjdzie równy – są liniowo zależne (i nie tworzą bazy w danej przestrzeni).
Wykazywanie, że każdy wektor da się wyrazić jako kombinację liniową wektorów liniowo niezależnych
Tutaj bierzemy jakiś dowolny wektor z danej przestrzeni i pokazujemy, że istnieją (lub nie) takie stałe, które pomnożone przez wektory mające stanowić bazę i dodane do siebie będą równe temu dowolnemu wektorowi. Jak to się robi – pokażę dalej w przykładzie.
Przykład (zadanie)
Przykładowo możemy zrobić takie zadanie:
Zadanie 1
Sprawdź, czy wektory: 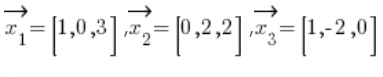 tworzą bazę w przestrzeni liniowej
tworzą bazę w przestrzeni liniowej ![]() , a jeśli tak, to przedstaw jako ich kombinację liniową wektor
, a jeśli tak, to przedstaw jako ich kombinację liniową wektor 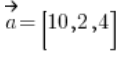 .
.
Zaczynamy od sprawdzenia liniowej niezależności tych wektorów. Układamy je w macierz i liczymy jej rząd:
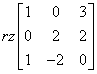 Liczymy, liczymy, liczymy (jak to dokładnie zrobić, jest pokazane na przykład w moim Kursie Macierzy) i mamy wynik:
Liczymy, liczymy, liczymy (jak to dokładnie zrobić, jest pokazane na przykład w moim Kursie Macierzy) i mamy wynik:
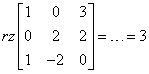 Jeśli rząd macierzy równy jest 3, a wektory też są trzy oznacza to, że są one liniowo niezależne. Pierwszy warunek tego, aby wektory tworzyły bazę w przestrzeni linowej
Jeśli rząd macierzy równy jest 3, a wektory też są trzy oznacza to, że są one liniowo niezależne. Pierwszy warunek tego, aby wektory tworzyły bazę w przestrzeni linowej ![]() jest spełniony.
jest spełniony.
W drugim warunku pokazać musimy, że dowolny wektor należący do przestrzeni ![]() (czyli trójwymiarowy) można przedstawić jako sumę wektorów tworzących – jakoby – bazę przemnożonych przez stałe. Można zapisać ten warunek jako:
(czyli trójwymiarowy) można przedstawić jako sumę wektorów tworzących – jakoby – bazę przemnożonych przez stałe. Można zapisać ten warunek jako:
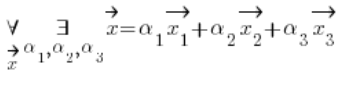
Przechodząc na zapis ze współrzędnymi wektorów i z ich postacią kolumnową (wygodniejszą) ten warunek wyglądać będzie tak:
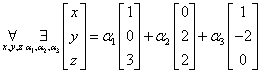 Po przemnożeniu przez stałe otrzymamy:
Po przemnożeniu przez stałe otrzymamy:
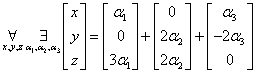 A po dodaniu do siebie macierzy po prawej:
A po dodaniu do siebie macierzy po prawej:
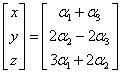 Powyższe równanie da nam układ równań:
Powyższe równanie da nam układ równań:
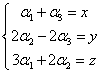 Zwróćmy uwagę, że ten układ ZAWSZE ma rozwiązanie, niezależnie od tego, ile są równe x,y,z bo wyznacznik główny układu (ze wzorów Cramera) jest różny od zera:
Zwróćmy uwagę, że ten układ ZAWSZE ma rozwiązanie, niezależnie od tego, ile są równe x,y,z bo wyznacznik główny układu (ze wzorów Cramera) jest różny od zera:
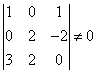 Zatem dla dowolnych x,y,z znajdą się takie
Zatem dla dowolnych x,y,z znajdą się takie ![]() , że układ będzie miał rozwiązanie. Zatem dowolny wektor z przestrzeni liniowej
, że układ będzie miał rozwiązanie. Zatem dowolny wektor z przestrzeni liniowej ![]() można przedstawić jako kombinację liniową wektorów
można przedstawić jako kombinację liniową wektorów ![]() .
.
Mamy więc odpowiedź. Wektory ![]() tworzą bazę w przestrzeni liniowej
tworzą bazę w przestrzeni liniowej ![]() .
.
Przypomnijmy sobie polecenie:
Sprawdź, czy wektory: 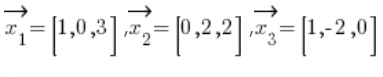 tworzą bazę w przestrzeni liniowej
tworzą bazę w przestrzeni liniowej ![]() , a jeśli tak, to przedstaw jako ich kombinację liniową wektor
, a jeśli tak, to przedstaw jako ich kombinację liniową wektor 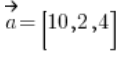 .
.
Czyli nasza misja nie jest skończona, trzeba jeszcze będzie wektor 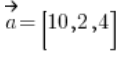 przedstawić jako kombinację liniową wektorów
przedstawić jako kombinację liniową wektorów 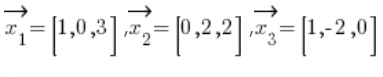 , czyli znaleźć takie stałe
, czyli znaleźć takie stałe ![]() , że:
, że:
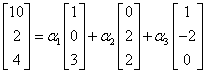 Po przemnożeniu przez stałe wektorów po prawej:
Po przemnożeniu przez stałe wektorów po prawej:
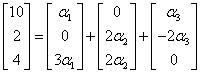 Po dodaniu wektorów po prawej:
Po dodaniu wektorów po prawej:
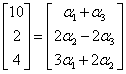 Co można zapisać jako układ równań:
Co można zapisać jako układ równań:
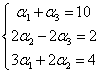 Ten układ rozwiązujemy – na przykład – wzorami Cramera i mamy wynik:
Ten układ rozwiązujemy – na przykład – wzorami Cramera i mamy wynik:
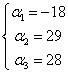 Zatem nasz wektor przedstawiony jako kombinację liniową trzech wektorów można zapisać tak:
Zatem nasz wektor przedstawiony jako kombinację liniową trzech wektorów można zapisać tak:
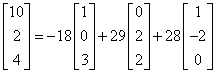 I to jest nasza odpowiedź.
I to jest nasza odpowiedź.
Zróbmy jeszcze przykład, w którym wektory NIE będą liniowo niezależne, co wykaże rząd macierzy.
Zadanie 2
Sprawdź, czy wektory: ![]() tworzą bazę w przestrzeni liniowej
tworzą bazę w przestrzeni liniowej ![]() .
.
Aby sprawdzić liniową niezależność wektorów liczymy rząd odpowiedniej macierzy:
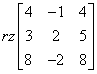 Liczymy, liczymy, liczymy i mamy wynik: 2. Zatem tylko 2 spośród tych 3 są liniowo niezależne. Czyli te 3 wektory jako całość nie są liniowo niezależne. Zatem nie tworzą bazy przestrzeni
Liczymy, liczymy, liczymy i mamy wynik: 2. Zatem tylko 2 spośród tych 3 są liniowo niezależne. Czyli te 3 wektory jako całość nie są liniowo niezależne. Zatem nie tworzą bazy przestrzeni ![]() . Sprawa zamknięta, piszemy odpowiedź.
. Sprawa zamknięta, piszemy odpowiedź.
Kliknij, aby przypomnieć sobie, czym jest rząd macierzy (poprzedni Wykład) <–

Kasia24
Co się dzieje, kiedy wyznacznik jest równy zero?
Krystian Karczyński
Wtedy wektory są liniowo zależne.
mtbchn
Nieaktualne, już policzone 🙂
mtbchn
[tex]
[/latex][/latex]A= \left[ \begin{matrix}{cccccc} -1 & 1 & 2 & 2 & 4 & 9\ 0 & 5 & 3 &-7 &-6 &-7\ 0 & 0 &-1 &-13 & 28 & 1\ 0 & 0 & 0 &-61 & 130 & 8\ 0 & 0 & 0 & 28 &-69 &-13 \end{matrix} \right] q\quad[/tex]mtbchn
Dzień dobry,Mam problem z układem równań, który liczę metodą Gaussa. Dochodzę do poniższego etapu i nie jestem w stanie dalej ruszyć. Mogę prosić o pomoc, jak doprowadzić macierz schodkową do końca? Z góry dziękuję. -1 1 2 2 4 90 5 3 -7 -6 -70 0 -1 -13 28 10 0 0 -61 130 80 0 0 28 -69 -13
mtbchn
[/latex][/latex]A= \left[ \begin{matrix}{cccccc} -1 & 1 & 2 & 2 & 4 & 9\ 0 & 5 & 3 &-7 &-6 &-7\ 0 & 0 &-1 &-13 & 28 & 1\ 0 & 0 & 0 &-61 & 130 & 8\ 0 & 0 & 0 & 28 &-69 &-13 \end{matrix} \right] q\quadMagdalena
Witam, proszę o rozwiązanie tego zadania:Macierz przejścia od bazy v’ do bazy v ma postać (1 1, 2 1). Wektor x=[3,1]v’ ma w bazie v współrzędne:A. [4,7] B.[-2,2] C[2,-5] D. Wymienione odpowiedzi są błędne
baza
Wytłumaczone nieźle. Zastanawiam się tylko, po co znajdować bazę w ten sposób. Jak już udowodniliśmy liniową niezależność wektorów (zadanie 1) i dim(R3)=3, a wektory są 3, to to już jest koniec. Z definicji baza jest maksymalnym układem wektorów liniowo niezależnych danej przestrzeni liniowej. Skoro w przestrzeni trójwymiarowej znaleźliśmy trzy wektory liniowo niezależne, to wiadomo, że jest to maksymalny układ wektorów liniowo niezależnych, więc jest bazą podanej przestrzeni.
Karolina
Mogę prosić o szybką pomoc?
1.Udowodnij, że podany zbiór jest przestrzenią liniową oraz określ wymiar i znajdź jej bazę:
a){(x,y,z) należy do R^3 x+y+z=0}
b){(x,y,z,t) należy do R^4 2x-3t=0, 3y+z=t, x-y=z}
agata123
Czy można sprawdzić czy wektory twarzą baze przestrzeni tworzac wyznacznik z wektorów, kolejne wektory zapisywać jako kolomnu macierzy, poziczyc wyznacznik, i jeśli det jesr rózny od zero to znaczy ze wektory tworzą baze?
Krystian Karczyński
Tak.
Tomasz
Panie Krystianie, znalazłem błąd rachunkowy. Wynikiem Y (alfa 2) nie jest 29, a 26, ponieważ wyznacznik macierzy Wy jest równy -52 a nie -58.
Pozdrawiam
Maciej
Witam, mam pytanie, w przypadku, gdy mamy taki przypadek
x=(1,0,1) y=(1,2,2) i mamy sprawdzić czy układ jest bazą R^3 // z założenia raczej wychodzi, że baza jest trójwymiarowa, a my mamy tylko 2 wektory, więc na wstępie już widać, że są liniowo zależne i nie mogą być bazą.
Ale, jak należałoby teraz postępować, aby dobrać wektor z, który spełniałby warunek liniowej niezależności ?
Marek
Hej, Witam
Bardzo dobry i jasny wykład.Myślę ze dobrym pomysłem było by napisanie takiego dobrego E booka z wykładami. Był by doskonałym uzupełnieniem istniejących kursów.
No i E-booki nie są ograniczone ilością stron.
Marek
mstr
W pierwszym przykładzie, pisze Pan:
„Zwróćmy uwagę, że ten układ ZAWSZE ma rozwiązanie, niezależnie od tego, ile są równe x,y,z bo wyznacznik główny układu (ze wzorów Cramera) jest różny od zera:”
Układ jest ten: https://blog.etrapez.pl/wp-content/uploads/sites/3/2010/08/Eqn48.gif
1 1 1
2 -2 1
3 2 1
tak wg mnie powinien wygladać wyznacznik, a Pan liczy wyznacznik dla https://blog.etrapez.pl/wp-content/uploads/sites/3/2010/08/Eqn49.gif
Czy to błąd czy ja czegoś nie rozumiem?
Krystian Karczyński
Jeżeli jakiejś zmiennej (na przykład {{\alpha }_{2}}w pierwszym równaniu) nie ma w ogóle w równaniu, przyjmujemy, że współczynnik liczbowy przy niej równy jest zero, dlatego jeśli równanie jest: {{\alpha }_{1}}+{{\alpha }_{3}}=xto pierwszy wiersz w wyznaczniku głównym tego równania będzie równy 1 0 1 (bo nie ma w nim {{\alpha }_{2}}).
annafrompoland
Witam panie Krystianie, proszę mnie naprowadzić – nasz wykładowca mówi, że aby stwierdzić że wektory tworzą bazę wystarczy udowodnić JEDEN z tych warunków, czyli pokazać że są liniowo niezależne ALBO generują przestrzeń, Pan pisze natomiast że muszą spełniać oba a to istotna różnica. W \internecie można napotkać obie te opinie, nam wyraźnie powiedziano że wystarczy udowodnić np liniową niezależność. Proszę o odpowiedź.
ignacy
To co twój wykładowca mówił zachodzi, gdy liczba wektorów jest równa wymiarowi przestrzeni. W przeciwnym wypadku trzeba sprawdzić oba warunki.
Definicja 4.8 i Twierdzenie 4.16)