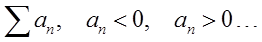
Szereg o Wyrazach Niedodatnich? – Żaden Problem z Kryteriami Abela i Dirichleta

---

Wprowadzenie

W ostatnim poście na blogu pokazałem kilka dodatkowych kryteriów, których użyć można do określenia zbieżności szeregów o wyrazach dodatnich.

Czas więc na lekkie wzmocnienie artylerii na odcinku szeregów o wyrazach już niekoniecznie dodatnich. Dużym problemem studentów jest to, że mechanicznie próbują stosować kryterium d’Alemberta, porównawcze, całkowe itd. w przypadkach, w których tych kryteriów stosować nie można już na starcie.

Dotyczą one bowiem szeregów \sum\limits_{n=1}^{\infty }{{{a}_{n}}}, w których {{a}_{n}}\ge 0. To, że jest to 90% przykładów na studiach to inna sprawa, bo na kolokwium przecież Pan Profesor może rzucić “podkręconą” piłkę i ustawienie rakiety działające w 90% wyuczonych przypadków zakończy się katastrofą już na starcie.

Co począć z tymi szeregami \sum\limits_{n=1}^{\infty }{{{a}_{n}}}, które mają wyrazy {{a}_{n}} ujemne?

Zbieżność bezwzględna i kryterium Leibnitz’a

Jeśli uczyłeś się już z mojego Kursu Szeregów, to już wiesz, jak radzić sobie wtedy z:

1. Szeregami zbieżnymi bezwzględnie (wykazać zbieżność szeregu \sum\limits_{n=1}^{\infty }{\left| {{a}_{n}} \right|} i po sprawie)
2. Szeregami naprzemiennymi \sum\limits_{n=1}^{\infty }{{{\left( -1 \right)}^{n}}{{a}_{n}}}\quad {{a}_{n}}\ge 0 aha, no i jeszcze oczywiście:
3. Szeregami, które nie spełniają warunku koniecznego zbieżności \underset{n\to \infty }{\mathop{\lim }}\,{{a}_{n}}=0

A co zresztą? Czyli szeregami o wyrazach dowolnych rozbieżnymi bezwzględnie, nie-naprzemiennymi i spełniającymi warunek zbieżności?

Zajmę się nimi w tym poście – wprowadzając dwa nowe kryteria, nie wymagające założenia o nieujemności wyrazów szeregu.

Kryteria Abela i Dirichleta

Kryterium Abela

Jeżeli mamy szereg, którego wyraz ogólny możemy zapisać jako iloczyn wyrazów dwóch ciągów, tzn. \sum\limits_{n=1}^{\infty }{{{a}_{n}}{{b}_{n}}}, wtedy:

• jeżeli szereg \sum\limits_{n=1}^{\infty }{{{b}_{n}}} jest zbieżny, a ciąg {{a}_{n}} monotoniczny i ograniczony, to szereg \sum\limits_{n=1}^{\infty }{{{a}_{n}}{{b}_{n}}} jest zbieżny

W praktyce więc wyjściowy wyraz szeregu staram się rozbić na dwa takie ciągi, żeby szereg z jednego był zbieżny, a drugi był monotoniczny (czyli albo rosnący, albo stały, albo malejący) i ograniczony (jakąś liczbą).

Kryterium Dirichleta

Jeżeli mamy szereg, którego wyraz ogólny możemy zapisać jako iloczyn wyrazów dwóch ciągów, tzn. \sum\limits_{n=1}^{\infty }{{{a}_{n}}{{b}_{n}}}, wtedy:

• jeżeli sumy częściowe szeregu \sum\limits_{n=1}^{\infty }{{{b}_{n}}} są wspólnie ograniczone (tzn. ograniczone jedną stałą z góry i jedną z dołu), a ciąg {{a}_{n}} monotoniczny i zbieżny do zera, to szereg \sum\limits_{n=1}^{\infty }{{{a}_{n}}{{b}_{n}}} jest zbieżny

 

Wyjściowy wyraz szeregu więc staramy się rozbić na dwa ciągi ( {{a}_{n}} i {{b}_{n}}) takie, że sumy częściowe z jednego szeregu są ograniczone, a drugi jest monotoniczny i zbiega do zera.

Przykład 1

Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\frac{\sin n}{n}}.

Tego “na oko” prostego do zbadania szeregu nie możemy nawet próbować porównawczym ( \sin n może przyjmować wartości a to dodatnie, a to ujemne i wcale nie na przemian).

Zbieżność bezwzględna szeregu również wysiada, szereg nie jest naprzemienny, więc na nic Leibnit’z.

Jest to natomiast bardzo typowe zadanie na kryterium Abela i Dirichleta. Na początku w tego typu zadaniach musisz wyprowadzić sobie dwie tożsamości (nie związane bezpośrednio z tymi kryteriami). Pomogą Ci one w szacowaniach ograniczenia stałą w kryterium Dirichleta.

Oto one:

Pomocne tożsamości trygonometryczne

\sum\limits_{k=1}^{n}{\sin kx}=\frac{\cos \tfrac{1}{2}x-\cos \left( n+\tfrac{1}{2} \right)x}{2\sin \tfrac{1}{2}x} \sum\limits_{k=1}^{n}{\cos kx}=\frac{\sin \left( n+\tfrac{1}{2} \right)x-\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}

Ja rozumiem, że zapamiętywanie takich rzeczy bardzo boli, ale tutaj po prostu nie da się inaczej. x w tych wzorach to może być dowolna liczba, np. dla x=1 miałbym:

\sum\limits_{k=1}^{n}{\sin k}=\frac{\cos \tfrac{1}{2}-\cos \left( n+\tfrac{1}{2} \right)}{2\sin \tfrac{1}{2}}

Teraz Ci pokażę, skąd się wzięły te wzory:

\sum\limits_{k=1}^{n}{\sin kx}=\sin x+\sin 2x+\sin 3x+\ldots +\sin nx=\frac{2\sin x\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}+\frac{2\sin 2x\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}+\frac{2\sin 3x\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}+\ldots +\frac{2\sin nx\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}=\frac{1}{2\sin \tfrac{1}{2}x}\left( 2\sin x\sin \tfrac{1}{2}x+2\sin 2x\sin \tfrac{1}{2}x+2\sin 3x\sin \tfrac{1}{2}x+\ldots +2\sin nx\sin \tfrac{1}{2}x \right)

W szkole średniej (poziom rozszerzony) było takie cudo, jak wzór na różnicę cosinusów (za moich czasów trzeba było to kuć na pamięć, teraz wystarczą tablice):

\cos \alpha -\cos \beta =-2\sin \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2}

Spójrz, jak przy jego pomocy iloczyny sinusów w nawiasie możesz przedstawić jako różnicę cosinusów (stosując ten wzór jakby “w drugą stronę”):

Jeśli się zauważy, że \alpha =1\frac{1}{2}x,\beta =\frac{1}{2}x, widać, że można zapisać:

2\sin x\sin \tfrac{1}{2}x=-\left( -2\sin \frac{1\tfrac{1}{2}x+\tfrac{1}{2}x}{2}\sin \frac{1\tfrac{1}{2}x-\tfrac{1}{2}x}{2} \right)=-\left( \cos 1\tfrac{1}{2}x-\cos \tfrac{1}{2}x \right)=\cos \tfrac{1}{2}x-\cos 1\tfrac{1}{2}x

Jeśli się zauważy, że \alpha =2\frac{1}{2}x,\beta =1\frac{1}{2}x, widać, że można zapisać:

2\sin 2x\sin \tfrac{1}{2}x=-\left( -2\sin \frac{2\tfrac{1}{2}x+1\tfrac{1}{2}x}{2}\sin \frac{2\tfrac{1}{2}x-1\tfrac{1}{2}x}{2} \right)=-\left( \cos 2\tfrac{1}{2}x-\cos 1\tfrac{1}{2}x \right)=\cos 1\tfrac{1}{2}x-\cos 2\tfrac{1}{2}x

Jeśli się zauważy, że \alpha =3\frac{1}{2}x,\beta =2\frac{1}{2}x, widać, że można zapisać:

2\sin 3x\sin \tfrac{1}{2}x=-\left( -2\sin \frac{3\tfrac{1}{2}x+2\tfrac{1}{2}x}{2}\sin \frac{3\tfrac{1}{2}x-2\tfrac{1}{2}x}{2} \right)=-\left( \cos 3\tfrac{1}{2}x-\cos 2\tfrac{1}{2}x \right)=\cos 2\tfrac{1}{2}x-\cos 3\tfrac{1}{2}x

…

Jeśli się zauważy, że \alpha =\left( n+\frac{1}{2} \right)x,\beta =\left( n-\frac{1}{2} \right)x, widać, że można zapisać:

2\sin nx\sin \tfrac{1}{2}x=-\left( -2\sin \frac{\left( n+\tfrac{1}{2} \right)x+\left( n-\tfrac{1}{2} \right)x}{2}\sin \frac{\left( n+\tfrac{1}{2} \right)x-\left( n-\tfrac{1}{2} \right)x}{2} \right)=-\left( \cos \left( n+\tfrac{1}{2} \right)x-\left( n-\tfrac{1}{2} \right)x \right)=\cos \left( n-\tfrac{1}{2} \right)x-\cos \left( n+\tfrac{1}{2} \right)x

Czyli wracając do naszego wyprowadzenia:

\sum\limits_{k=1}^{n}{\sin kx}=\sin x+\sin 2x+\sin 3x+\ldots +\sin nx=\frac{2\sin x\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}+\frac{2\sin 2x\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}+\frac{2\sin 3x\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}+\ldots +\frac{2\sin nx\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}=\frac{1}{2\sin \tfrac{1}{2}x}\left( 2\sin x\sin \tfrac{1}{2}x+2\sin 2x\sin \tfrac{1}{2}x+2\sin 3x\sin \tfrac{1}{2}x+\ldots +2\sin nx\sin \tfrac{1}{2}x \right) =\frac{1}{2\sin \tfrac{1}{2}x}\left( \left( \cos \tfrac{1}{2}x-\cos 1\tfrac{1}{2}x \right)+\left( \cos 1\tfrac{1}{2}x-\cos 2\tfrac{1}{2}x \right)+\left( \cos 2\tfrac{1}{2}x-\cos 3\tfrac{1}{2}x \right)+\ldots +\left( \cos \left( n-\tfrac{1}{2} \right)x-\cos \left( n+\tfrac{1}{2} \right)x \right) \right)=

Tutaj widać elegancko, że każdy “drugi” składnik w “wewnętrznych” nawias “skraca się” z pierwszym z następnego, zostanie mi więc tylko:

=\frac{1}{2\sin \tfrac{1}{2}x}\left( \cos \tfrac{1}{2}x-\cos \left( n+\tfrac{1}{2} \right)x \right)=\frac{\cos \tfrac{1}{2}x-\cos \left( n+\tfrac{1}{2} \right)x}{2\sin \tfrac{1}{2}x}

Pokazałem więc w ten sposób, co miałem pokazać, tzn. że:

\sum\limits_{k=1}^{n}{\sin kx}=\frac{\cos \tfrac{1}{2}x-\cos \left( n+\tfrac{1}{2} \right)x}{2\sin \tfrac{1}{2}x}

Trochę się przy tym zasapałem, wykazanie więc wzoru:

\sum\limits_{k=1}^{n}{\cos kx}=\frac{\sin \left( n+\tfrac{1}{2} \right)x-\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x} zostawiam Tobie. Zrobisz to analogicznie, tyle, że musisz “podejść” do wzoru na różnicę sinusów: \sin \alpha -\sin \beta =2\cos \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2}(w razie kłopotów daj znać w komentarzach pod postem).

 Zastosowanie kryterium Dirichleta do przykładu 1

Wracajmy więc do gry, tzn. do wykazania zbieżności szeregu \sum\limits_{n=1}^{\infty }{\frac{\sin n}{n}}. Wyraz szeregu rozbijam na mnożenie dwóch ciągów (tak, żeby pasowało mi to do Dirichleta):

\sum\limits_{n=1}^{\infty }{\frac{\sin n}{n}}=\sum\limits_{n=1}^{\infty }{\frac{1}{n}\cdot \sin n}

Podchodzę teraz do kryterium Dirichleta – szereg jednego z tych ciągów ma mieć wspólnie ograniczone sumy cząstkowe, a drugi ciąg ma być monotoniczny dążący do zera.

Pokażę, że ograniczone sumy cząstkowe ma szereg \sum\limits_{n=1}^{\infty }{\sin n}, a ciąg \frac{1}{n} jest ograniczony i zbieżny do zera.

Wykazanie ograniczenia sum cząstkowych

Weźmy sumy cząstkowe szeregu \sum\limits_{n=1}^{\infty }{\sin n}(pokazuję jak je budować w moim Kursie Szeregów na Lekcji 1, przy okazji badania sumy z definicji):

{{S}_{1}}=\sin 1 {{S}_{2}}=\sin 1+\sin 2 {{S}_{3}}=\sin 1+\sin 2+\sin 3 \ldots {{S}_{n}}=\sin 1+\sin 2+\sin 3+\ldots +\sin n=\sum\limits_{k=1}^{n}{\sin k}

Czy wyraz ogólny sum cząstkowych coś Ci przypomina? Oczywiście, troszkę wyżej mozolnie wyprowadzałem wzór:

\sum\limits_{k=1}^{n}{\sin kx}=\frac{\cos \tfrac{1}{2}x-\cos \left( n+\tfrac{1}{2} \right)x}{2\sin \tfrac{1}{2}x}

Skoro tak, to znaczy, że (przyjmując w tym ogólnym wzorze x=1):

{{S}_{n}}=\sin 1+\sin 2+\sin 3+\ldots +\sin n=\sum\limits_{k=1}^{n}{\sin k}=\frac{\cos \tfrac{1}{2}-\cos \left( n+\tfrac{1}{2} \right)}{2\sin \tfrac{1}{2}}

Zauważ, że wyrażenie w liczniku: \cos \tfrac{1}{2}-\cos \left( n+\tfrac{1}{2} \right) będzie przyjmować różne wartości (w zależności od n), ale na pewno nie przekroczy -2 i 2 (bo wartości cosinusów “wahają się” pomiędzy -1 i 1).

Zatem można stwierdzić, że:

\frac{-2}{2\sin \tfrac{1}{2}}\le \frac{\cos \tfrac{1}{2}-\cos \left( n+\tfrac{1}{2} \right)}{2\sin \tfrac{1}{2}}\le \frac{2}{2\sin \tfrac{1}{2}}

Czyli:

-\frac{1}{\sin \tfrac{1}{2}}\le {{S}_{n}}\le \frac{1}{\sin \tfrac{1}{2}}

Zatem pokazałem, że wszystkie wyrazy ciągu sum częściowych są ograniczone od dołu i od góry stałymi ( -\frac{1}{\sin \tfrac{1}{2}} i \frac{1}{\sin \tfrac{1}{2}}).

Wykazanie monotoniczności i zbieżności ciągu

Ciąg \frac{1}{n}=1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\ldots i jest to oczywiście ciąg malejący (czyli monotoniczny). Wykazywanie tego to już chyba trochę przesada, ale oczywiście można np. z definicji ciągu malejącego ze szkoły średniej.

Oczywiście też, że: \underset{n\to \infty }{\mathop{\lim }}\,\frac{1}{n}=0.

Czyli warunki z kryterium Dirichleta mam spełnione.

Zatem:

Na mocy kryterium Dirichleta szereg \sum\limits_{n=1}^{\infty }{\frac{\sin n}{n}} jest zbieżny.

Uogólnienie przykładu 1

Mając pod ręką tożsamości:

\sum\limits_{k=1}^{n}{\sin kx}=\frac{\cos \tfrac{1}{2}x-\cos \left( n+\tfrac{1}{2} \right)x}{2\sin \tfrac{1}{2}x} \sum\limits_{k=1}^{n}{\cos kx}=\frac{\sin \left( n+\tfrac{1}{2} \right)x-\sin \tfrac{1}{2}x}{2\sin \tfrac{1}{2}x}

i kryterium Dirichleta dosyć łatwo da się wykazać zbieżność każdego szeregu postaci:

\sum\limits_{n=1}^{\infty }{{{a}_{n}}\sin nx} lub \sum\limits_{n=1}^{\infty }{{{a}_{n}}\cos nx}

gdzie {{a}_{n}} może oznaczać dowolny, byle jaki ciąg (byle spełniał warunki kryterium Dirichleta…). Po prostu korzystając z tożsamości pokazujemy ograniczoność sum częściowych szeregów \sum\limits_{k=1}^{n}{{{a}_{n}}\sin nx} lub \sum\limits_{k=1}^{n}{{{a}_{n}}\cos nx}(tak jak pokazałem to wyżej) i przed nami już tylko wykazanie, że ciąg {{a}_{n}} jest monotoniczny i zbieżny do zera (niestety, nie zawsze jest to takie proste jak wyżej).

A tak się składa, że przykłady typu \sum\limits_{n=1}^{\infty }{{{a}_{n}}\sin nx}, \sum\limits_{n=1}^{\infty }{{{a}_{n}}\cos nx} to ulubione, podręcznikowe przykłady profesorów na zajęciach.