Wzory Na Prawdopodobieństwo – Wszystkie W Jednym Miejscu

---

Wzory na prawdopodobieństwo

W tym pliku PDF znajdziesz wszystkie potrzebne Ci  na studiach wzory do prawdopodobieństwa, gotowe do wydrukowania:

Wzory na prawdopodobieństwo (PDF)

Tablice rozkładu normalnego (PDF)

Dalej poście chciałbym zająć się wyprowadzeniem podstawowych własności i wzorów na prawdopodobieństwo:

Własności prawdopodobieństwa

1. P(A) \in <0,1>
2. P(\varnothing)=0
3. A \subseteq B \Rightarrow P\left(A\right)\le P\left(B\right)
4. P\left( A' \right)=1-P\left( A \right)
5. A \subseteq B \Rightarrow P\left(B \backslash A \right)=P\left( B \right)-P\left( A \right)
6. P\left( A \cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A \cap B \right)

Te własności i wzory wynikają z definicji (zerknij na nią koniecznie, zanim ruszysz dalej), ale nie są w niej podane bezpośrednio. Profesorzy na egzaminach z teorii lubią zadawać zadania na “wyprowadzenie” ich.

Własności prawdopodobieństwa

I. P(A) \in <0,1>

Faktycznie, w definicji prawdopodobieństwa nigdzie nie jest napisane, że musi ono przyjmować wartości mniejsze od 1. Może więc jakoś może przyjąć wartość np. 7 ?

Ano nie może. Jest to jednak dopiero wniosek z definicji. A tutaj krok po kroku, dlaczego nie może:

1. Należy pokazać, że wartości funkcji są większe lub równe od zera i jednocześnie mniejsze lub równe od jeden, czyli:

P\left( A \right)\ge 0 i P\left( A \right)\le 1

2. To, że P\left( A \right)\ge 0 wynika od razu z Aksjomatu 1.
3. Trzeba tylko wykazać, że z aksjomatów wynika, że P\left( A \right)\le 1.

Wiemy, że:

\Omega =A\cup {A}'

…czyli, że cały zbiór zdarzeń elementarnych to suma dowolnego zbioru A i jego dopełnienia. Czyli każde zdarzenie elementarne albo należy do A, albo nie należy do A (czyli należy do dopełniania A). Zatem:

P(Ω) =P\left( A\cup {A}' \right)

4. Z Aksjomatu 2 wiem, że P(Ω)=1. Zdarzenia A i A’ są rozłączne (nie mają wspólnych elementów), czyli z Aksjomatu 3 wiem, że P\left( A\cup {A}' \right)=P\left( A \right)+P\left( {{A}'} \right).

Mogę zapisać więc:

1=P\left( A \right)+P\left( {{A}'} \right)
5. Przekształcając mam:

P\left( A \right)=1-P\left( {{A}'} \right)

A z tego wniosek, że P\left( A \right) jest zawsze mniejsze lub równe od 1, bo P\left( {{A}'} \right) jest zawsze większe lub równe od 0 (z Aksjomatu 1, który oczywiście dotyczy prawdopodobieństwa każdego zdarzenia, niezależnie od użytej tam literki).

6. Czyli pokazałem, że prawdopodobieństwo dowolnego zdarzenia A nie może być większe od 1 🙂

 II.  P(\varnothing)=0

W definicji nigdzie nie jest wprost napisane, że prawdopodobieństwo zdarzenia niemożliwego musi być równe zero. Ale można pokazać, że to z niej wynika:

1. Jeśli do dowolnego zbioru dodamy zbiór pusty otrzymamy ten sam zbiór. Także do zbioru wszystkich zdarzeń Ω. Zatem: \Omega =\Omega \cup \varnothing Czyli:P(Ω)=P(ΩυØ)
2. Zdarzenia Ω i Ø są rozłączne (nie mają wspólnych elementów), zatem zgodnie z Aksjomatem 3definicji mogę napisać, że:P(Ω)=P(ΩυØ)=P(Ω)+P(Ø)czyli:P(Ω)=P(Ω)+P(Ø)
3. Zgodnie z Aksjomatem 2P(Ω)=1, zatem mam:1 = 1 + P(Ø)
   P(Ø)=0

i nie może być inaczej 🙂

III. A \subseteq B \Rightarrow P\left(A\right)\le P\left(B\right)

Tutaj zakładam, że A \subseteq B, czyli mam do czynienia z czymś takim:

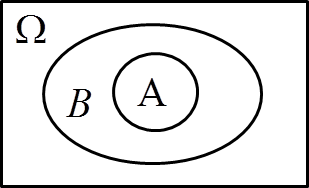
1. Teraz zauważam, że zbiór B mogę podzielić na dwa zbiory: zbiór A i to, co jest w B ale nie jest w A, czyli zbiór  B \ A:

czyli:

B = A \cup (B\A)

czyli:

P(B)=P(A \cup (B\A))

2. Zbiory A i B\\A są rozłączne, zatem zgodnie z Aksjomatem 3:

P(B)=P(A \cup (B\A))=P(A)+P(B\A)

czyli:

P(A)=P(B)-P(B\A)

3. Stąd wniosek, że P\left( A \right)\le P\left( B \right), bo P\left( B \backslash A \right)\ge 0– zgodnie z Aksjomatem 1 (który dotyczy każdego prawdopodobieństwa, niezależnie od literki).

IV. P\left( A' \right)=1-P\left( A \right)

Działam podobnie, jak wykazując własność I.

1. Wiem, że cały zbiór zdarzeń elementarnych \Omega można podzielić na sumę jakiegoś dowolnego zbioru A i jego dopełnienia A':

\Omega =A\cup {A}'

czyli:

P(Ω) =P\left( A\cup {A}' \right)

2. Korzystam z Aksjomatu 2, aby określić, że P(Ω)=1 i z Aksjomatu 3, bo zdarzenia  A i A' są rozłączne. Mam więc:

1=P\left( A \right)+P\left( {{A}'} \right)

czyli:

P\left( A \right)=1-P\left( {{A}'} \right)

co właśnie miałem pokazać.

V. A \subseteq B \Rightarrow P\left(B \backslash A \right)=P\left( B \right)-P\left( A \right)

Działając analogicznie jak przy wykazywaniu własności III dochodzą do momentu, gdzie mam wzór:

P(B)=P(A \cup (B\\A))=P(A)+P(B\\A)

czyli:

P(B)=P(A)+P(B\\A)

stąd:

P(B\\A)=P(B)-P(A)

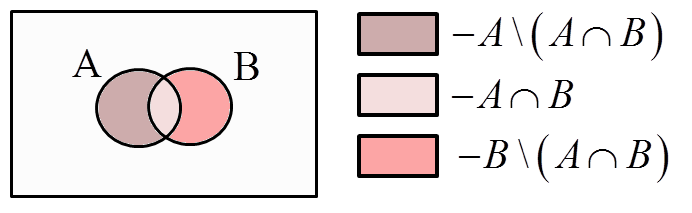
VI. P\left( A \cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A \cap B \right)

1. Sumę dwóch zbiorów A i B mogę podzielić na trzy zbiory:

A\backslash \left( A\cap B \right)– czyli wszystko, co należy do  A i nie należy do ich części wspólnej A\cap B

A\cap B– czyli część wspólną A i B

B\backslash \left( A\cap B \right) – czyli wszystko, co należy do  B i nie należy do ich części wspólnej A\cap B

Mam więc:

A\cup B=\left( A\backslash \left( A\cap B \right) \right)\cup \left( A\cap B \right)\cup \left( B\backslash \left( A\cap B \right) \right)

czyli:

P\left( A\cup B \right)=P\left( \left( A\backslash \left( A\cap B \right) \right)\cup \left( A\cap B \right)\cup \left( B\backslash \left( A\cap B \right) \right) \right)

2. Zdarzenia A\backslash \left( A\cap B \right), \left( A\cap B \right) i \left( B\backslash \left( A\cap B \right) \right) są rozłączne, zatem zgodnie z Aksjomatem 3 mogę zapisać, że:

P\left( A\cup B \right)=P\left( A\backslash \left( A\cap B \right) \right)+P\left( A\cap B \right)+P\left( B\backslash \left( A\cap B \right) \right)

3. Zdarzenie A\cap B zawiera się w zdarzeniu A, jak i w zdarzeniu B. Zgodnie z udowodnionym już wyżej wzorem (własnością) numer V mogę zapisać:

P\left( A\cup B \right)=P\left( A \right)-P\left( A\cap B \right)+P\left( A\cap B \right)+P\left( B \right)-P\left( A\cap B \right)

4. Porządkując, wychodzę na wzór:

P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)

który właśnie miałem udowodnić.

To już wszystko, jak widać ze stosunkowo “skromnej” w założenia definicji można wyprowadzić wiele ciekawych wzorów i własności.

Napisz mi proszę w komentarzach o swoich pytaniach i wątpliwościach związanych z prawdopodobieństwem i wzorami na nie 🙂

Kliknij tutaj, aby powrócić na główną stronę z materiałami o prawdopodobieństwie