Formulas For Probability – All In One Place

---

Probability Formulas

In this PDF you will find everything you need  in college probability formulas, ready to print:

Probability Formulas (PDF)

Normal distribution tables (PDF)

Further in the post I would like to deal with the derivation of the basic properties and formulas for probability:

Probability properties

1. P(A)\in< 0.1>
2. P(\varnothing)=0
3. A \subseteq B \Rightarrow P\left(A\right)\le P\left(B\right)
4. P\left( A' \right)=1-P\left( A\right)
5. A \subseteq B \Rightarrow P\left(B \backslash A \right)=P\left( B \right)-P\left( A \right)
6. P\left( A \cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A \cap B \right)

These properties and formulas follow from the definition (be sure to take a look at it before proceeding), but are not stated directly in it. Professors in theory exams like to give tasks to “derive” them.

Probability properties

I. P(A) \in< 0.1>

In fact, in The definition of probability nowhere says that it must take values ​​less than 1. So maybe it can somehow take a value of, for example, 7?

No, it can’t. However, this is only a conclusion from the definition. And here’s a step-by-step answer why it can’t:

1. It should be shown that the function values ​​are greater than or equal to zero and at the same time less than or equal to one, that is:

P\left( A \right)\ge 0 and P\left( A \right)\le 1

2. That P\left( A \right)\ge 0 follows immediately from Axiom 1 .
3. It only needs to be shown that the axioms imply that P\left( A \right)\le 1 .

We know that:

\Omega =A\cup{A} '

…that is, the entire set of elementary events is the sum of any set A and its complement. That is, every elementary event either belongs to A or does not belong to A (i.e. belongs to the complement of A). Therefore:

P(Ω) =P\left( A \cup{A}' \right)

4. From Axiom 2 I know that P(Ω)=1. The events A and A’ are disjoint (they have no elements in common), so from Axiom 3 I know that P\left( A\cup{A}' \right)=P\left( A \right)+P\left( {{A}'} \right) .

So I can write:

1=P\left( A \right)+P\left( {{A} '} \right)
5. After transforming I get:

P\left( A \right)=1-P\left( {{A} '} \right)

Hence, P\left( A \right) is always less than or equal to 1, because P\left( {A}' \right) is always greater than or equal to 0 (from Axiom 1 , which of course applies to the probability of any event, regardless of the letter used there).

6. So I showed that the probability of any event A cannot be greater than 1 🙂

 II.  P(\varnothing)=0

Nowhere in the definition does it explicitly say that the probability of an impossible event must be equal to zero. But it can be shown that it follows from this:

1. If we add the empty set to any set, we will get the same set. Also for the set of all Ω events. So: \Omega =\Omega \cup \varnothing
   So: P(Ω)=P(ΩυØ)
2. The events Ω and Ø are disjoint (they have no elements in common), so according to Axiom 3 of the definition I can write:
   P(Ω)=P(ΩυØ)=P(Ω)+P(Ø)
   that is:
   P(Ω)= P(Ω)+P(Ø)
3. According to Axiom 2 P(Ω)=1, so I have:
   1 = 1 + P(Ø)
   P(Ø)=0

and it can’t be otherwise 🙂

III. A \subseteq B \Rightarrow P\left(A\right)\le P\left(B\right)

Here I’m assuming A \subseteq B , so I’m dealing with something like this:

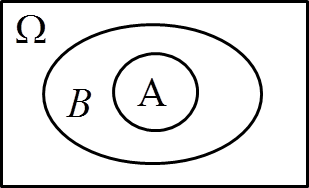
1. Now I notice that I can divide the set B into two sets: the set A and what is in B but not in A, i.e. the set  B \ A:

That is:

B = A \cup (B\A)

That is:

P(B)=P(A \cup (B\A))

2. Sets A and B\A are disjoint , so according to Axiom 3 :

P(B)=P(A \cup (B\A))=P(A)+P(B\A)

That is:

P(A)=P(B)-P(B\A)

3. Hence the conclusion that P\left( A \right)\le P\left( B \right) , because P\left( B \backslash A \right)\ge 0 – according to Axiom 1 (which applies to every probability regardless of the variable’s letter).

IV. P\left( A' \right)=1-P\left( A\right)

I act similarly to showing property I.

1. I know that the whole set of elementary events \Omega can be divided into the sum of some arbitrary set A and its complement A' :

\Omega =A\cup{A} '

That is:

P(Ω) =P\left( A\cup{A}'\right)

2. I use Axiom 2 to determine that P(Ω)=1 and Axiom 3, because the events  A and A' are disjoint. So I have:

1=P\left( A \right)+P\left( {{A} '} \right)

That is:

P\left( A \right)=1-P\left( {{A} '} \right)

what I was suppose to show.

V. A \subseteq B \Rightarrow P\left(B \backslash A \right)=P\left( B \right)-P\left( A \right)

Acting in the same way as when demonstrating property III, they reach the point where I have the formula:

P(B)=P(A \cup (B\A))=P(A)+P(B\A)

That is:

P(B)=P(A)+P(B\A)

hence:

P(B\A)=P(B)-P(A)

VI. P\left( A \cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A \cap B \right)

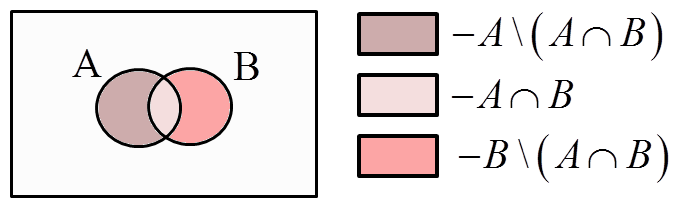
1. The union of two sets A and B can be divided into three sets:

A\backslash \left( A\cap B \right) – everything that belongs to  A and does not belong to their common part A\cap B

A\cap B – that is the common part of A and B

B\backslash \left( A\cap B \right)  – that is, everything that belongs to  B and does not belong to their common part A\cap B

So I have:

A\cup B=\left( A\backslash \left( A\cap B \right) \right)\cup \left( A\cap B \right)\cup \left( B\backslash \left( A\cap B \right) \right)

That is:

P\left( A\cup B \right)=P\left( \left( A\backslash \left( A\cap B \right) \right)\cup \left( A\cap B \right)\cup \left( B\backslash \left( A\cap B \right) \right) \right)

2. The events A\backslash \left( A\cap B \right) , \left( A\cap B \right) and \left( B\backslash \left( A\cap B \right) \right) are disjoint, therefore, according to Axiom 3, I can write that:

P\left( A\cup B \right)=P\left( A\backslash \left( A\cap B \right) \right)+P\left( A\cap B \right)+P\left( B \backslash \left( A\cap B \right) \right)

3. Event A\cap B is contained in event A as well as in event B . According to the formula (property) already proven above (V) that can be written:

P\left( A\cup B \right)=P\left( A\right)-P\left( A\cap B \right)+P\left( A\cap B \right)+P\left( B \right)-P\left( A\cap B \right)

4. When tidying up, I get the formula:

P\left( A\cup B \right)=P\left( A\right)+P\left( B \right)-P\left( A\cap B \right)

which I was suppose to prove.

That’s all, as can be seen from the relatively “modest” definition, many interesting formulas and properties can be derived.

Please write me in the comments about your questions and doubts related to probability and formulas for them 🙂

Click here to return to the main Probability page