
Równania wielomianowe czwartego stopnia w liczbach zespolonych
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Przy rozwiązywaniu zadań z równań wielomianowych zespolonych stosujemy generalnie te same metody, co w rozwiązywaniu zadań z równań wielomianowych rzeczywistych w szkole średniej.
Równania zespolone czwartego stopnia sprowadzalne do drugiego stopnia
Dotyczy to także równań zespolonych 4 stopnia sprowadzalnych do równań stopnia 2, czyli takich, w których mamy niewiadomą do 4 potęgi, niewiadomą do 2 potęgi i wyraz wolny, na przykład:
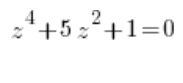
albo:
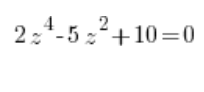
Tego typu równania zespolone sprowadzamy do równań zespolonych stopnia drugiego poprzez podstawienie ![]() , gdzie
, gdzie ![]()
![]()
Zadanie
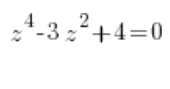
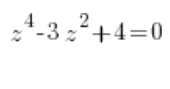
Podstawiamy ![]()
![]()
![]()
![]()
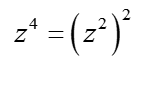
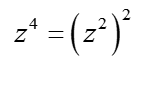
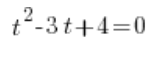
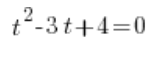
A to równanie rozwiązujmy więc już normalnie deltą (oczywiście pierwiastki z liczb ujemnych w liczbach zespolonych istnieją). Dostaniemy dwa rozwiązania zespolone:
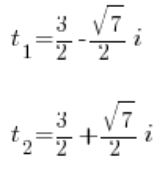
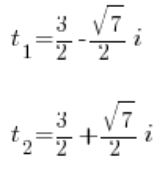
Skoro podstawiliśmy: ![]()
![]()
![]()
![]()
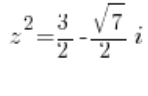
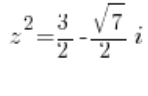
lub:
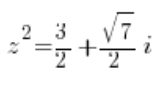
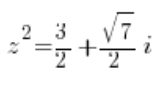
czyli:
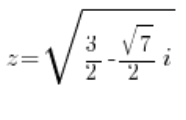
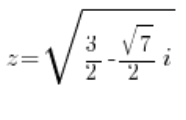
lub:
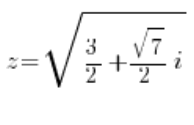
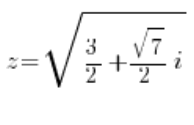
Po policzeniu pierwiastków (oczywiście wyjdą cztery pierwiastki zespolone) będziemy mieli cztery rozwiązania:
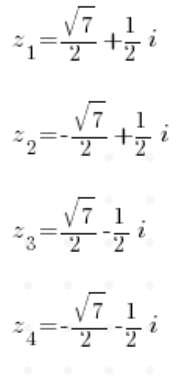
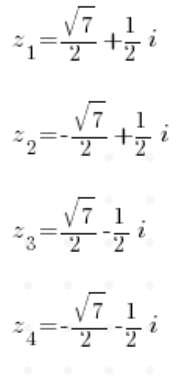
P.S. Tę i inne metody pokazuję w Lekcji 6 moje Kursu Liczby Zespolone, zapraszam!
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










z^3+2z^2+3z+2=0 jak rozwiązać takie zdanie
Można tak:
{z^3} + 2{z^2} + 3z + 2 = 0
{z^3} + 2{z^2} + z + 2z + 2 = 0
z\left( {{z^2} + 2z + 1} \right) + 2z + 2 = 0
z{\left( {z + 1} \right)^2} + 2\left( {z + 1} \right) = 0
(z + 1)\left[ {z\left( {z + 1} \right) + 2} \right] = 0
(z + 1)\left( {{z^2} + z + 2} \right) = 0
czyli:
z + 1 = 0 lub: {z^2} + z + 2 = 0
Z pierwszego równania mamy pierwszy pierwiastek z=-1.
Drugie rozwiązujemy jak zwykłe równanie kwadratowe:
{z^2} + z + 2 = 0
\Delta = {\left( { – 1} \right)^2} – 4 \cdot 1 \cdot 2 = 1 – 8 = – 7
\sqrt \Delta = \sqrt { – 7} = \sqrt { – 1} \cdot \sqrt 7 = \pm i\sqrt 7
{z_1} = \frac{{ – 1 – i\sqrt 7 }}{2} = – \frac{1}{2} – i\frac{{\sqrt 7 }}{2}
{z_2} = \frac{{ – 1 + i\sqrt 7 }}{2} = – \frac{1}{2} + i\frac{{\sqrt 7 }}{2}
Jak podejść do takiego zadania. Jak utworzyć wielomian stopnia czwartego o współczynnikach rzeczywistych i wyznaczyć wszystkie jego pierwiastki w dziedzinie zespolonej
jak
i
osiągnięto te 4 pierwiastki. Z jakich wzorów skorzystano
a jak by się pan dobrał do takiego przykładu?
z^5=i|z|^2
Krystian nie mogę sobie poradzić z takim zadaniem: z^4+ (1+2i)z^2-1+i=0. Czy byłbyś w stanie je rozwiązać?
Jeżeli połączymy rozkład który podałem \left(x^2+ax+bright)\left(x^2-ax+cright)=x^4+px^2+qx+r
z przypadkiem opisanym przez Krystiana to powinniśmy sobie poradzić z każdym równaniem czwartego stopnia
Krystian.. w swoim kursie nie wspomniałeś o przypadku , kiedy mamy równianie w zbiorze liczb zespolonych tego przypadku : iz^2+iz-2j=0 , jak postępować wtedy ?
Nakręciłem filmik, bardzo proszę:
Dodajac ze jednym z jego pierwiastkow jest liczba z1=-i-1
Nie mogę poradzić sobie z rozwiązaniem tego wielomianu; /
W(z)=z^4+2z^3+3z^2+2z+2
Witam czy mogłabym prosić o rozwiązanie następującego przykłądu:
Oblicz Im [(1-i)] e^(3-4i)]^26
Pozdrawiam!
Witam czy mogłabym prosić o rozwiązanie następującego przykłądu:
Oblicz Im [(1-i) e^3-4i[/latex]]^26[/latex]
Witam, a z czego jest “liczona” wartość urojona Im? Co jest podniesione do 26 potęgi? Bo w formule jest jeden nawias kwadratowy otwarty i dwa domknięte… ?
Do poczytania
http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1110.pdf
@Krystian mógłbyś coś napisać o funkcjach symetrycznych (tych wielu zmiennych)
Pamiętasz jakiś efektywny sposób wyrażania funkcji symetrycznych przez funkcje symetryczne podstawowe
(zgadywanie jakie funkcje pomnożyć a jakie odjąć średnio działa)
Jak później dobrać pierwiastki
Jeszcze słówko o równaniach trzeciego stopnia
Równanie trzeciego stopnia można rozwiązać sprowadzając je odpowiednimi podstawieniami do równania kwadratowego
Można też po wyeliminowaniu wyrazu x odpowiednim podstawieniem skojarzyć postać równania ze wzorem na sinus bądź cosinus kąta potrojonego
Podstawienie
x=y-\frac{a_{2}}{3a_{3}}
sprowadza równanie do postaci
y^3+py+q=0
Teraz mamy do wyboru kilka podstawień
y=u+v
Po tym podstawieniu dostajemy równanie które można łatwo przekształcić w układ równań
który będzie przypominał wzory Viete równania kwadratowego
Gdy równanie kwadratowe ma zespolone pierwiastki (casus irreducibilis) korzystamy ze wzoru de Moivre
i wyrażamy pierwiastki za pomocą funkcji trygonometrycznych
y=u-\frac{p}{3u}
Tutaj równanie kwadratowe otrzymujemy prawie zaraz po podstawieniu , trzeba jednak uważać na zerowe pierwiastki równania kwadratowego
y=2\sqrt{-\frac{p}{3}}cos{\theta}
Tutaj sprowadzamy równanie do równania które przypomina wzór na cosinus kąta potrojonego
Przykłady
@Krystian moze przydaloby sie przypomniec / dac odnosniki do tematow ktore uzytkownik powinien sobie przyswoic
poczawszy od wzorow skroconego mnozenie przeksztalcania rownan
dokonywania zamiany zmiennych ,twierdzenia Bezout, wzorow Viete
do podstawowych wiadomosci o liczbach zespolonych ,rownan drugiego i trzeciego stopnia
Rownanie czwartego stopnia mozna zapisac w postaci
(x^2+ax+b)(x^2-ax+c)=x^4+px^2+qx+r
Po wymnozeniu trojmianow i porownaniu wspolczynnikow
dostajemy uklad rownan ktory mozna sprowadzic do rownania trzeciego stopnia
Rownanie czwartego stopnia mozna tez zapisac w postaci
(x^2+b_1x+b_0)^2-p(x-c_0)^2=x^4+a_3x^3+a_2x^2+a_1x+a_0
Po wymnozeniu i porownaniu wspolczynnikow takze dostajemy rownanie trzeciego stopnia
Rownanie czwartego stopnia mozemy zapisac w postaci roznicy kwadratow tez w ten sposob
grupujemy rownanie w dwa nawiasy pomiedzy ktorymi stawiamy zmak minus
w pierwszym nawiasie umieszczamy wyrazy z x^4 oraz z x^3 a w drugim trojmian kwadratowy
uzupelniamy wyrazenie w pierwszym nawiasie do kwadratu dodajac do wyrazen w obu nawiasach odpowiedni wyraz zgodnie ze wzorem skroconego mnozenia na kwadrat sumy/roznicyponiewaz w drugim nawiasie jest trojmian kwadratowy wiec bedzie kwadratem gdy jego wyroznik bedzie rowny zero
aby ustalic kiedy wyroznik trojmianu bedzie rowny zero trzeba wprowadzic nowa zmienna (gdybysmy od razu liczyli wyroznik trojmianu to mogloby sie okazac ze nie jest on zerowy )
wprowadzamy nowa zmienna tak aby wyrazenie w pierwszym nawiasie nadal bylo kwadratem (znowu dodajemy do wyrazen w obu nawiasach odpowiednie wyrazy zgodnie ze wzorem skroconego mnozenia na kwadrat sumy)
po przyrownaniu wyroznika trojmianu do zera otrzymujemy
rownanie trzeciego stopnia wzgledem wprowadzonej zmiennej
rozwiazujemy rownanie trzeciego stopnia i wybieramy jeden pierwiastek
i wstawiamy go do rownania czwartego stopnia
teraz gdy rownanie czwartego stopnia przybralo postac roznicy kwadratow
korzystamy ze wzoru skroconego mnozenia na roznice kwadratow
i otrzymujemy iloczyn dwoch trojmianow kwadratowych
Rownania czwartego stopnia nie trzeba rozkladac na czynniki kwadratowe
poniewaz dziala na nie takze pomysl na rownanie trzeciego stopnia
Mariusz, dzięki za bardzo wartościowego posta.
Jesteś pewien, że w tym układzie równań skończy się na trzecim stopniu równania? Bo mi coś tak nie bardzo wychodzi. Nie chciało by Ci się rozpisać to np. na jakimś przykładzie, zrobić foto kartki z obliczeniami i np. przesłać mi na maila (bo tyle obliczeń kodowanych w stylu: x^2 to straszna mordęga)?
Dzięki! Bardzo dobrze wytłumaczone, a wspomnij jeszcze tutaj o wzorze:
pierwiastki:
cz. rzeczywista: -b/2a
cz. urojona: [sqrt(delta)*i] / 2a
i \sqrt(delta) = i \sqrt(4ac – b^2)
Dzięki, ale nie znam tego wzoru:) Na co on? Na pierwiastki równania wielomianowego 4go stopnia sprowadzalne do drugiego? Mógłbyś podrzucić jakiś przykład, jak on działa?