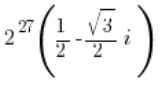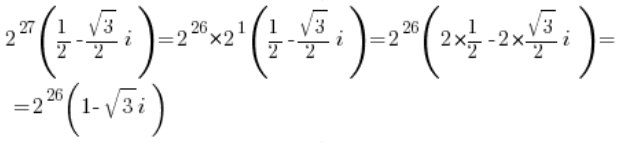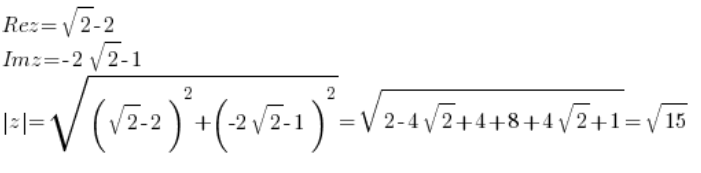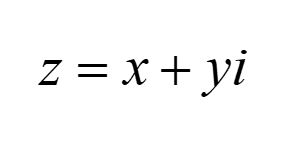
Pomocne „myki” w liczbach zespolonych
Krystian
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka koło Szczecina. Lubi spacery po lesie, plażowanie i piłkę nożną.
Liczby zespolone jako całość nie są tematem skomplikowanym i trudnym. „Gorąco” może się w nich jednak zrobić w sytuacjach nietypowych i mniej schematycznych. Kluczem jest wtedy – jak zawsze – zrozumienie tematu i „chłodna głowa”, czyli przytomność umysłu i pewność siebie.
Przykłady
Na przykład:
- Po podniesieniu liczby zespolonej do jakiejś bardziej sporawej potęgi często wychodzimy na trochę dziwny twór typu:
Aby poprawić estetykę liczby, można tu wykonać następujące przekształcenie:
Poprawa estetyki jest często bardzo ważna – szczególnie jeśli ta liczba jest częścią jakiegoś jeszcze bardziej skomplikowanego matematycznego stwora. - Liczba zespolona w postaci kartezjańskiej (inaczej: algebraicznej) nie musi być wcale taka ładna, jak na przykład:
. Równie dobrze jej część rzeczywista i urojona może być brzydką, niewymierną paskudą, taką jak:
Bez paniki jednak, jest to zwykła liczba zespolona, w której (cześć rzeczywista nie przemnożona przez 'i', część urojona przemnożona):
– zmiana znaku w części urojonej
Jedna z wielu opinii o naszych Kursach...
Nigdy nie byłem dobry z matmy a wybrałem się na studia inżynierskie, teraz zaczynam wszystko rozumieć. Jednak nauczyciel ma znaczenie!Paweł
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
