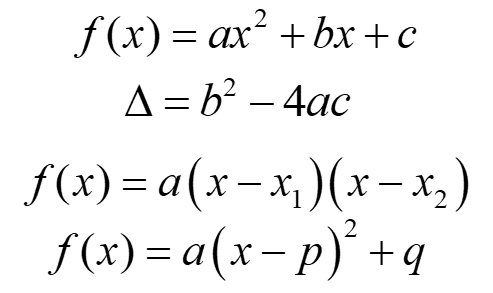
Kilka Rzeczy, Których Powinieneś Się Dobrze Nauczyć w Średniej, Ale Nikt Ci Tego Nie Powiedział – część 3 Funkcja kwadratowa
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Ten post to już trzeci z kolei post, w którym chciałbym zwrócić Ci uwagę na rzeczy, które warto powtórzyć sobie na samym początku nauki matematyki na studiach. Ich szybka powtórka bardzo ułatwi Ci życie na studiach. W poprzednich postach poruszyłem tematy:
Interpretacji geometrycznej wartości bezwzględnej
Dzisiaj kolej na funkcję kwadratową.
Funkcja kwadratowa? Ale myśmy to chyba przez dwa miesiące robili…
Temat funkcji kwadratowej jest oczywiście bardzo szeroki i nie chodzi mi w ogóle o to, żeby brać podręcznik ze średniej i przerabiać cały rozdział od deski do deski.
Skupmy się tylko na kilku istotnych szczegółach, niuansach i pułapkach.
Funkcja kwadratowa a równanie kwadratowe
Funkcja kwadratowa to oczywiście coś takiego:
![]() albo:
albo: 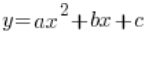
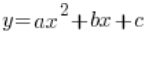
Gdzie ![]()
![]()
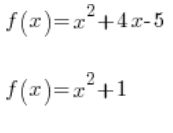
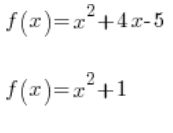
itd…
Pojęcie funkcji kwadratowej należy odróżniać od pojęcia równania kwadratowego, na przykład:
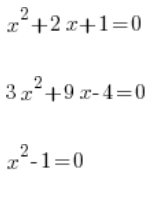
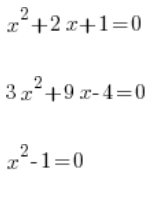
itd…
To nie to samo!!!!
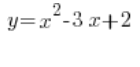
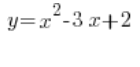
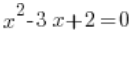
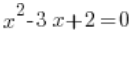
Z nierozróżniania funkcji od równania bierze się częsty na studiach…
Makabryczny błąd numer 1
Licząc na przykład pochodne i mając daną funkcję:
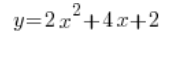
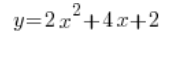
Ludzie często robią coś takiego:
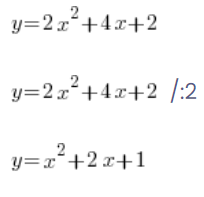
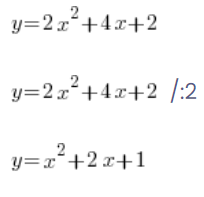
…i liczą sobie dalej co tam potrzeba.
Mylą się tak, ponieważ pamiętają, że można było robić coś takiego na równaniach:
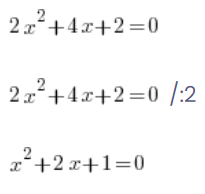
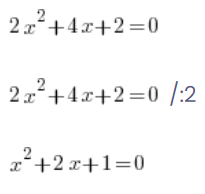
…i na równaniu wszystko jest O.K., można podzielić obustronnie, 0 po prawej podzielone przez 2 daje faktycznie 0 i równania są równoważne (mają takie same rozwiązania).
Tego numeru nie można jednak wykonywać na funkcjach – trzeba by przecież chyba jakoś też ten y po lewej podzielić itd. Po zwykłym podzieleniu wartości funkcji przez 2 otrzymamy inną funkcję!
Co trzeba sobie powtórzyć z funkcji?
Nie tak wiele. Właściwie tylko dwie postaci funkcji: kanoniczną i iloczynową.
Postać kanoniczna funkcji kwadratowej
Zakładam, że postać ogólną funkcji kwadratowej już mamy:
![]()
![]()
![]()
![]()
Jej postać kanoniczna to:
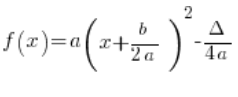
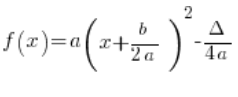
Czyli:
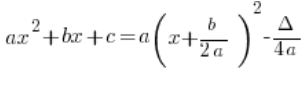
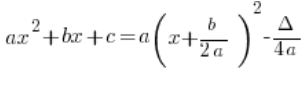
Co to jest a,b i ![]()
![]()
![]()
![]()
![]()
Można nawet zauważyć, że jeśli w postaci kanonicznej wyciągniemy ![]()
![]()
![]()
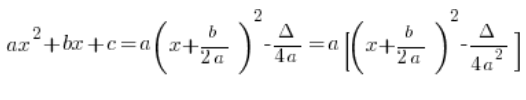
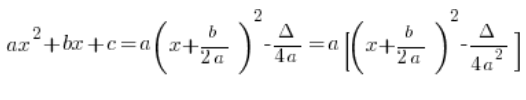
…co czasami może się przydać, a czasami niekoniecznie.
Jesli uczyłeś się tego licząc na boku współrzędne wierzchołka (zwykle jako ![]()
![]()
![]()
![]()
![]()
![]()
Pamiętaj o ![]()
![]()
![]()
Postać iloczynowa funkcji kwadratowej (jej rozkład na czynniki):
Wracając teraz do naszej ogólnej funkcji kwadratowej:
![]()
![]()
![]()
![]()
Bardzo często trzeba będzie “rozłożyć ją na czynniki”, wykorzystując w tym celu postać iloczynową funkcji kwadratowej:
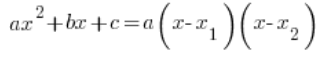
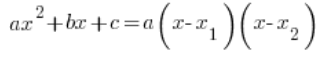
Gdzie ![]()
![]()
![]()
![]()
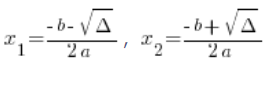
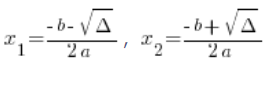
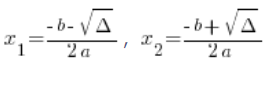
Tutaj również musisz pamiętać o ![]()
![]()
Zauważ także, że te ![]()
![]()
![]()
![]()
Co trzeba sobie powtórzyć z równań kwadratowych?
Z równaniami kwadratowymi jak przypuszczam nie jest najgorzej. Raczej radzimy sobie z rozwiązaniem ogólnego równania:
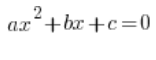
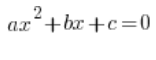
Na przykład:
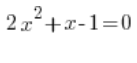
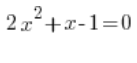
Liczymy po prostu:
![]()
![]()
![]()
A potem, jeśli delta wyszła nieujemna rozwiązania równania:
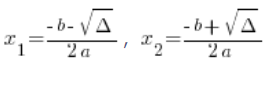
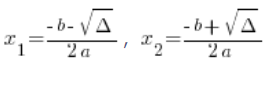
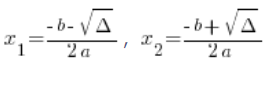
Pamiętaj, że tam na dole w mianownikach jest ![]()
![]()
Chciałbym jednak zatrzymać się na przypadku szczególnym równania:
![]()
![]()
![]()
Tutaj dochodzi do wielu błędów. Na przykład:
Makabryczny błąd numer 2
![]()
![]()
![]()
![]()
![]()
![]()
Na czym polega błąd właściwie? Liczba 2 jest rzeczywiście rozwiązaniem równania ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Rozwiązanie ujemne można pomijać tylko w geometrii (bo odległość nie może być ujemna).
Inny problem z równaniem w postaci: ![]()
![]()
![]()
Makabryczny błąd numer 3
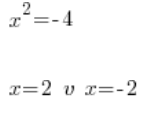
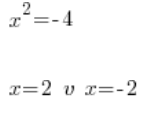
Co jest oczywiście bzdurą, bo 2 do kwadratu nie daje -4. W ogóle nic do kwadratu nie daje -4 (Ci którzy mieli już liczby zespolone niech siedzą cicho). Równanie:
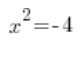
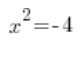
…nie ma w ogóle rozwiązań.
Trzeba więc być czujnym. Równanie ![]()
![]()
![]()
![]()
Zapraszam do spokojnego powtórzenia sobie tego wszystkiego, co było powiedziane do tej pory i oczywiście do pytań w komentarzach.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Witam, witam.
Normalnie się od tej strony nie mogę odkleić ale to takie pozytywne:)
Jak moje studia? Do przodu. Brakuje mi co prawda matematyki jako przedmiotu w tym roku, ale będzie się przewijać przez inne przedmioty. Mamy teraz dużo laboratoriów. Od czasu do czasu wracam do list z zadaniami, żeby sobie odświeżyć niektóre rzeczy.
Powodzenia dla wszystkich, którzy będą się z matematyką zmagać w tym roku na studiach. W razie problemów macie Pana Krystiana.
Poleciłem Pana kursy studen\tom na mojej uczelni:)
Pozdrawiam
To powodzenia, dzięki i pozdrawiam.
Witam Panie Krystianie.
Fajne te ostatnie artykuły. Szczególnie do szybkiej powtórki. A jeżeli komuś NAPRAWDĘ tęskno do tej funkcji kwadratowej… Pozostaje podręcznik a w nim takie cuda jak np. rodziny parabol…
Autora poprzedniego posta zapytał Pan o studia. Chyba nikt nie weźmie mi tego za złe, jak napiszę troszkę o swoich. Pierwszy, jedyny, wymarzony kierunek studiów – MATEMATYKA, którą od dawna się \interesowałem. Przerabiałem materiał ze studiów, żeby mi było lżej, byłem na etapie równań różniczkowych… A poszedłem na Administrację. Jednak… do Królowej Nauk z pewnością jeszcze wrócę w przyszłości. 😉 A na obecnym kierunku – to więcej prawa niż tej administracji…
Dobra nie będę się za bardzo rozpisywał, bo bym musiał pół życia opisać, a poza tym – jest już późno (dochodzi pierwsza w nocy) 😛
Pozdrawiam.
Mateusz
Jeszcze PRZED rozpoczęciem studiów przerobił Pan materiał aż do równań różniczkowych?
Respect 🙂
Administracja to szlachetny kierunek, niech Pan studiuje z dumą 🙂
Pozdrawiam
Krystian
Nic do kwadratu nie daje -4? Hmmm.. dobrze będę siedział cicho hihi:D Widzę, że działa Pan na blogu bez przerwy. Bardzo fajnie, że powstają takie wpisy jak te 3 ostatnie:) Wpadłem, żeby zobaczyć co słychać. Pozdrawiam
Pozdrawiam, dzięki za komentarz. A jak tam studia?
pierwiastki oznacza się x1 oraz x2 a nie znów x1. oczywiście jest to Pana małe przeoczenie, które jest zrozumiałe,lecz może nie dla wszystkich.nie pisze bo się czepiam, lecz ktoś kto słabo zna materiał pomyśli ze dwa razy piszemy x1. napisze tak w szkole i nauczyciel się będzie czepiał.
Racja, dzięki, że Pan zwrócił na to uwagę.