Model ekonometryczny jako podstawa ekonometrii

---

Ekonometria Wykład 2

Temat: Model ekonometryczny

 

We wcześniejszym Wykładzie 1 starałam się przedstawić czym jest oraz czym zajmuje się ekonometria.

Jak każda z dziedzin ekonomicznych, czy też matematycznych, ma swoje podstawowe narzędzia wykorzystywane do badań zależności ilościowych. Tym praktycznym narzędziem jest właśnie model ekonometryczny.

W tym artykule spróbuję to pojęcie rozłożyć na czynniki pierwsze.

No to jedziemy.

 

Pojęcie modelu ekonometrycznego

Jak już wspomniałam na wstępie, podstawowym narzędziem wykorzystywanym w analizie ekonometrycznej jest model ekonometryczny.

“Model” to formalna konstrukcja teoretyczna, która podlega analizie w miejsce rzeczywistego zjawiska. To takie jakby uproszczone odwzorowanie rzeczywistości. Pisząc “uproszczone” mam na myśli uwzględnienie w modelu tylko najistotniejszych elementów rzeczywistości, a pominięcie tych mniej ważnych. Tutaj chyba się ze mną zgodzisz, bo przecież nie jesteśmy w stanie wziąć pod uwagę wszystkich, ale to wszystkich możliwości.

Przykład 1

Pan Janusz od kilku lat prowadzi komis samochodowy. Postanowił wyjaśnić, od czego zależy wartość sprzedaży znajdujących się tam samochodów. Analizując uważnie wszystkie możliwości, doszedł do zaskakujących dla niego wniosków. Nigdy by nie pomyślał, że sprzedaż samochodów zależy od tak wielu czynników: cena (oczywiste), ale również marka samochodu, jego wiek, przebieg, stan techniczny, czy był powypadkowy, kraj pochodzenia, jego kolor, liczba poprzednich właścicieli, ilość ogłoszeń w prasie, ilość ogłoszeń w Internecie, liczba wypadków w mieście, pora roku sprzedaży, wydatki na reklamę komisu, ilość dni deszczowych, ilość dni śnieżnych oraz mroźnych…

Mógłby tak jeszcze wyliczać i wyliczać. 

Gdyby Pan Janusz chciałby zbudować z tego model wyjaśniający sprzedaż, to czy na prawdę musiałby uwzględniać te wszystkie dane? Oczywiście, że nie do końca byłoby to sensowne.

Jak pewnie zauważasz, wpływ jednych zmiennych  jest silny i trwały. Inne są słabsze i nietrwałe. Do tego trzeba uwzględnić wpływ tzw. czynników losowych – nagłych, nieregularnych, ale mających istotny wpływ (np. kradzież kilku samochodów z komisu).

 

Wracając do pojęcia modelu ekonometrycznego. Bardzo precyzyjną definicję ułożył polski ekonometryk, Zbigniew Pawłowski:

“Model ekonometryczny jest to konstrukcja formalna, która za pomocą pewnego równania, lub układu równań przedstawia zasadnicze powiązania występujące pomiędzy rozpatrywanymi zjawiskami ekonomicznymi.”

Zatem jest to równanie, czyli pewien zapis matematyczny, który został „dopasowany” do rzeczywistości za pomocą odpowiednich metod statystycznych. Ważne – uwzględnia się w nim tylko najistotniejsze zmienne.

 

Tak wygląda najbardziej ogólna postać modelu:

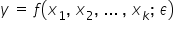
Z czego się składa? Ma kilka stałych elementów:

a) Po pierwsze, zmienną którą chcesz objaśnić za pomocą modelu. Nazywana jest po prostu “zmienną objaśnianą”. Najczęściej oznaczana jest jako “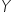” i znajduje się po lewej stronie równania. Bardzo często nazywana jest też “zmienną zależną” (bo istnieją zmienne od których ona zależy, które mają na nią wpływ).

W naszym przykładzie jako 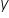 można uznać “wartość sprzedaży samochodów”.

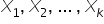
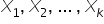
b) Kolejnym elementem jest zmienna lub zmienne, którymi chcesz WYJAŚNIĆ zachowanie zmiennej objaśnianej.  Tutaj to już przyda się Twoja własna wiedza, plus niewielkie doświadczenie i trochę wyobraźni. Tak jak Pana Janusza, który tych zmiennych znalazł aż kilkanaście. Najczęściej oznaczane są kolejno:  . Są to „zmienne objaśniające”, bo służą własnie do objaśniania. Znajdują się po prawej stronie równości. Nazywane są też również “zmiennymi niezależnymi”, gdyż one już od niczego nie zależą; mają własną, ustaloną treść ekonomiczną.

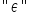
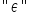
c) W zapisie widzisz taką dziwną literkę , takie jakby ładnie ręcznie napisane „E”. Jest to epsilon, litera grecka. Ona z kolei oznacza zmienną losową, tzw. „składnik losowy”, czy też “zakłócenie losowe”.

Równanie matematyczne zawsze traktujemy jako przybliżoną wartość. Dlatego też składnik losowy uwzględnia m.in.: różnice między modelem a rzeczywistością; wpływ innych zmiennych niż te, które są już w modelu; błędy pomiaru zmiennych; czy też działanie czynników losowych, niespodziewanych.

Więcej o tym polecam poczytać w następnym Wykładzie. Sam się przekonasz, że jest on bardzo ważnym elementem modelu.

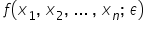
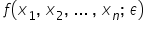
d) Funkcja  jest zapisem typu związku funkcyjnego między zmienną objaśnianą, a zmiennymi objaśniającymi, oraz składnikiem losowym.

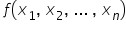
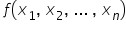
Chodzi tu o to, w jaki sposób “połączone” są ze sobą zmienne. Czy liniowo, czyli jakby dodawane, a może jakoś ze sobą mnożone? Może wartości wybranej zmiennej warto wyrazić jako logarytm? Oczywiście funkcja , która opisuje powiązania między zmiennymi objaśniającymi może być dowolna (wykładnicza, logarytmiczna, wymierna, mieszanka kilku na raz…). Tutaj wybór masz nieograniczony.

Kilka pokazowych funkcji: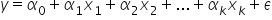 

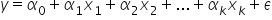
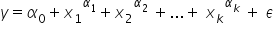
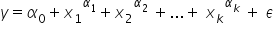
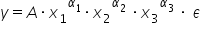
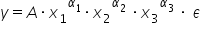
e) Jak widzisz na powyższych przykładach, oprócz , oraz , występują jeszcze inne literki. Tutaj akurat oznaczone jako . Są to pewne skalary, czyli wartości liczbowe, przez które dana zmienna jest pomnażana. Nazywane są “parametrami strukturalnymi“. Oczywiście możesz użyć dowolnych literek, nawet po prostu . Jednak najczęściej w takim ogólnym zapisie modelu ekonometrycznego spotkasz się z greckimi literkami (alfa, beta, gamma itd…).

 

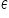
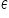
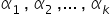
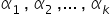
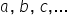
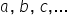
Gdybyśmy chcieli zbudować jakiś prosty model ekonometryczny dla pana Janusza (z Przykładu 1), mógłby wyglądać on np. tak:

Przyjęłam (dla uproszczenia późniejszych obliczeń) liniową zależność między zmiennymi.

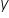
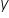
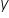
Specjalnie nie wypisałam tutaj wszystkich cech wymienionych przez Pana Janusza. Nie miałoby to sensu. Tak zbudowany model byłby po prostu zbyt rozległy. To raz. Po drugie nie zawsze uwzględnienie wielu zmiennych jest wskazane. Teoretyczne wartości dla zmiennej objaśnianej , wyliczone na postawie modelu, byłyby prawdopodobnie zbyt odległe od tych rzeczywistych wyników sprzedaży. Model po prostu nie będzie wtedy “dobrze dopasowany” do zmiennych ekonomicznych.

O co chodzi z tym “dopasowaniem” modelu do danych, opowiem w kolejnych Wykładach.

 

Jeszcze wspomnę (może akurat przyda Ci się to na egzamin), że ekonometrycy wyróżniają dwa typy charakteru modelu ekonometrycznego, w zależności od tego, czy uwzględniany jest w nim tzw. “składnik losowy” czy też nie. Dlatego jest on dosyć ważnym jego elementem.

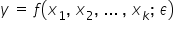
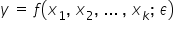
MODELE STOCHASTYCZNE – modele uwzględniające składnik losowy, czyli   . Są to modele spotykane chyba w  przypadków.

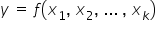
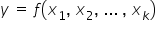
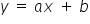
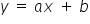
MODELE DETERMINISTYCZNE – modele nie uwzględniające składnika losowego, czyli   . Jest to najzwyklejsza konkretna funkcja, np. dobrze Ci znana linia prosta .

Skąd ta różnica? Składnik losowy zawiera m.in. wszystkie zmienne pominięte, czy też błędy w pomiarach i obliczeniach. Ta własność jest jakby “bliższa” rzeczywistym zmiennych, temu co się na prawdę dzieje w realnym świecie. Przecież nigdy nie jesteśmy w stanie określić idealnie wprost “funkcyjnych” zależności.

Dlatego też należy pamiętać, że wnioskowanie na podstawie modelu stochastycznego, po oszacowaniu jego parametrów ma tylko przybliżony charakter.

 

Skoro już wiemy jak wygląda nasz model, zostaje nam tylko zebranie odpowiednich danych, ułożenie modelu, oszacowanie go (czyli wyliczenie konkretnych wartości liczbowych dla parametrów strukturalnych), weryfikacja i zastosowanie. Czyli kolejne etapy modelowania ekonometrycznego.

Zachęcam Cię do poczytania moich kolejnych Wykładów oraz zapoznania z moim Kursem.

 

KONIEC

---

Kliknij, aby powtórzyć sobie, czym jest ekonometria (poprzedni Wykład) <–

Kliknij, aby poznać rolę składnika losowego w modelu ekonometrycznym (następny Wykład) ->

Kliknij, aby powrócić na stronę z Wykładami do ekonometrii

---