Kalkulator Do Całek Nieoznaczonych (Sprawdź, Czy Dobrze Liczysz)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Przedstawiam Wolframow’y kalkulator do całek nieoznaczonych, przerobiony troszkę przeze mnie:
Sprawa jest prosta: w kalkulator wpisujemy formułę (zgodnie z Zasadami) – bez dx, klikamy na ‘Oblicz’ i mamy policzoną całkę.
Na przykład, żeby policzyć \int{\frac{{{x}^{2}}}{{{x}^{2}}+1}}dxwpisujemy w kalkulator: x^2/(x^2+1).
Tyle, mam nadzieję, że kalkulator się Tobie przyda. W razie kłopotów z jego korzystaniem, daj znać w komentarzach pod postem.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.









Potrzebuję pomocy z całką nieoznaczoną: całka to sin^3 x-1/sin^2 x dx
Potrzebuję pomocy z całką oznaczoną: granice całkowania od -1 do 1 całka to : (2-t^2)^(1/2)
dziękuję za pomoc, a jak by wyszło z tą całką?
∫(2x-3)^7 dx
Z tą najlepiej przez podstawienie:
\int {{{\left( {2x – 3} \right)}^7}dx} = \left| \begin{array}{l}
t = 2x – 3\\
dt = 2dx\\
dx = \frac{{dt}}{2}
\end{array} \right| = \int {{t^7}\frac{{dt}}{2}} = \frac{1}{2}\int {{t^7}dt} = \frac{1}{2}\frac{1}{{7 + 1}}{t^{7 + 1}} + C =
= \frac{1}{2} \cdot \frac{1}{8}{t^8} + C = \frac{1}{{16}}{t^8} + C = \frac{1}{{16}}{\left( {2x – 3} \right)^8} + C
Bardzo dziękuję za pomoc
proszę o pomoc
∫(x^2 √x-√x)/x dx
Pójdzie tak:
\int {\frac{{{x^2}\sqrt x – \sqrt x }}{x}dx} = \int {\left( {\frac{{{x^2}\sqrt x }}{x} – \frac{{\sqrt x }}{x}} \right)dx} = \int {\left( {\frac{{{x^2}{x^{{\textstyle{1 \over 2}}}}}}{x} – \frac{{{x^{{\textstyle{1 \over 2}}}}}}{x}} \right)dx} =
= \int {\left( {\frac{{{x^{2 + {\textstyle{1 \over 2}}}}}}{x} – {x^{{\textstyle{1 \over 2}} – 1}}} \right)dx} = \int {\left( {\frac{{{x^{{\textstyle{5 \over 2}}}}}}{x} – {x^{ – {\textstyle{1 \over 2}}}}} \right)dx} = \int {\left( {{x^{{\textstyle{5 \over 2}} – 1}} – {x^{ – {\textstyle{1 \over 2}}}}} \right)dx} =
= \int {\left( {{x^{{\textstyle{3 \over 2}}}} – {x^{ – {\textstyle{1 \over 2}}}}} \right)dx} = \int {{x^{{\textstyle{3 \over 2}}}}dx} – \int {{x^{ – {\textstyle{1 \over 2}}}}dx} = \frac{1}{{1 + {\textstyle{3 \over 2}}}}{x^{1 + {\textstyle{3 \over 2}}}} – \frac{1}{{1 – {\textstyle{1 \over 2}}}}{x^{1 – {\textstyle{1 \over 2}}}} + C =
= \frac{1}{{{\textstyle{5 \over 2}}}}{x^{{\textstyle{5 \over 2}}}} – \frac{1}{{{\textstyle{1 \over 2}}}}{x^{^{{\textstyle{1 \over 2}}}}} + C = 1 \cdot \frac{2}{5}{x^{{\textstyle{5 \over 2}}}} – 1 \cdot \frac{2}{1}\sqrt x + C = \frac{2}{5}{x^{{\textstyle{5 \over 2}}}} – 2\sqrt x + C
Jak obliczyć całkę?
(sqrt{3}(x^2)-2x^4+1/x)/(3x^2)
Jak zbadać zbieżność całki niewłaściwej od 0 do plus nieskończoności z wyrażenia:(x/pierwiastek z(x^2+1))-1 ?
Witam, dlaczego całka z e^-x wynosi -e^-x?
Można to pyknąć przez podstawienie:
\int {{e^{ – x}}dx} = \left| \begin{array}{l}
t = – x\\
dt = – dx\\
dx = – dt
\end{array} \right| = \int {{e^t}\left( { – dt} \right)} = – \int {{e^t}dt} = – {e^t} + C = – {e^{ – x}} + C
Witam mam problem z rozwiązaniem całki, jakiej metody mam użyć w pierwszym przykładzie? przez podstawienie?
1. (2x-4)lnxdx
2. e^x/e^2x +4( tylko 2x jest w potędze, 4 poza)
Pozdrawiam
Witam,
1. Przez części.
2. Przez podstawienie.
Witam, usiłuję rozwiązać zadanie 26 z zadania domowego z lekcji numer 2 z kursu dotyczącego całek nieoznaczonych. Czy może Pan wyjaśnić ten przykład:
całka 2^x/pierwiastek(1-4^x). Z
Z góry dziękuję za pomoc
Witam, dostałem na kolokwium taką całkę, męczę ją niestety już od tygodnia i nie potrafię jej rozwiązać, czy mógłbym prosić o pomoc? Całka jest następująca: (1 – arctg^9x) *dx / (1 + x^2) * arctgx
Z góry bardzo dziękuję 🙂
Witam. Taką całkę możemy bardzo łatwo rozwiązać przez podstawienie. Mamy:
\displaystyle\int\frac{1-\operatorname{arctg}^9 x}{(1+x^2)\operatorname{arctg} x}\,dx =\begin{vmatrix}t=\operatorname{arctg}x\\dt=\frac{1}{1+x^2}\,dx\end{vmatrix}=\int\frac{1-t^9}{t}\,dt=\int\frac{1}{t}\,dt-\int t^8\,dt=\ln{|t|}-\frac{1}{9}t^9+C=\ln{|\operatorname{arctg}x|}-\frac{1}{9}\operatorname{arctg}^9 x+C .
Mam problem z jednym z zadań, mogę prosić o pomoc ?
Calka 1/5*cos(x)*sin(x)^2
Z tego co kojarzę to wynik wynosi 2/15
Mam problem z obliczeniem całki
1-x^3/x-1
Proszę o pomoc 🙂
Żeby rozłożyć wyrażenie z licznika, skorzystamy ze wzoru na różnicę sześcianów:
a^3 – b^3 = (a-b)(a^2 + ab + b^2) .
Mamy:
\displaystyle\int\frac{1-x^3}{x-1}\,dx=\int\frac{(1-x)(1+x+x^2)}{x-1}\,dx=\int\frac{(1-x)(1+x+x^2)}{-(1-x)}\,dx=\int -(1+x+x^2)\,dx= -x-\frac{1}{2}x^2-\frac{1}{3}x^3+C .
Próbuję obliczyć całkę 2x+7/x^3-16x po dx.
Sposób rozwiązywania tego typu całek przedstawiłem w moim Kursie Całek Nieoznaczonych.
Pójdzie tak:
Próbuję obliczyć całkę (arcsinx)^2, proszę o pomoc
Pójdzie tak:
Czy umie ktoś policzyć tę całkę
Proszę o pomoc
Jak obliczyć całkę? (x+9)/(x^3+2x^2+3x)
Proszę o pomoc.
Dokładną metodę liczenia całek wymiernych pokazałem tutaj:
https://online.etrapez.pl/lesson/lekcja-5-calki-wymierne/
Zastosujmy ją do tego konkretnego przykładu:
W mianowniku mamy wyższy stopień wielomianu niż w liczniku. Mianownik można rozłożyć na czynniki, bo jest stopnia nieparzystego (3). Zgodnie więc z rozpiską:
Dalej nie da się rozłożyć, bo delta trójmianu kwadratowego jest ujemna:
Ułamek rozkładamy na ułamki proste:
Czyli:
Cdn. 🙂
cd.
Dzień dobry.
Czy mógłby ktoś policzyć taką całkę:
Z góry dziękuję.
Pozdrawiam Mariusz
Dzień Dobry
Czy ktoś zna rozwiązanie poniższej całki nieoznaczonej
sinx/(1+3x)
Dzień dobry. Czy mógłby ktoś pomóc mi z tą całką? Mam ją całkować przez części, ale nie wychodzi mi i nie wiem jak obliczyć:
Całka x^2e^x sinxdx
Witam nie mogę dać sobie rady z całka
(Cos2x/√x^7)dx
Proszę o pomoc
Pozdrawiam
((s^2)+6,5*(10^4)*s+0,5*(10^8)-0,5*(10^4)*s)((s^5)+6,5*(10^4)+(s^4)+0,5*(10^8)*(s^3))
czemu nie mogę tego policzyć???
Dzień dobry , pomógł by ktoś z taką całeczką, z góry dziękuje
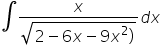
Dzień dobry
Jedziemy zgodnie ze schematem pokazanym w tej Lekcji.
Liczymy pochodną tego pod pierwiastkiem w mianowniku:
Doprowadzamy część składników licznika do tej pochodnej:
Rozbijamy całkę na dwie:
Obie te całki liczymy osobno:
Sprowadzamy dwumian w mianowniku do postaci
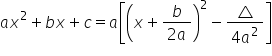
Podstawiamy
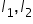
Witam mam problem z calka 1/cosx mogłbys mi ja rozpisac? zgory dziekuje i pozdrawiam
Jak obliczyc calke (1 na gorze 0 na dole) adalej (3x^3-x^2+2x-4)dx/((x^2-3x+2)^0,5)gdyby sie udalo krok po kroku zebym mogla rozumiec logikepozdrawiamJoanna
Aby rozwiązać całkę
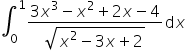
Jest to całka typu
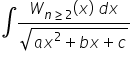
Musze teraz znaleźć niewiadome A, B , C oraz lambdę. No i oczywiście rozwiązać całkę z pierwiastkiem. Na powyższe równanie nakładam obustronnie pochodną. Przy obliczaniu pochodnej z wyrażenia
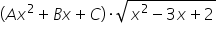

Porządkuję prawą stronę i porównuję potęgi przy odpowiednich x-ach wielomianu.
Tak więc na obecną chwilę mamy rozwiązanie postaci:
Zostaje więc do policzenia tylko całka z pierwiastkiem

CDN.
Kończąc przykład, całka



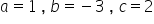
Zapisuję wielomian z mianownika w postaci:
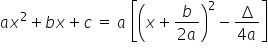
Liczę:
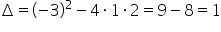
Korzystając z wzoru na całkę:
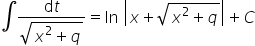
Dlatego ostateczna całka z przykładu jest postaci:
Dziwić może różniący się wynik otrzymany z kalkulatora, tzn.
Wydawałoby się, że to wyrażenie w logarytmie jest inne. Nic mylnego. Wolfram to chytra sztuka i zawsze próbuje wynik maksymalnie “uładnić” 🙂 Po prostu dobrał sobie taką stałą i wciągnął ją do logarytmu, aby pozbyć się ułamka, tzn:
gdzie ln|-2| to zwykła stała, podlegająca pod “C”.
To została do policzenia całka oznaczona.
Jak obliczyć y’-y*sinx=sinx*cosx.
Czy da się to zadanie wpisać w kalkulator?
Da się wpisać w kalkulator, tyle, że w inny, do równań różniczkowych:
https://blog.etrapez.pl/narzedzia/kalkulatory/kalkulator-do-rownan-rozniczkowych/
A obliczyć można stosując metodę “uzmienniania stałej”, pokazałem ją w swoim Kursie dokładniej:
Rozwiązuję odpowiadające temu równaniu równanie jednorodne:
W otrzymanym rozwiązaniu równania jednorodnego “uzmienniamy stałą”, a następnie liczymy pochodną:
Otrzymane wyniki wstawiamy do równania na początku:
Całeczkę rozwiązuję najpierw przez podstawienie, potem przez części:
Mam więc, że:
Wstawiam ten wynik do rozwiązania z uzmiennioną stałą:
Co jest rozwiązaniem tego równania różniczkowego.
Witam, mam problem z wyznaczeniem obszaru ograniczonego przez:y=|cosx| , x=0 , x=3/2*

Witam, mam problem z wyznaczeniem obszaru ograniczonego przez:y=|cosx|x=0x=3/2

Obliczyć całkę z funkcji e^{x^2}. Jak?
Witam
Mam problem z całka nieoznaczoną
2x-9/3\pirwiastki z 3
Mianownik to zwykła liczba (nie ma tam zmiennej “x”). Dlatego wyciągam go jako stałą przed całkę. Dalej to proste działania na całkach elementarnych.
Witam mam problem z niektórymi przykładami całkowania przez podstawienie, mógłby ktoś mi je rozpisać? 1.
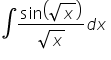

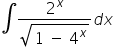


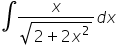
Całka nr 1: (pójdzie przez podstawienie)
Dokładny sposób postępowania omówiono w Kursie Całki Nieoznaczone. Pierwsza lekcja (całki bezpośrednie) dostępna jest za darmo po założeniu konta na Akademii.
Całka nr 2 także pójdzie przez podstawienie i wykorzystanie bezpośredniego wzoru
oraz małe przekształcanie
(1/2-sinx)^2 pomoże mi ktoś przy tej całce ?
Chodzi o całkę:
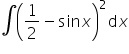
Najpierw korzystam ze wzoru skróconego mnożenia:
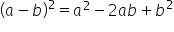
Pierwsze dwie całki są proste:
Zostaje trzecia całka z
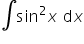
https://online.etrapez.pl/lesson/lekcja-7-calki-trygonometryczne/
Należy skorzystać tu z przekształcenia dodatkowej zależności funkcji trygonometrycznych, mianowicie
Podstawiam to teraz do całki z sinusem kwadrat
Wykorzystano tu bezpośredni wzór z dodatkowych wzorów (lub tez można było to obliczyć szybką całką przez podstawienie
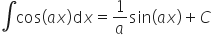
Ostatnie wychodzi:
Hej :)pomoże ktoś obliczyć:
Mam problem z taką oto całką: (x-13)/(x^3-x-6) dx mianownik ni jak da się rozłożyć – zatem zgodnie ze schematem muszę przekształcić licznik tak, aby był podobny do mianownika – tylko co jeśli się nie da jak tutaj?? HELP 🙂
a co z taką całką? Całka: 2x/(x-1)^8 dx ?
Ta całka pójdzie tak:
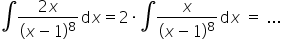
rozbijam ułamek na sumę dwóch ułamków. Na dole jest aż 8 potęga, ja nie potrzebuję rozbijać na osiem kolejnych ułamków, gdzie w mianowniku będą kolejne potęgi wyrażenia (x-1)… Wystarczy że zejdę tylko o JEDEN stopień niżej, ponieważ w liczniku jest tylko “x” (postać liniowa wielomianu, x w pierwszej potędze), czyli:
Każdą z całek liczę na boku, przez podstawienie:
Wracając do całki:
A pomoże ktoś w takiej całeczce: ln(2x+3)/2x+3
Całka
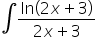
Witam, posiadam całkę(cos(x/5))/((sin^8(x/5)jak ją obliczyć metodą przez podstawianie t= sin(x/5)
co oznacza ei
Dzien dobry, mam problem z rozwiązaniem poniższej całki… Nie mam kompletnie pomysłu jak się za to zabrać, próbowałam przez części jak i przed podstawienie, ale niestety do nieczego mądrego nie doszłam…
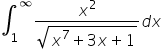
Czy ktoś ma pomysł jak rozwiązać poniższą całkę? Męczę się już dość długo z nią i wszystkie pomysły na jej rozwiązanie doprowadzają mnie do ślepego zaułku.
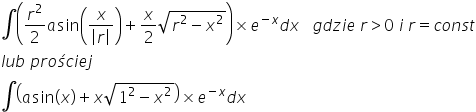
Dzień dobry,mam problem z całką z funkcji
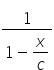

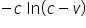

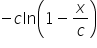
Witam, mam problem z całką (x^2)(sinx)^2 z zadania domowego nr 10 z lekcji 4. Wynik wychodzi mi podobny ale na końcu zamiast -(1/4)xcox2x+(1/8)sin2x mam -(1/2)xcos2x+(1/4)sin2x, tak jakbym coś zgubił po drodze, a liczyłem kilka razy i ciągle ten sam wynik. Ktoś coś?
Całka przez podstawienie : sin2x/
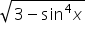
Przez podstawienie: całka x^2/
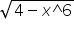
Jak obliczyć całkę: 5x^2-6x+12/x^4-2x^3+4x^2
pomocy całka 4^x/2^x
Tutaj wyjdzie ostatecznie prosta całka, trzeba tylko na samym początku dokonać kilku przekształceń:
Proszę o rozpisanie tych całek są to przykłady z kursu pana Krystiana. Piszę ponieważ nie mogę ich rozgryźć i dojść do zgodności z wynikiem końcowym.Całka nieoznaczona
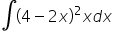

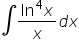

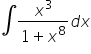

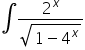
Pozostałe całki:
20)
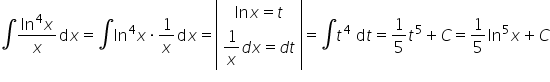
25)
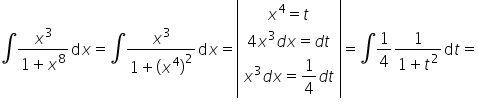

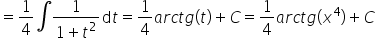
26)
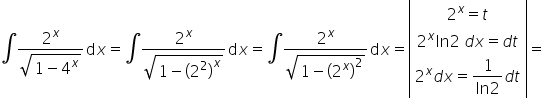

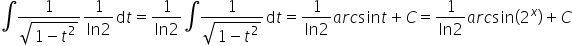
Dzień dobry…. bardzo proszę o pomoc w rozwiązaniu całki …:cosx/(sinx^3+sinx^2)… 🙁
Dzień dobry 🙂 Wstałam jaki sposób obliczyć całkę z (1+x)^x
Witam mam pytanie jak obliczyc calke x^2/(3x^2-6)^(1/3)
Witam,jak rozwinąć całkę od A (x^2)dA ?
t=2-x^2dt=2xdxdt/2=xdx
Witam mam problem z całką 1/x(x^2-2)^1/2 dx. Jak ją rozwiązać?
Proszę o pomoc część już zrobiłem ale potem się zatrzymałem
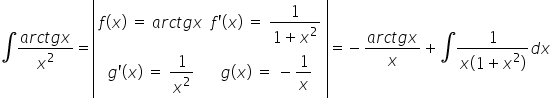
Już rozwiązałem 🙂
Witam, proszę o pomoc w wyliczeniu jednej całki:
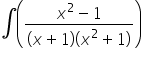
Proszę bardzo, tutaj rozwiązanie tej całeczki: 🙂
a najprostrza całka: (5+7x-3x^2)dx? 🙁
Tutaj wystarczy rozbić to na sumę 3 całek i wykorzystać podstawowe wzory:
Stąd:
Witam! Jak mam wpisać pierwiastek TRZECIEJ potęgi? Potrzebuję całkę z 3x^4 + 4*pierwiastek z 3 potęgi z x + \sqrt( x) / x Serdecznie dziękuję
Pierwiastek trzeciego stopnia najlepiej wpisywać z potęgą ułamkową, tzn
Czyli w Pani przypadku liczona całka to:
3x^4 + 4*(x)^1/3 + \sqrt( x) / x
Wersja 1.
Wersja 2.
Witam
Czy aby na pewno o taką całkę chodzi? W tej postaci nawet Wolfram wyrzuca, że nie można jej policzyć metodami elementarnymi.
Pozdrawiam
Mam problem z całką oznaczoną i m.in. równaniami z nimi nie wiem jak się za nie zabrać proszę o wsparcie
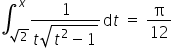
Na początku oczywiście należy wyliczyć podaną całkę. Można to zrobić przez podstawienie
Dalej powracamy do całki oznaczonej
gdzie w ostatniej równości skorzystano z faktu, że
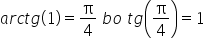
Tym samy równanie
sprowadzamy do postaci
Rozwiązując dostaniemy
witam, mam problem z całkami : 1 )
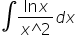

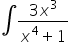

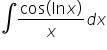

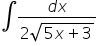
1)
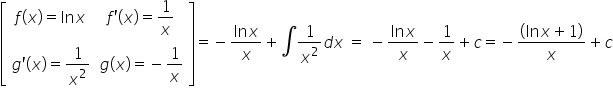


3)
Proszę o pomoc 🙁 całka z 2^x*sin3x dx
Niech
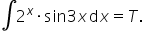
Witam, mam problem z przeliczeniem całki
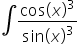
Wersja 1.
Wersja 2.
Tej całki nie da się rozwiązać w funkcjach znanych.
Witam, bardzo proszę o pomoc w rozwiązaniu całki z (1 + (2*sinx*cosx)^2)^(1/2) dx
Witam, prosze o pomoc w rozwiązaniu zadania 17 z lekcji 2 z całek nieoznaczonych. sin(2 x^1/2)/x^1-2 dx
Zastosujemy tu całkowanie przez podstawienie:
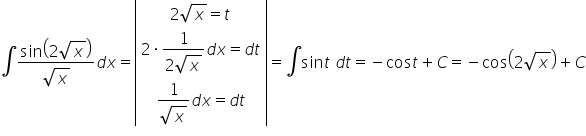
Witam, bardzo proszę o pomoc w rozwiązaniu całki z (x^4 – 1)/(x-1) dx.
Z góry bardzo dziękuję 🙂
Tę całkę wymierną
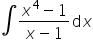
Witam. Proszę o pomoc z trudną dość całką.
(1/x)*sinx Chodzi mi o wartości w punktach pi/2 oraz 0 (dla x=0 jak się nie mylę jest 0)
mam Problem z całką cosx/(sin^3x+sinx) czy byłby mi ktoś w stanie pomóc? Proszę
Wyznaczymy teraz rozkład na ułamki proste wyrażenia pod całką:
W kalkulatorze całek wychodzi wynik:
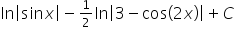
Oba te wyniki są ze sobą tożsame. Można dokonać następujących przekształceń:
gdzie
pan jest boski <3
Witam czy mógłby ktoś mi pomoc z rozwiazaniem całki x^3ln(x^2+3)
Całkuję przez części:
Rozpisuję na boku całkę wymierną:
Dzielę licznik przez mianownik pisemnie:
Wracając do całki wymiernej:
Bo jedna z całek została obliczona przez podstawienie
Mam więc ostatecznie:
witam mam do rozwiązania dwie calki:)
1 calka to : ln^2x/x
2 calka to: (x^2-2)/(x^2+1)
czy ktoś pomoze?
Całka pierwsza: \displaystyle \int{{\frac{{{{{ln }}^{2}}x}}{x}}}dx
\displaystyle \int{{\frac{{{{{ln }}^{2}}x}}{x}}}dx=\left| {\begin{matrix} t=ln x \ dt=\frac{1}{x}dx \end{matrix}} \right|=\int{{{{t}^{2}}}}dt=\frac{1}{3}{{t}^{3}}+C=\frac{1}{3}{{ln }^{3}}x+C
Całka druga: \displaystyle \int{{\frac{{{{x}^{2}}-2}}{{{{x}^{2}}+1}}}}dx
\displaystyle \int{{\frac{{{{x}^{2}}-2}}{{{{x}^{2}}+1}}}}dx=\int{{\frac{{{{x}^{2}}+1-3}}{{{{x}^{2}}+1}}}}dx=\int{{\left( {\frac{{{{x}^{2}}+1}}{{{{x}^{2}}+1}}-\frac{3}{{{{x}^{2}}+1}}} \right)}}dx=
\displaystyle =\int{{1dx-3\int{{\frac{1}{{{{x}^{2}}+1}}}}}}dx=x-3\cdot arctgx+C
zapis w kalkulatorze calek log(x) to jest logarytm naturalny czy dziesiętny??
log(x) oznaczany jest przez WolframAlpha jako logarytm naturalny.
Logarytm przy podstawie dziesiętnej to log_10(x) .
dzieki
Wydaje mi się ze kalkulator zle liczy calki z f wymiernych. np takie \integral 1/((x^2+1)(x^2+4))
wychodzi mi (1/3) arctgx +(-1/6) arctg(x/2) przy czym kalkulator daje mi w wyniku 2/x
sprawdzałem w wolframie wszystko i rozbicie na ulamki proste i pojedyncze calki z tych ulamkow i suma ich była rozna niż calka z całej f wymiennej. Jakies wskazówki? Dziekuje 😉
Rozwiązanie:
Najpierw przedstawiamy ten ułamek jako sumę ułamków prostych:
Odejmując od trzeciego równania pierwsze, otrzymamy:
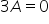


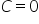

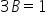

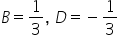
W takim razie,
(Oczywiście, ten samy wynik można było otrzymać szybciej w sposób trochę stuczny:
Wracamy do całki i liczymy ją, korzystając ze wzoru:
Mamy:
Witam. mam do policzenia objętość bryły. Mam obliczyć objętość bryły utworzonych przez obrót dookoła osi OX krzywych: y=1-x^2 i y=x^2+2.
Witam Panie Krystianie! mam problem z jedną całką a mianowicie (1+e^x)^(1/2) proszę o pomoc w środę mam egzamin.
Zastosujemy tu całkowanie przez podstawienie wraz z pewnymi przekształceniami:
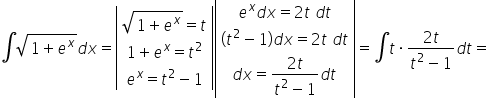

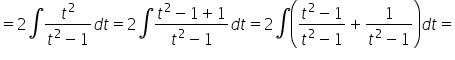

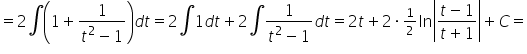

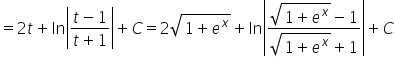

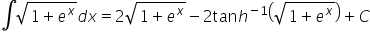

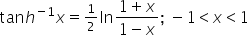
Cześć jak byś miał chwile i rozpisał mi jak rozwiązać całkę z xcos(5x) , liczę juz 3 strony i końca nie widać.
Zastosujemy tu całkowanie przez części:
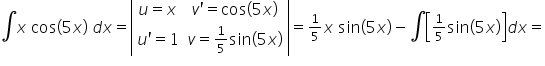

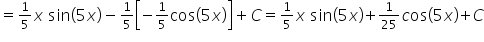

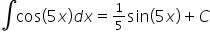

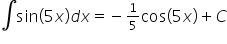
Nie mogę rozwiązać przykładu 21 z zadania domowego całek nieoznaczonych wymiernych, czyli
(8x^3)/(x+1)^4.
Proszę o pomoc
dobra, nieważne. Juz zrobilem 😀
Mamy do obliczenia następującą całkę:
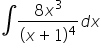
Zastosujemy tutaj rozkład na ułamki proste.
mam problem z taką całką: a^-x dx. Mógłbyś mi pomóc, nie korzystajac z Wolframa?
Rozwiązanie:
Liczymy to przez podstawienie:
Np, dla a=2 mamy:
mam problem : oblicz funkcje pierwotna f(x)=ln(x+1)
Zastosujemy tu całkowanie przez części.
Mam problem z rozwiązaniem całki z 1 lekcji przykład 18 z zadania domowego: 4-x^2/x√x , mogę prosić o pomoc w rozwiazaniu ?
Zastosujemy całkowanie przez podstawienie. Można ułatwić sobie podnosząc obustronnie
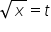

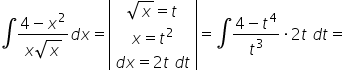

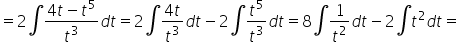

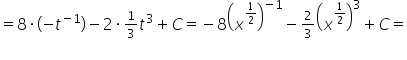

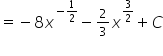
Witam
Mam problem z całką z dx/(4 + 3sinx). Zgodnie z poleceniem muszę ją rozwiązać przy pomocy podstawienia tg(x/2) = t. Takim sposobem dochodzę do całki z dt/(2(t^2) + 3t + 2). W tym miejscu zaczynają się problemy, bo w rozwiązaniu jest wynik: (2/(7^1/2))*arctg((4t+3/(7^1/2)). Mi natomiast wychodzi ((7^1/2)/2) * arctg((4t+3/(7^1/2)). Nie mam pojęcia czy to ja robię błąd, czy może podana odpowiedź jest nieprawidłowa. Proszę o pomoc!!
Z góry dzięki wszystkim, pozdrawiam.
Rozwiązanie:
prosze o pomoc w obliczeniu całki z e^(x^2) dziękuję z góry
Mam problem z całkami prosiabym o rozwiązanie:
(2x^-1,2+3x^-0,8-5x^0,4)
x+2x^2/pierwiastek 3stopnia z x
x^2*e^4x^3-7
x^3ln
osttania całka ma być
x^3lnx
Mam problem z taką całką √x/(√x-1)
Całkę
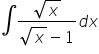

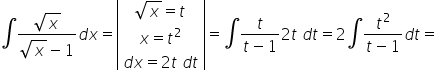

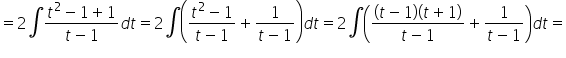

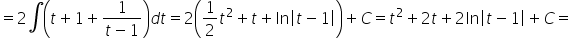

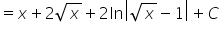
Witam. Mam problem z całką z nr3 z lekcji piątej 🙁 x/(x^2 + 1/2x – 3/16)
Mamy do obliczenia całkę
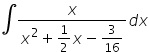

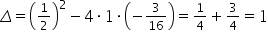

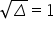

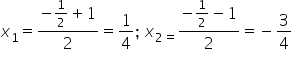

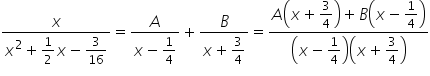

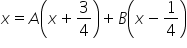

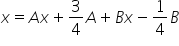

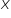

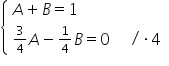

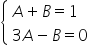

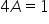

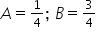

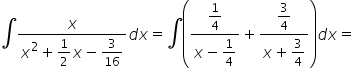

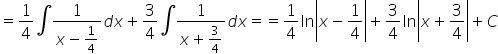
potrzebna mi całka cbrt{0,00027698913*(x^5+3x^4+3x^3+3x^2)}
Witam, mógłby mi ktoś pomóc z całką (2^x)/((1-4^x)^1/2)??
Witam,
Mam problem z policzeniem całki z zadania domowego:
e^(x^1/3)
Będę wdzięczna za pomoc.
Pozdrawiam
Całka nr 13 z Zadania Domowego Lekcja 4:
\int {{e}^{{\sqrt[3]{x}}}}~dx=\int {{e}^{{{{x}^{{\frac{1}{3}}}}}}}~dx[/latex]
Najpierw stosuję podstawienie:
\int {{e}^{{{{x}^{{\frac{1}{3}}}}}}}~dx=| {\begin{matrix} {{x}^{{\frac{1}{3}}}}=t \\ \frac{1}{3}{{x}^{{-\frac{2}{3}}}}dx=dt~~~/\cdot 3{{x}^{{\frac{2}{3}}}}~~ \\ dx=3{{x}^{{\frac{1}{3}\cdot 2}}}dt=3{{t}^{2}}dt \end{matrix}} |=\int 3{{t}^{2}}{{e}^{t}}~dx~~=~~
Obliczam całkę przez części:
=3\int {{t}^{2}}\cdot {{e}^{t}}~dx~~=| {\begin{matrix} u={{t}^{2}} & v’={{e}^{t}} \\ u’=2t & v={{e}^{t}} \end{matrix}} |=3\left[ {{t}^{2}}\cdot {{e}^{t}}-\int 2t\cdot {{e}^{t}}~dx \right]=3{{t}^{2}}{{e}^{t}}-6\int t\cdot {{e}^{t}}~dx=….
Ponownie stosując całkowanie przez części rozwiązuję otrzymaną całkę:
\int t\cdot {{e}^{t}}~dx~~=| {\begin{matrix} u=t & v’={{e}^{t}} \\ u’=1 & v={{e}^{t}} \end{matrix}} |=t\cdot {{e}^{t}}-\int 1\cdot {{e}^{t}}~dx=t{{e}^{t}}-\int {{e}^{t}}~dx=t{{e}^{t}}-{{e}^{t}}~+C
Wracam do mojej pierwotnej całki:
….=3{{t}^{2}}{{e}^{t}}-6\left[ {t{{e}^{t}}-{{e}^{t}}~+C} \right]=~3{{t}^{2}}{{e}^{t}}-6t{{e}^{t}}+6{{e}^{t}}~+C~=
I do postawienia z początku t={{x}^{{\frac{1}{3}}}}=\sqrt[3]{x}[/latex] , dzięki czemu mam wynik:
=\mathbf{3}{{\left( {\sqrt[\mathbf{3}]{\mathbf{x}}} \right)}^{\mathbf{2}}}{{e}^{{\sqrt[\mathbf{3}]{\mathbf{x}}}}}-\mathbf{6}\left( {\sqrt[\mathbf{3}]{\mathbf{x}}} \right){{e}^{{\sqrt[\mathbf{3}]{\mathbf{x}}}}}+\mathbf{6}{{e}^{{\sqrt[\mathbf{3}]{\mathbf{x}}}}}+C
Mam problem z takim działaniem:
całka w granicach od – nieskończoności do 0 z 0 x dx + całka o tych samych granicach z e^x dx. Bardzo proszę o pomoc.
Witam! Panie Krystianie mam problem z taką całką: całka w granicach od -100 do 100 z x^20 arctgx dx.
Witam ja nie umiem policzyc calki 26 z zadania domowego calki nieoznaczone wstep mecze sie z nia i mecze (x^2-1)/(x-1) mozna prosic o pomoc?
Witam, tak, jasne, proszę bardzo:
\int{\frac{{{x}^{2}}-1}{x-1}dx}=\int{\frac{\left( x-1 \right)\left( x+1 \right)}{x-1}dx}=\int{\left( x+1 \right)dx}=\int{xdx}+\int{dx}=\frac{1}{2}{{x}^{2}}+x+C
Witam, mam problem z całką (zastosowanie całek) opisaną y=1/(sqrt[3](x-1)) x=0 x=9 y=0. Dziękuję z góry za pomoc
Witam,
Mamy ten komfort, że obędzie się bez wykresu. Granice całkowania są z góry dane, x od 0 do 9, czyli mamy:
\int\limits_{0}^{9}{\frac{1}{\sqrt[3]{x-1}}dx}[/latex]
Całka jest podstępna, bo udaje “zwykłą” oznaczoną, a tak naprawdę jest niewłaściwa. x=1nie należy do dziedziny. Całkę rozbijamy więc na dwie:
\int\limits_{0}^{9}{\frac{1}{\sqrt[3]{x-1}}dx}=\int\limits_{0}^{1}{\frac{1}{\sqrt[3]{x-1}}dx}+\int\limits_{1}^{9}{\frac{1}{\sqrt[3]{x-1}}dx}[/latex]
Liczę osobno pierwszą całkę:
\int\limits_{0}^{1}{\frac{1}{\sqrt[3]{x-1}}dx}=\underset{\varepsilon \to {{1}^{-}}}{\mathop{lim }}\int\limits_{0}^{\varepsilon }{\frac{1}{\sqrt[3]{x-1}}dx}=\ldots [/latex]
\int{\frac{1}{\sqrt[3]{x-1}}dx}=\left| \begin{matrix}
& t=x-1 \\
& dt=dx \end{matrix} \right|=\int{\frac{1}{\sqrt[3]{t}}dt}=\int{{{t}^{-\tfrac{1}{3}}}dt}=\frac{1}{\tfrac{2}{3}}{{t}^{\tfrac{2}{3}}}+C=\frac{3}{2}\sqrt[3]{{{t}^{2}}}+C=\frac{3}{2}\sqrt[3]{{{\left( x-1 \right)}^{2}}}+C[/latex]
\underset{\varepsilon \to {{1}^{-}}}{\mathop{lim }} [ \frac{3}{2}\sqrt[3]{{{\left( x-1 \right)}^{2}}} ] |_{0}^{\varepsilon }=\underset{\varepsilon \to {{1}^{-}}}{\mathop{lim }}\left( [ \frac{3}{2}\sqrt[3]{{{\left( \varepsilon -1 \right)}^{2}}} ]-[ \frac{3}{2}\sqrt[3]{{{\left( 0-1 \right)}^{2}}} ] \right)=\frac{3}{2}\cdot 0-\frac{3}{2}\cdot 1=-\frac{3}{2}[/latex]
Potem liczę osobno drugą całkę:
\int\limits_{1}^{9}{\frac{1}{\sqrt[3]{x-1}}dx}=\underset{\varepsilon \to {{1}^{+}}}{\mathop{lim }}\int\limits_{\varepsilon }^{9}{\frac{1}{\sqrt[3]{x-1}}dx}=\ldots [/latex]
\underset{\varepsilon \to {{1}^{+}}}{\mathop{lim }} \left[ \frac{3}{2}\sqrt[3]{{{\left( x-1 \right)}^{2}}} \right] |_{\varepsilon }^{9}=\underset{\varepsilon \to {{1}^{+}}}{\mathop{lim }} \left( \left[ \frac{3}{2}\sqrt[3]{{{\left( 9-1 \right)}^{2}}} \right]-\left[ \frac{3}{2}\sqrt[3]{{{\left( \varepsilon -1 \right)}^{2}}} \right] \right)=\frac{3}{2}\cdot 4-\frac{3}{2}\cdot 0=6[/latex]
Wracam się do “głównej” całki i mam:
\int\limits_{0}^{9}{\frac{1}{\sqrt[3]{x-1}}dx}=\int\limits_{0}^{1}{\frac{1}{\sqrt[3]{x-1}}dx}+\int\limits_{1}^{9}{\frac{1}{\sqrt[3]{x-1}}dx}=-\frac{3}{2}+6=4\tfrac{1}{2}[/latex]
Witam, czy można prosić o pomoc z całka [ (x^1/2 + 2x) (3-x) ] / x^3 ? poprzez wymnożenie i podział z właściwości całek wychodzi dalej dzielenie przez 0, a kalkulator nie mam pojęcia skąd to policzył. Dzięki z góry
Witam cały przykład krok po kroku pójdzie tak:
\int{\frac{\left( \sqrt{x}+2x \right)\left( 3-x \right)}{{{x}^{3}}}dx}=\int{\frac{3\sqrt{x}-x\sqrt{x}+6x-2{{x}^{2}}}{{{x}^{3}}}dx}=
=\int{\left( \frac{3\sqrt{x}}{{{x}^{3}}}-\frac{x\sqrt{x}}{{{x}^{3}}}+\frac{6x}{{{x}^{3}}}-\frac{2{{x}^{2}}}{{{x}^{3}}} \right)dx}=\int{\left( \frac{3{{x}^{\tfrac{1}{2}}}}{{{x}^{3}}}-\frac{{{x}^{\tfrac{3}{2}}}}{{{x}^{3}}}+\frac{6}{{{x}^{2}}}-\frac{2}{x} \right)dx}=
=\int{\left( 3{{x}^{-2\tfrac{1}{2}}}-{{x}^{-\tfrac{3}{2}}}+6{{x}^{-2}}-\frac{2}{x} \right)dx}=3\int{{{x}^{-2\tfrac{1}{2}}}dx}-\int{{{x}^{-\tfrac{3}{2}}}dx}+6\int{{{x}^{-2}}dx}-2\int{\frac{1}{x}dx}=
=3\frac{1}{-2\tfrac{1}{2}+1}{{x}^{-2\tfrac{1}{2}+2}}-\frac{1}{-\tfrac{3}{2}+1}{{x}^{-\tfrac{3}{2}+1}}+6\frac{1}{-2+1}{{x}^{-2+1}}-2ln \left| x \right|+C=
=3\left( -\frac{2}{3} \right){{x}^{-\tfrac{3}{2}}}+2{{x}^{-\tfrac{1}{2}}}-6{{x}^{-1}}-2ln \left| x \right|+C=-2{{x}^{-\tfrac{3}{2}}}+2{{x}^{-\tfrac{1}{2}}}-6{{x}^{-1}}-2ln \left| x \right|+C=
=-\frac{2}{\sqrt[3]{{{x}^{2}}}}+\frac{2}{\sqrt{x}}-\frac{6}{x}-2ln \left| x \right|+C[/latex]
Domyślam się, że problem z dzieleniem przez zero wynikł przy okazji liczenia całki \int{\frac{1}{x}dx}. Nie można do niej zastosować wzoru: \int{{{x}^{n}}dx}=\frac{1}{n+1}{{x}^{n+1}}+C.
Ten wzór, co jest zaznaczone we wszystkich wzorach na całki, obowiązuje tylko dla nne 1.
Tutaj należy zastosować wzór: \int{\frac{1}{x}dx}=ln \left| x \right|+C.
Witam Panie Krystianie
Mam problem przy rozwiązaniu 9 całki z zadania domowego, dokładnie kurs całki oznaczone, niewłaściwe i zastosowania całek, jest to lekcja 2. Nie wiem co tam źle liczę, ale cały czas wychodzi mi 0, bardzo proszę o pilna pomoc obliczenia tego przykładu,
Pozdrawiam
Mamy do obliczenia całkę nieoznaczoną
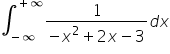
Zaczniemy od przekształcenia mianownika do postaci pozwalającej obliczyć tego typu całkę, zgodnie ze schematem obliczania całek wymiernych.
Wielomianu w mianowniku nie da się rozłożyć na czynniki liniowe. Przekształcamy zatem następująco:
Teraz obliczymy całkę nieoznaczoną zamieniając ją najpierw na sumę dwóch całek.
Mam problem z taką całką:
integral(e^(-2e^x))dx
Kalkulator daje wynik, ale to za mało. Ja pokonany, a zadanie z fizyki stoi :). Proszę o wsparcie.
Krystian jesteś najlepszy! dzięki Tobie zaliczam matme na spokojnie 🙂
potrzebuje pomocy z obliczeniem calki xsin4x
To pójdzie tak:
\int{xsin 4xdx}=\left| \begin{matrix}
u=x & {v}’=sin 4x \\
{u}’=1 & v=-\frac{1}{4}cos 4x \end{matrix} \right|=
=-\frac{1}{4}xcos 4x-\int{1\cdot \left( -\frac{1}{4}cos 4x \right)dx}=-\frac{1}{4}xcos 4x+\frac{1}{4}\int{cos 4xdx}=
=-\frac{1}{4}xcos 4x+\frac{1}{4}\cdot \frac{1}{4}sin 4x+C=-\frac{1}{4}xcos 4x+\frac{1}{16}sin 4x+C
Witam,
Proszę o rozwiązanie dla całki 3/(x^4)
\int{\frac{3}{{{x}^{4}}}dx}=3\int{\frac{1}{{{x}^{4}}}dx}=3\int{{{x}^{-4}}dx}=3\frac{1}{-4+1}{{x}^{-4+1}}+C=3\cdot \frac{1}{-3}{{x}^{-3}}+C=
=-\frac{1}{{{x}^{3}}}+C
Witam,
Poproszę o pomoc w rozwiązaniu całki oznaczonej [2,782*(1- exp(-0,125t)*cos(2,5t))]dt w granicach od 0 do 42.
z góry dziękuję 🙂
Witam 🙂 Mam problem z całką cos^2xsins^2x. proszę o pomoc 🙂 Pozdrawiam
Tutaj akurat da się zastosować taki sprytny “patent”, mianowicie skorzystać z trygonometrycznego wzoru ze średniej sin 2x=2sin xcos x:
\int{{{sin }^{2}}x{{cos }^{2}}xdx}=\int{{{\left( sin xcos x \right)}^{2}}dx}=\int{{{\left( \frac{1}{2}\cdot 2sin xcos x \right)}^{2}}dx}=
=\int{{{\left( \frac{1}{2} \right)}^{2}}\cdot {{\left( 2sin xcos x \right)}^{2}}dx}=\frac{1}{4}\int{{{\left( sin 2x \right)}^{2}}dx}=\frac{1}{4}\int{{{sin }^{2}}2xdx}=
Teraz korzystam z innego trygonometrycznego wzoru ze średniej (przerywając na chwilę liczenie całki):
cos 2x={{cos }^{2}}x-{{sin }^{2}}x
czyli:
cos 4x={{cos }^{2}}2x-{{sin }^{2}}2x
cos 4x=1-{{sin }^{2}}2x-{{sin }^{2}}2x
2{{sin }^{2}}2x=1-cos 4x
{{sin }^{2}}2x=\frac{1}{2}\left( 1-cos 4x \right)
Mając wyznaczony {{sin }^{2}}2xwracam się do całki:
\frac{1}{4}\int{{{sin }^{2}}2xdx}=\frac{1}{4}\int{\frac{1}{2}\left( 1-cos 4x \right)dx}=\frac{1}{8}\int{\left( 1-cos 4x \right)dx}=
=\frac{1}{8}\int{dx}-\frac{1}{8}\int{cos 4xdx}=\frac{1}{8}x-\frac{1}{8}\cdot \frac{1}{4}sin 4x+C=\frac{1}{8}x-\frac{1}{32}sin 4x+C
Witam! 🙂 Czy mogłabym prosić o wskazówkę, jak policzyć całkę przez podstawianie 1/(x^2-2x+2)? 🙂
Witam. Można tak:
\int{\frac{1}{{{x}^{2}}-2x+2}dx}=\int{\frac{1}{{{x}^{2}}-2x+1+1}dx}=\int{\frac{1}{{{\left( x-1 \right)}^{2}}+1}dx}=\left| \begin{matrix}
& t=x-1 \\
& dt=dx \end{matrix} \right|=
\int{\frac{1}{{{t}^{2}}+{{1}^{2}}}=arctgt+C}=arctg\left( x-1 \right)+C
…ale wszystko tutaj opierało się na sprytnym zauważeniu tego wzoru skróconego mnożenia. Bardziej uniwersalny schemat jest w moim Kursie Całek Nieoznaczonych na Lekcji 5 – zapraszam!
Dzień dobry, mam pytanie: jak wyliczyc calke z (lgx)/(x)?? DZIEKUJE
przez podstawienie
lnx=t
dt=1/x
i wtedy masz całkę z tdt czyli (x^2)/2 🙂
Witam, mam problem z całką nr 14 z zadania domowego z lekcji całkowanie przez podstawienie, nie bardzo wiem jakie ma być to podstawienie?
dokładnie chodzi o x^4(x^2+11)^1/2 dx
Tam nie ma na początku {{x}^{4}}, tylko jest xpomnożone przez pierwiastek CZWARTEGO stopnia, czyli całka wygląda tak (inaczej zapisana):
\int{x\cdot \sqrt[4]{4{{x}^{2}}+11}dx}[/latex]
🙂
a tak się męczyłam, dziękuję bardzo 🙂
witam, mam problem z całką z zadania domowego z lekcji 4 całek nieoznaczonych, dokładnie chodzi o przykład 15, w którym w mianowniku jest 3sinx^2-7cosx^2 i całosc pod pierwiastkiem. Nie mam pojęcia od czego zacząć tutaj, próbowałem podstawiania ale zapętlałem sie coraz bardziej, prosze o pomoc, pozdrawiam 🙂
to znaczy po kilku przeliczeniach wychodzi mi wynik rozbieżny z tym w odpowiedziach z tym że tyle sieróznie ułamkiem przed całoscia bo mi wychodzi 1/10 a u Pana w odpowiedzi ja mam -1/4, skąd może być ta rozbieżność?
Tak, tam był kiedyś błąd w odpowiedziach, powinna być 1/10, przepraszam!
Witam. Próbowałam wyliczyć całkę z przykładu 15, ale wychodzą mi całkiem inne wyniki, nie wiem jak się za to zabrać. Czy mógłby ktoś napisać mi jak powinno wyglądać podstawienie?
Powinno to pójść tak:
\int{\frac{sin xcos x}{\sqrt{3{{sin }^{2}}x-7{{cos }^{2}}x}}dx}=\left| \begin{matrix}
& t=3{{sin }^{2}}x-7{{cos }^{2}}x \\
& dt=6sin xcos x-14cos x\cdot \left( -sin x \right) \\
& dt=20sin xcos xdx \\
& \frac{dt}{20}=sin xcos xdx \end{matrix} \right|=
=\int{\frac{\tfrac{dt}{20}}{\sqrt{t}}}=\frac{1}{20}\int{\frac{dt}{\sqrt{t}}}=\frac{1}{20}\int{\frac{1}{{{t}^{\tfrac{1}{2}}}}dt}=\frac{1}{20}\int{{{t}^{-\tfrac{1}{2}}}dt}=\frac{1}{20}\cdot \frac{1}{\tfrac{1}{2}}{{t}^{\tfrac{1}{2}}}+C=\frac{1}{20}\cdot 2{{t}^{\tfrac{1}{2}}}+C=
=\frac{1}{10}\sqrt{t}+C=\frac{1}{10}\sqrt{3{{sin }^{2}}x-7{{cos }^{2}}x}+C
Witam Panie Krystianie
Mam problem z całką (2x-1)/(x-2)
Dziękuje za pomoc
\displaystyle \int{{\frac{{2x-1}}{{x-2}}}}dx
Na początku porządkuje wyrażenie pod całką:
\displaystyle \frac{{2x-1}}{{x-2}}=\frac{{2(x-2)+3}}{{x-2}}=\frac{{2(x-2)}}{{x-2}}+\frac{3}{{x-2}}=2+\frac{3}{{x-2}}
Liczę:
\displaystyle \int{{\frac{{2x-1}}{{x-2}}}}dx=\int{{\left( {2+\frac{3}{{x-2}}} \right)}}dx=\int{{2dx+\int{{\frac{3}{{x-2}}}}}}dx=2\int{{1dx+3\int{{\frac{1}{{x-2}}}}}}dx=2x+3ln |x-2|+C
Wynik drugiej całki otrzymałam licząc przez podstawienie.
\displaystyle \int{{\frac{1}{{x-2}}}}dx=| {\begin{matrix} t=x-2 \ dt=dx \end{matrix}} |=\int{{\frac{1}{t}}}dt=ln |t|+C=ln |x-2|+C
Mam całkę 1/dx, ale w kalkulator nie można wpisać dx, więc jest problem……
Coś nie tak z tą całką nie halo, dx nie powinno być w mianowniku…
Witam. Czy w lekcji 4 o całkach nieoznaczonych (części + podstawienie) gdy jest całka z x cos^2x za u bierze Pan cos^2x a za v’x, można podstawić odwrotnie? Tzn u=x a v’=cos^2x ?
Można.
Witam
Mam problem z taką całką: \integral (x^2)*(1+x^2)^(1/2) dx
Czy mogę prosić Pana o jakąś “drobną” wskazówkę?
Pozdrawiam
witam mam problem z policzeniem całki z kursu całek nieoznaczonych z lekcji 4 (zadanie domowe nr 15). Proszę o pomoc
Mamy do obliczenia całkę
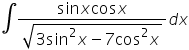
Najpierw skorzystamy ze wzoru:
GENIUSZ!!!
Pomocy! mam do obliczenia nastepujaca calke: (x^0.5)*((r^2-(H-x)^2)^0.5) gdzie r i H to stale, kalkulator tego niestety nie liczy… ;(
Stary, jesteś moim zdaniem PROMETEUSZEM 21 wieku, 2 dni do egzaminu, ale dzięki kursowi z całek nieoznaczonych myślę że, dam rady.
Ja przez noc ogarnąłem 😉 MISZCZ xD
t=cosx =) Pozdrawiam
Witam Panie Krystianie!
Mam problem z całka cos^7xsinxdx jak to policzyć ?
Rozumiem że za t=cos^7x co daje nam pochodna -7cos^6sinx , dalej nie rozumiem jak to ustrojstwo policzyć.
Proszę o pomoc
\displaystyle \int cos^7xsinxdx = -cos^8x-7 \int cos^7xsinx =
-\frac{cos^8x}{8} + C
\displaystyle f(x)=cos^7x
\displaystyle g'(x)=sinx
Akurat to jest bardzo latwa calka. Pan
Krystian dobrze omawia korzystanie z tej metody w swoim
kursie:).
Dzięki!
Nie ma sprawy.
Witam. Mam problem z całką nr 3 z zadania domowego z kursu całek nieoznaczonych (lekcja 5 – całki wymierne). Nie mogę się połapać w którym miejscu robię błąd bo wynik wychodzi mi taki: 0,75 ln|x+0,75| + 0,25 ln|x-0,25|+C.
Witam. No to w odpowiedziach jest tak samo: \frac{1}{4}ln \left| x-\frac{1}{4} \right|+\frac{3}{4}ln \left| x+\frac{3}{4} \right|+C…?
Zasadniczo to 0.75 to nie jest 1/4 jak coś a 0.25 to nie 3/4
Zasadniczo dodawanie może być przestawne najpierw jest 0.25 czyli 1/4 a potem 0.75 czyli 3/4
Hahaha, zasadniczo miałem to samo napisać, że dodawanie jest przemienne 😀
Proszę o pomoc przy obliczeniu całki \int_{2}^{4}\frac{1}{x-1}*sqrt{1+\frac{1}{(x-1)^4}}dx
Dzięki. Na pewno skorzystam z kalkulatora. Właśnie szukałem czegoś podobnego. Pomocna strona.