这篇文章是第三篇,我想让你注意一下在大学数学学习开始时值得复习的事情。快速复习这些会让你的大学生活轻松很多。在之前的文章中,我讨论了以下主题:
今天轮到二次函数。
二次函数?但是我们好像做了两个月…
二次函数的主题当然非常广泛,我的意思并不是要你拿起高中的课本,从头到尾把整个章节都过一遍。
我们只关注一些重要的细节,细微之处和陷阱。
二次函数与二次方程
二次函数当然是这样的东西:
![]() 或者:
或者: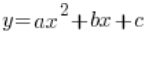
其中 ![]() 是任意数。二次函数的例子是:
是任意数。二次函数的例子是:
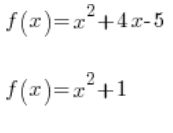
等等…
二次函数的概念应该与二次方程的概念区分开,例如:
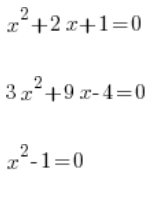
等等…
这不是同一回事!!!
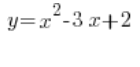 是二次函数,而
是二次函数,而 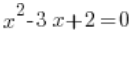 是二次方程。
是二次方程。
在大学里经常会因为无法区分函数和方程而出现…
严重错误一
计算例如导数并给出一个函数时:
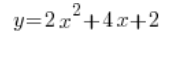
人们经常会做这样的事情:
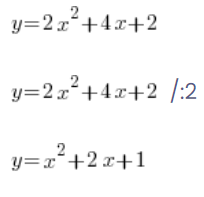
…然后继续计算所需的内容。
他们这样做是因为记得可以在方程中这样做:
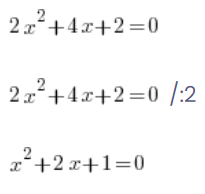
…在方程中一切正常,可以对两边同时除以 2,右边的 0 除以 2 确实为 0,方程是等价的(有相同的解)。
但是,这个操作不能在函数上进行——必须至少对左边的 y 进行除法等等。仅仅将函数值除以 2 会得到一个不同的函数!
需要复习的函数知识?
并不多。实际上只有两种形式的函数:标准形式和乘积形式。
二次函数的标准形式
我假设我们已经有了二次函数的通用形式:
![]()
它的标准形式是:
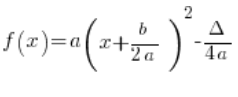
即:
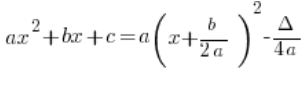
什么是 a,b 和 ![]() 这是众所周知的,几乎没有人对此有问题,
这是众所周知的,几乎没有人对此有问题,![]() 也一样。
也一样。
我们甚至可以注意到,如果我们在标准形式中将 ![]() 提出来,我们会得到:
提出来,我们会得到:
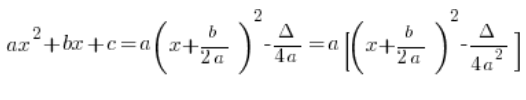
…有时可能有用,有时则不然。
如果你学过这个,通过计算顶点坐标(通常是 ![]() 和
和 ![]() )并代入公式:
)并代入公式:
![]() 这当然有点绕道,但也不错。
这当然有点绕道,但也不错。
记住 ![]() 在标准形式公式的开头!
在标准形式公式的开头!
二次函数的乘积形式(将其分解为因子):
现在回到我们的通用二次函数:
![]()
我们常常需要“将其分解为因子”,使用二次函数的乘积形式:
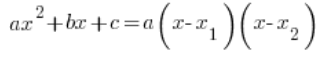
其中 ![]() 和
和 ![]() 我们使用已知和喜欢的公式计算:
我们使用已知和喜欢的公式计算:
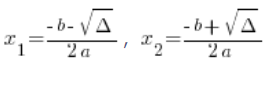
在这里你也必须记住 ![]() 在公式的开头!!!
在公式的开头!!!
还要注意,这些 ![]() 和
和 ![]() 并不总是存在(如果 Δ 是负的,则不存在),这意味着函数并不总是可以写成乘积形式,即二次函数并不总是可以分解为因子。
并不总是存在(如果 Δ 是负的,则不存在),这意味着函数并不总是可以写成乘积形式,即二次函数并不总是可以分解为因子。
需要复习的二次方程知识?
关于二次方程,我猜情况不是很糟。我们通常可以解决一般方程:
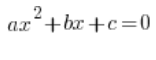
例如:
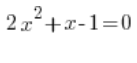
我们只需要计算:
![]()
然后,如果 Δ 是非负的,解方程:
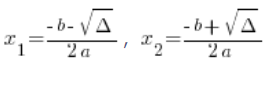
记住,在分母中有 ![]() 而不仅仅是 2!
而不仅仅是 2!
我想停下来讲一下特定的方程:
![]()
这里会发生很多错误。例如:
严重错误二
![]()
![]()
究竟是什么错误?数字 2 确实是方程 ![]() 的解,但完全忽略了这个方程的第二个解,即数字 -2。应该是:
的解,但完全忽略了这个方程的第二个解,即数字 -2。应该是:
![]()
![]()
在几何中可以忽略负解(因为距离不能为负)。
方程形式的另一个问题:![]() 是:
是:
严重错误三
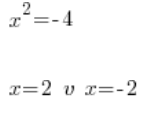
这当然是胡说八道,因为 2 的平方不是 -4。实际上,没有什么平方会得到 -4(那些已经学过复数的同学请保持安静)。方程:
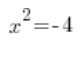
…没有任何解。
所以要保持警觉。方程 ![]() 有两个解,而方程
有两个解,而方程 ![]() 根本没有解。
根本没有解。
我邀请大家冷静地复习到目前为止所说的所有内容,当然也欢迎在评论中提问。


