计量经济学 讲座 1
主题:什么是计量经济学?
许多人问过我:
计量经济学——这到底是什么?
尤其是当他们听说我学的是“信息学与计量经济学”时(是的,没错,确实有这样的专业 🙂)。这个名字确实挺神秘的。但事实上,计量经济学本身的内容也很有意思。甚至可以说,它与生活息息相关——也就是说,我们在这里学到的东西,真的可以在现实生活中用得上。
那开始学习计量经济学需要什么呢?
一个能做简单计算的计算器、一些关于各种函数的基本知识、一定的想象力以及联系事实的能力。剩下的自然会慢慢掌握。
我们先来看一个简单的例子。
例 1
在一组随机抽取的学生中,我们询问他们在一次重要的小测验前花了多少时间学习(以小时为单位)。然后检查他们得到的成绩。结果如下表所示:
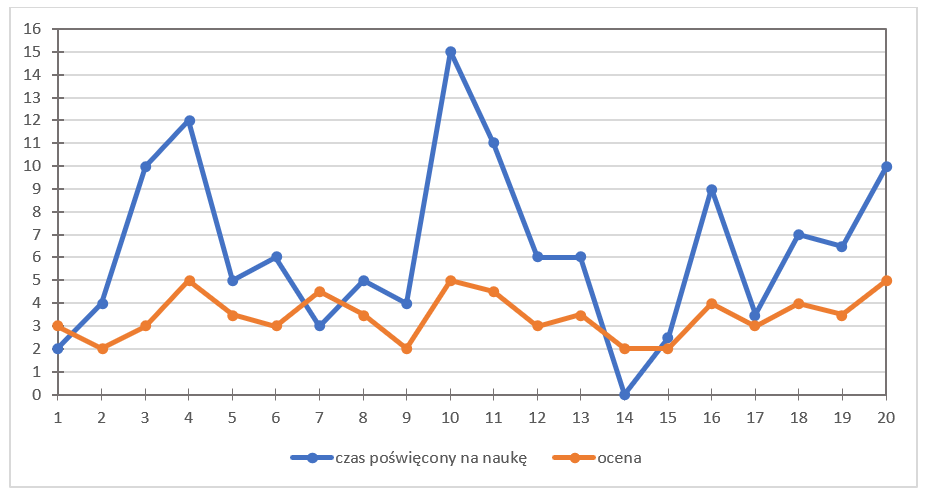
嗯……光看这些数字,很多人可能什么也看不出来。因此,值得先为每个变量单独画出图表,也就是说,对每个学生标出他们的成绩值和学习时间。
如下所示:
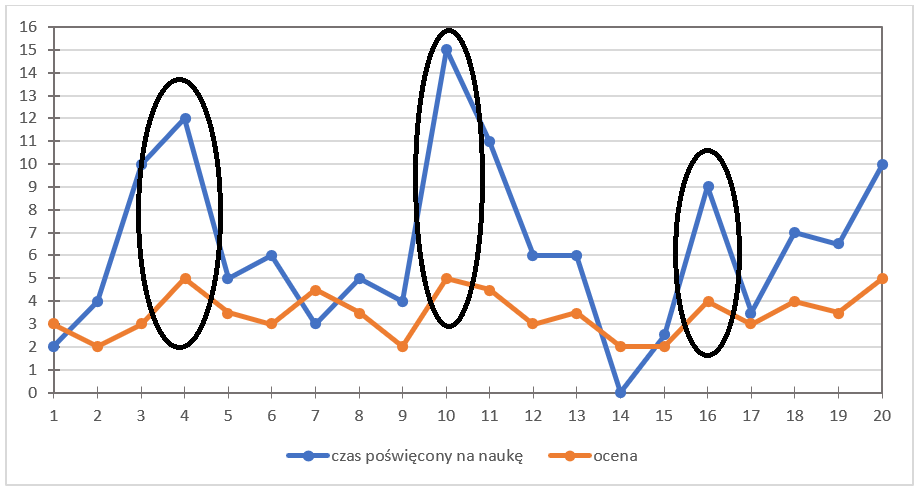
为什么图上会有这样的“波浪”?X 轴表示学生编号,Y 轴表示成绩值(橙色线)以及学习时间(蓝色线)。正确地标出这些点非常重要,因此请仔细观察表格和图上的点。
我特意把这两个变量放在同一个图上。为什么呢?为了让我们能够直观地观察这两个变量之间的关系——不是相对于学生编号,而是彼此之间。也许学习时间和成绩之间存在某种关系?
你一定注意到,这两条线都有“高峰”和“低谷”。这些峰谷是否在同一个学生那里同时出现呢?
没错,可以明显看出确实如此。例如,这里是一些高峰:
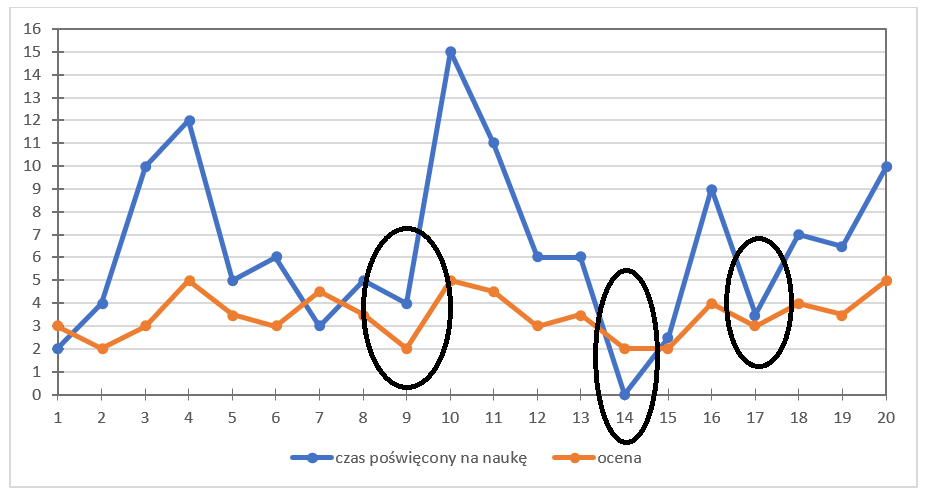
而这里是低谷:
可以看到,当我们分析反映某个具体现象的数据时(确实,对某些人来说,考试前学习可以算是一种“现象” 😄),往往能发现某些关联。你怎么看?
没错,从图中可以明显看出:学习时间越长,成绩越高(反之亦然)。通常这是正确的,甚至非常正确。当然,每个规律都有例外。(这让我想起一句话:学得像 2 分,想着能得 3 分,结果得了 4 分,还在想为什么不是 5 分 😄。)
既然我们已经得出了这两个变量之间存在某种关系的结论,那就让我们试着为这些数据画出另一张图——这次我们让学习时间依赖于成绩。也就是说,在坐标系中标出的点不再是“学生编号”和某个特征的配对,而仅仅是这两个特征本身:
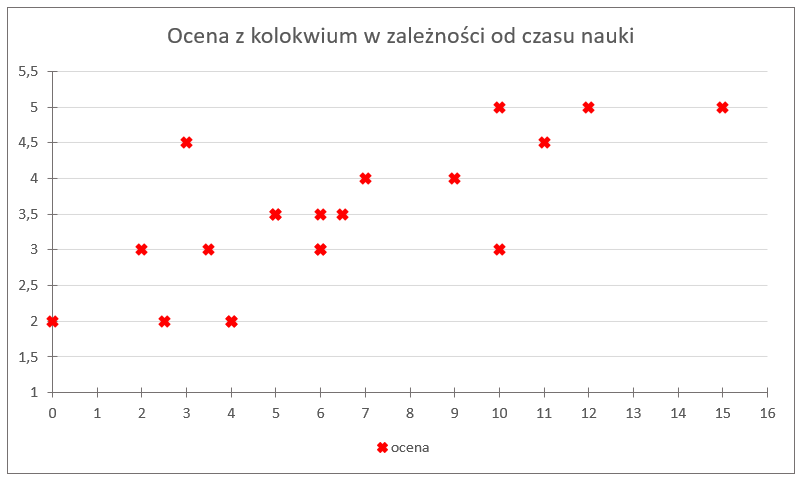
我们把学习时间定义为变量 X,而成绩定义为变量 Y。于是可以得到如下标出的点:
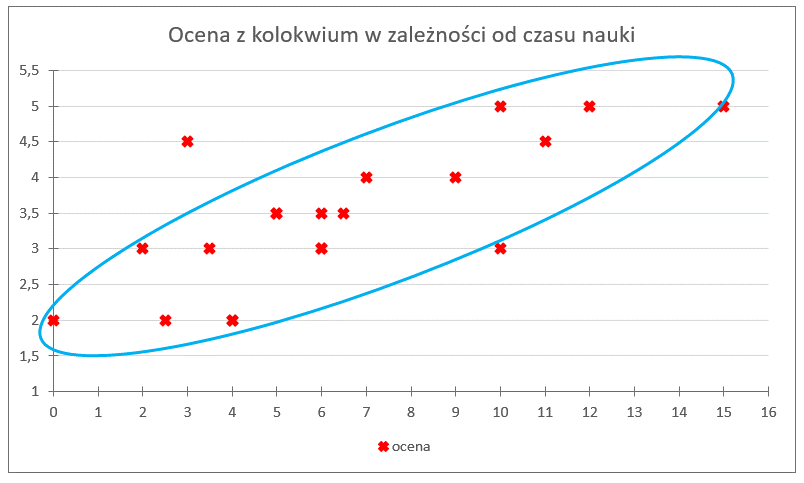
可以看到,这些点没法被一条折线顺利连接起来——根本不行。但这团“点云”却呈现出一种有规律的形状,来看一下:
你觉得这种形状如何?它的倾斜方向说明了什么?
可以看到,这些点大致呈“细长的上升形态”。这说明我们之前发现的关系——“学习时间越长,成绩越高”——得到了验证。至于形状,可以更进一步地说,它接近于一条直线,也就是说,它近似线性关系:可以用一条上升的直线去“包住”这团点。
结果表明,这两个特征之间的规律可以用数学形式表达出来。是不是很神奇?
当然要记住,这并不是一种精确的描述,而是一种近似的数学函数,它尽可能地拟合并反映这种关系。在这里,它表现得像一条直线——即线性函数。
既然我们确定可以用一个函数去“涵盖”大多数点,那么这就意味着这种关系是可以度量的。接下来只需要找出如何构建、计算这个函数,并理解它能帮我们做什么。
这时候,计量经济学就派上用场了!
计量经济学的概念
在 20 世纪初,一位波兰学者将两个希腊词组合在一起:oikonomia(意为“管理、经济”)和 metron(意为“度量”),创造出了一个新词——计量经济学(Econometrics)。从字面意义上讲,就是“对经济进行度量”。
听起来确实很有道理 😊 因为这正是计量经济学的核心思想——用数学和统计方法去“度量”经济现象中存在的规律。它的目标就是解释一个变量的变化如何取决于其他变量的变化。
因此,在计量经济学中,起作用的不仅仅是数学,还有统计学。数据不能凭空想象出来,而应尽量基于真实的资料。这样的数据,我们称之为统计数据。所以,计量经济学其实可以看作是统计学的“自然之子”。
回到我们的例子。我们已经观察到现实生活中的一些变量之间存在某种关系,因此可以大胆地说,在经济变量之间也存在类似的关系。
假设现在有另一位学生——第 21 号同学,他根据前面同学的数据分析,想大致“计算”一下:为了得到理想的成绩(比如 3 或 3.5 就够了),需要学习多长时间?或者反过来说,如果他学习半天,可以期望得到什么样的成绩?
要回答这些问题,也就是要进行某种“计算”,我们需要一个具体的方程式。于是这里引出了一个新的概念——计量经济模型。
计量经济模型的概念
计量经济学分析中最基本的工具就是计量经济模型。模型(这里可不是时装模特 😄)是一种用于分析的理论性数学结构,它替代现实中的复杂现象,帮助我们更好地理解其本质。通过一个或多个方程,它描述我们选定的经济变量之间的相互关系。换句话说,它是一个经过统计方法“拟合”到现实的数学模型。
要注意的是,模型始终是对现实的一种简化。就像飞机模型或 DNA 双螺旋模型一样,它以形象的方式呈现现实中存在的事物。计量经济模型同样如此——它只考虑最重要的因素,忽略次要的部分。毕竟,我们不可能把所有可能性都考虑进去,对吧?🙂
模型通常用方程来表示。它的一般形式如下:
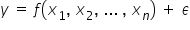
这样的模型包含几个固定组成部分:
首先是变量 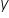 ——这是我们希望通过模型来解释的变量,因此称为被解释变量或因变量。
——这是我们希望通过模型来解释的变量,因此称为被解释变量或因变量。
变量 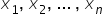 表示接下来的 n 个自变量(也称“解释变量”)。它们用于解释因变量的变化。有时候只需要一个解释变量就足够了。每个解释变量都应具有明确的经济含义。
表示接下来的 n 个自变量(也称“解释变量”)。它们用于解释因变量的变化。有时候只需要一个解释变量就足够了。每个解释变量都应具有明确的经济含义。
函数 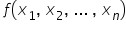 表示因变量与解释变量之间的函数关系,其中还包含一个随机成分。
表示因变量与解释变量之间的函数关系,其中还包含一个随机成分。
说到这里,我们就遇到了这个神秘的符号 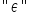 ——这其实是希腊字母 ε (epsilon),表示所谓的随机误差项。简单说两句关于它的意义:
——这其实是希腊字母 ε (epsilon),表示所谓的随机误差项。简单说两句关于它的意义:
随机误差项代表模型中由于其他因素而产生的“扰动”。数学方程总是对现实的一种近似,因此误差项考虑了多种因素,例如:模型与现实之间的差异、未包含在模型中的其他变量的影响、测量误差,以及各种随机或意外因素的作用。
呼~理论部分到这里够多了 😄
回到我们的例子。我们已经确定,这两个特征之间的关系是线性的。现在可以用初中学过的知识回忆一下——线性函数的公式是什么样的?
对,就是这样: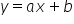 。
。
这里,变量之间通过加法和乘以常数(称为参数 (a, b))联系在一起。
那么,这就是我们的模型了吗?
答案是——差不多是这样 🙂
写下的这个方程表示的是一个理论模型。为了在符号上区分它与一般模型,人们通常会在 y 上加一个小帽子。于是方程
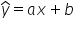
就可以视为一个理论性的计量经济学模型。
看来我们做得不错吧 😊
那如果我们想把它写得更一般一些——也就是考虑到所有可能的因素,包括那些被忽略或次要的变量——方程就会是这样的:
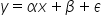
这是只有一个解释变量的情况。而如果我们有多个解释变量,则模型的形式如下:
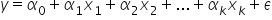
在正式的计量经济学写法中,人们通常使用希腊字母(如 α、β 等)来表示参数,这些参数稍后会通过数据计算出具体的数值。
在我们的例子中,我们研究的是学生考试成绩与学习时间之间的关系。但也许有人会问:是否可以反过来——学习时间依赖于考试成绩?那么我们就可以写出两种可能的模型:
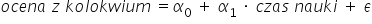
或是这样:
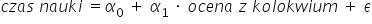
这时候,我们需要用到常识和对因果关系的理解。显然,第二个模型是不合理的——因为没人会在拿到成绩之后再去“测量”自己为那场考试花了多少时间学习,对吧?😄
因此,一般形式的模型应为:
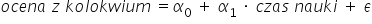
那这个符号 ε (epsilon) 到底代表什么呢?🤔
其他未被纳入模型的变量,例如:到课次数、授课教师当天的状态等。此外还存在一些隐藏的随机因素,比如学生突然生病——即使学了很多,因为身体虚弱、注意力下降而得到更低的分数。
此时,计量经济学的任务就是恰当地估计 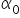 和
和 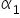 的取值。得到的数值为参数的估计量,通常记作
的取值。得到的数值为参数的估计量,通常记作 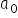 与
与 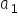 ,或有人更习惯写成
,或有人更习惯写成 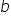 与
与 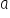 。例如:
。例如:
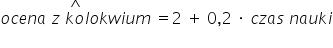
至于这些数值该如何计算,那就是另一个话题了 🙂
估计方法有很多,每种都有其适用前提。在这个具体模型里,我们假定了线性关系——它在验证和应用上都是最简单的。
当然,用来描述解释变量之间联系的函数 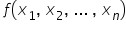 可以是任意形式(指数、对数、有理函数等,甚至是多种形式的组合)。接下来我们只需检验模型是否良好(是否满足相应假设),并据此得出一些结论与应用,例如为第 21 号同学计算他期望的取值。
可以是任意形式(指数、对数、有理函数等,甚至是多种形式的组合)。接下来我们只需检验模型是否良好(是否满足相应假设),并据此得出一些结论与应用,例如为第 21 号同学计算他期望的取值。
由此可见,计量经济学并不枯燥。确实,计算会不少——各种数字、公式、步骤(统计学里一向如此)。但只要你认真思考要解释的现象,选择合适的解释变量(不必拘泥于只有一个,多选一些也可以 🙂),你就能实际地刻画变量之间的关系(强度、方向),并据此“预测”出新的数值。
这些结果可能会让你惊喜!😊
结束