No products in the cart.
Krystian Karczyński- 29 4 月 2024
- Komentarz 0
带有 e 的数列极限……真的吗？
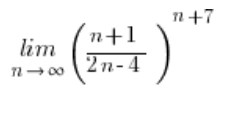
如果我们已经解决了一些数列极限的问题，我们可能会陷入一种惯性。并且开始像计算带有 e 的数列极限那样计算上面的极限，例如在分子里减去和加上 4，然后分成两个分数等。然而这样计算会导致一个小问题…
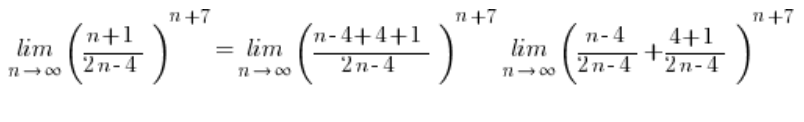
这次第一个分数根本没有简化，也没有得到一！
老师们通常不会对此详细讲解，但我们只有在出现未定型 
时才用到带有 e 的数列极限，在我们的例子中：
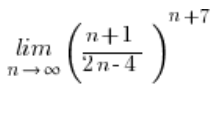
第二部分：
多项式的商被提高到一定的幂并不一定趋向于1，而是趋向于 
，通过将其中的最大次方提取到括号外可以看到：
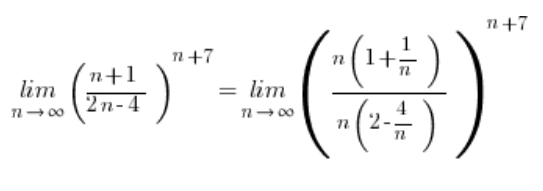
因此，我们有了情况 
，这种情况下的数列极限等于零：
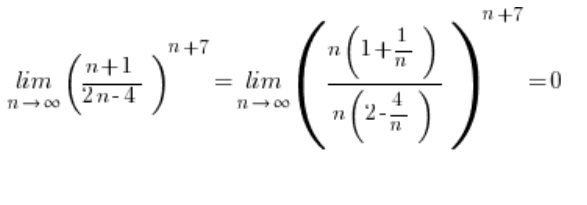
这类极限的问题
在你使用涉及 e 数的公式来解决数列的极限之前，值得考虑一下这个被提高到一定幂的表达式是否会趋向于1。对于多项式除法，可以轻松检查，无需计算。如果多项式的最大次方相同，并且它们的系数也相同，则这个除法会趋向于1。在这种情况下，您可以使用涉及 e 数的公式。如果不是这种情况，很可能需要将最大的次方提取到括号外。
你自己估计一下
最后是练习。看看下面的极限，用“肉眼”判断哪些应该用 e 数的公式来解决，哪些应该用提取最大次方的方法：
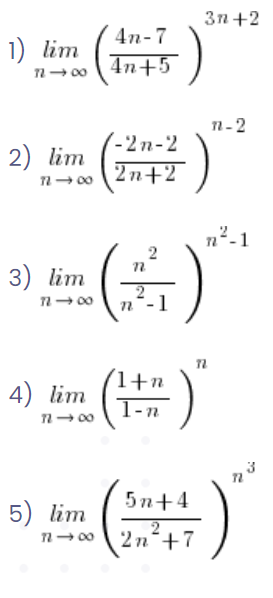
…它们看起来如此相似… 🙂
