No products in the cart.
Krystian Karczyński- 2 7 月 2024
- Komentarz 0
在解决复数问题时，要记住复数的三角形式如下：
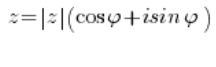
就这样。不多也不少。
所以，我们要注意：
什么时候复数是三角形式，什么时候不是？
- 数： 是三角形式的复数，其中复数的模等于1 ()，因为显然：
- 数： 不是三角形式的复数，因为在与’i’相乘的正弦前有一个负号，而应该是正号。
要将这个数转换为三角形式，需要使用三角公式：
使用这些公式，我们可以转换：
正弦和余弦函数是-周期的，因此它们的值与 相同。关于这个话题，我在这篇文章中写了更多内容。
最后我们得到：
…这就是三角形式的复数。 - 数： 不是三角形式的复数，因为在与’i’相乘的正弦前有一个负号，而应该是正号，并且在余弦前有一个负号，而应该是正号。
要将这个复数转换为三角形式，需要在括号前加一个负号：
将数 转换为三角形式（我们已经会了…）：
所以我们有两个三角形式的数相乘：
要相乘三角形式的数，需要相乘它们的模并相加它们的参数（有公式），所以我们得到：
这就是三角形式的数。 - 数： 不是三角形式的复数，因为在余弦前有一个负号，而应该是正号。
要将这个复数转换为三角形式，需要把负号提到括号前：
我们需要将 -1 转换为三角形式（我们在第3点中做过），同样，我们需要将 转换为三角形式（我们在第2点中做过）。
我们会得到：
使用三角函数的乘法公式：
并利用 的周期性：
- 数： 不是三角形式的复数，因为在余弦前有一个虚数单位 ‘i’（不应该在那里），而在正弦前没有虚数单位 ‘i’。
需要使用高中学习过的三角公式：
我们有：
这就是三角形式的复数。 - 数： 不是三角形式的复数。
需要将正弦和余弦互换，就像在第5点中做的那样，然后像在第4点中一样求解。 - 数： 不是三角形式的复数。
需要将正弦和余弦互换，就像在第5点中做的那样，然后像在第2点中一样求解。 - 数： 不是三角形式的复数。
需要将正弦和余弦互换，就像在第5点中做的那样，然后像在第3点中一样求解。
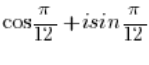是三角形式的复数，其中复数的模等于1 (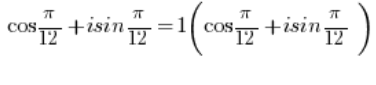
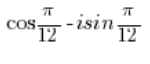)，因为显然：
不是三角形式的复数，因为在与’i’相乘的正弦前有一个负号，而应该是正号。
-周期的，因此它们的值与 
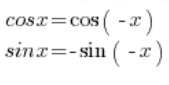
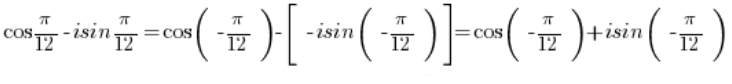
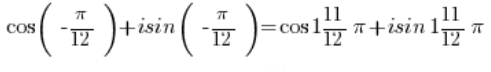
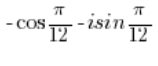不是三角形式的复数，因为在与’i’相乘的正弦前有一个负号，而应该是正号，并且在余弦前有一个负号，而应该是正号。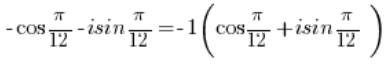
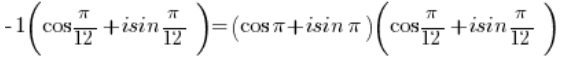
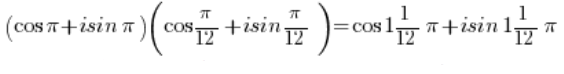
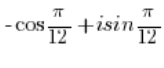转换为三角形式（我们已经会了…）：
不是三角形式的复数，因为在余弦前有一个负号，而应该是正号。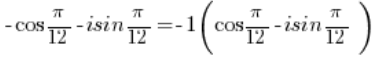
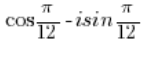转换为三角形式（我们在第2点中做过）。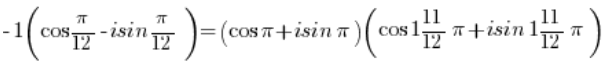
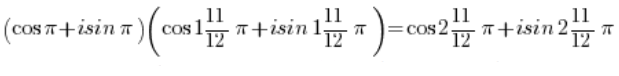
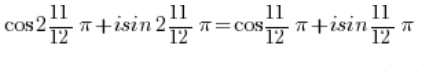
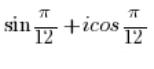不是三角形式的复数，因为在余弦前有一个虚数单位 ‘i’（不应该在那里），而在正弦前没有虚数单位 ‘i’。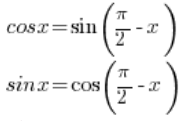
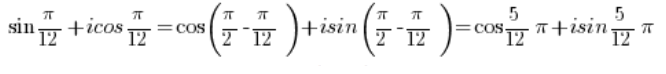
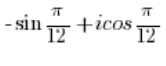不是三角形式的复数。
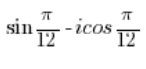不是三角形式的复数。
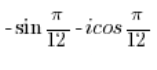不是三角形式的复数。祝你好运！ 🙂
