将某些四次方程简化为二次方程
许多四次多项式方程可以用这里描述的高中常见技巧简化为二次方程：
当然，这对于复数多项式也是有效的。
提醒一下，我们说的是 拥有方程：
{{z}^{4}}+3{{z}^{2}}+2=0我们代入： {{z}^{2}}=t
得到二次方程：
{{t}^{2}}+3{t}+2=0然后用普通的 delta 来解决，等等，我们得到解 
，记住 
我们从中形成两个新的方程：
或 
解决它们，我们有四个解：
。
将某些高次方程简化为二次方程
完全没有什么阻碍，将这种方法扩展到高于 4 次的方程（当然，如果它们能通过代入简化为二次方程）。
所以有：
2{{z}^{6}}-5{{z}^{3}}+4=0也可以注意到它等价于：
2{( {z}^{3})^{2}}-5{{z}^{3}}+4=0并代入： 
我们得到二次方程：
2{{t}^{2}}-5t+4=0在方程：
{{x}^{10}}-3{{x}^{5}}+1=0代入后：
我们得到：
{{t}^{2}}-3t+1=0等等，等等…
示例
我们来看这个方程：
z^6+(1-i)z^3-i=0我们代入 z^2=t 然后有：
t^2+(1-i)t-i=0继续计算：
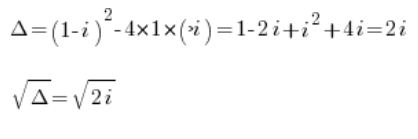
我们用复数的方法计算这些根（例如在我的 课程 中展示的）。
我们有 
或 
即：
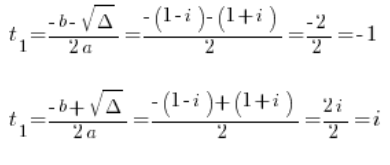
记住这还不是解，因为 z^3=t
所以我们需要解决的方程是：
z^3=-1以及：
z^3=i我们将其转化为：
以及 
并使用已知的方法计算，我们从第一个方程得到三个根：
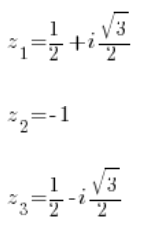
以及从第二个方程得到三个根：
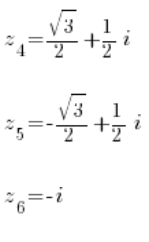
解决了 🙂
Related Posts
函数极限计算器（已过时） + 新计算器
Posted on
证明当 x 趋向于无穷大时 sin(x) 不达到极限
Posted on