Currently Empty: zł0.00

具有e值公式的典型序列极限
传统的具有e值公式的序列极限问题通常会“自然地”导致公式(在我的课程中,我展示了如何做到这一点):
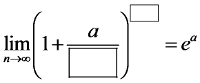 但是,如果括号里没有这样一个优美的分数,而是像这样的东西:
但是,如果括号里没有这样一个优美的分数,而是像这样的东西:
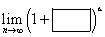 如果括号内的矩形趋近于零,而指数中的三角形趋近于无穷大,我们实际上有一个不定式符号
如果括号内的矩形趋近于零,而指数中的三角形趋近于无穷大,我们实际上有一个不定式符号![]() – 正是我们使用e值公式的情况。怎么办?
– 正是我们使用e值公式的情况。怎么办?
嗯,记住,任何表达式都可以表示为1除以该表达式的倒数 🙂
例如,普通的数字2可以表示为:
![]()
所以,如果真的需要,任何表达式都可以“强制”变成一个分数。
具有e值公式的非典型极限示例
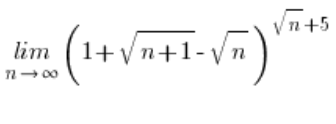
首先,需要证明表达式![]() 趋近于零。你可以通过计算极限来做到这一点:
趋近于零。你可以通过计算极限来做到这一点:
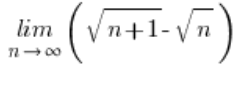 – 结果确实为零(可以使用共轭相乘法)。
– 结果确实为零(可以使用共轭相乘法)。
现在,替换:
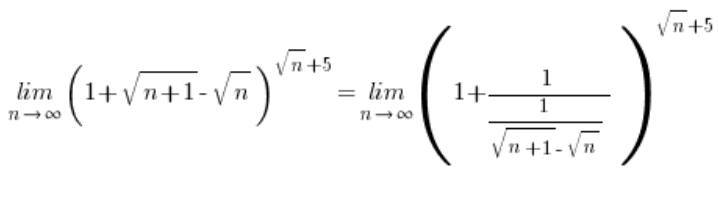
…然后按照已知步骤继续:
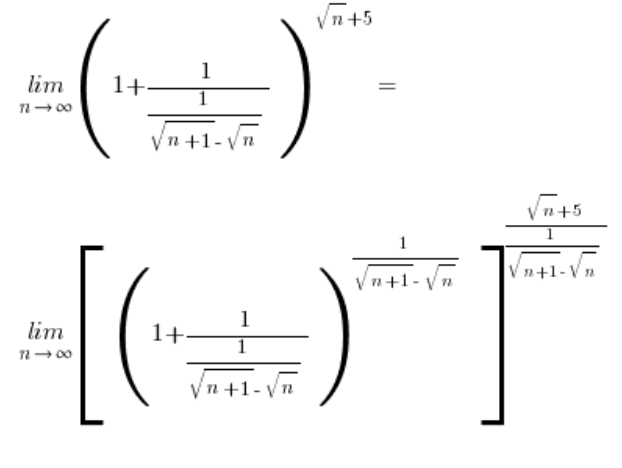
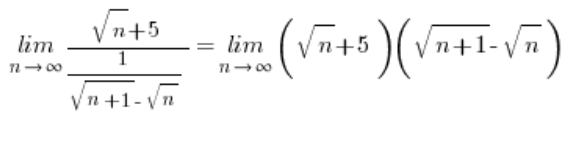
…通过应用共轭相乘法,得到结果![]() 。
。
因此,整个极限为:
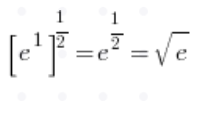

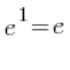 – 根据基本公式
– 根据基本公式