Rząd macierzy Wykład 1
Temat: Rząd macierzy – definicja
Streszczenie
W artykule przedstawię po prostu, co to jest rząd macierzy.
Wstęp – definicja wektora
Zanim przejdziemy sobie do samego pojęcia macierzy, powiemy sobie, czym jest wektor. Z wektorami spotkaliśmy się już w szkole średniej i być może na studiach przy okazji geometrii analitycznej. Tam oznaczały one przesunięcie na płaszczyźnie, np. [2,-4] – był to wektor oznaczający przesunięcie na osi OX o dwie jednostki w prawo, a na osi OY o cztery jednostki w dół. Wektory oznaczało się strzałkami. [3,-2,5] – był to wektor w przestrzeni trójwymiarowej, a jego współrzędne oznaczają przesunięcia po odpowiednich osiach. Również i jego można wyobrazić sobie jako strzałkę.
Rozszerzając jednak pojęcie wektora na więcej współrzędnych otrzymamy macierz jednowierszową, np. [3,0,-1,4,5,10,-2,4,4] – jest to wektor 9-wymiarowy. Nie musi on oznaczać jakiegokolwiek geometrycznego przesunięcia (ruch w 9 wymiarach? – hmmm…), ale na przykład ceny w koszyku inflacyjnym, czy coś takiego.
Zapomnijmy więc o wektorach jako przesunięciach geometrycznych i umówmy się na nową definicję: wektor to macierz jednowierszowa (albo jednokolumnowa – to wszystko jedno).
Definicja wektorów zależnych i niezależnych
Jak już wiemy, co to jest wektor, możemy określić sobie, kiedy dwa (na początku) wektory są od siebie liniowo zależne. Dwa wektory \vec{x}, \vec{y} nazwiemy liniowo zależnymi, gdy istnieje taka liczba, że po przemnożeniu przez tą liczbę jednego z wektorów są one równe, tzn.
\underset{k}{\exists} \vec{x} =k\cdot\vec{y}Gdzie symbolem \vec{x} oznaczamy wektor, a ten dziwny symbol: \exists to odwrócona literka „e” od angielskiego „exists”, czyli „istnieje”. \underset{k}{\exists} czytamy więc: „istnieje k”.
Przykłady dwóch wektorów zależnych to:
Przykład
\vec{x}=[1,3,5] i \vec{y}=[2,6,10] są liniowo zależne, bo wektor \vec{y} to wektor \vec{x} przemnożony przez 2.
Geometryczną interpretacją zależności liniowej dwóch wektorów dwu albo trzy wymiarowych jest ich kierunek, tzn. wektory zależne liniowo mają ten sam kierunek, a różnią się tylko zwrotem lub długością.
Oczywiście nie ma mowy, żeby na przykład wektory: \vec{x}=[1,2,0,4] i \vec{y}=[-1,-4,0], czyli wektory mające różne wymiary (różną liczbę elementów) były liniowo zależne. Nie znajdziemy przecież takiej stałej, co po przemnożeniu zmienia wymiar macierzy, prawda?
Liniową zależność wektorów można określać jednak dla większej ich liczby. Definiujemy ją wtedy następująco:
Definicja
Wektory \vec{x_1},\vec{x_2},\vec{x_3},...,\vec{x_n} nazywamy wektorami liniowo zależnymi, jeżeli istnieją takie stałe {\alpha}_1,{\alpha}_2,{\alpha}_3,...,{\alpha}_n (z których co najmniej jedna jest różna od zera), że:
{\alpha}_1\vec{x_1}+{\alpha}_2\vec{x_2}+{\alpha}_3\vec{x_3}+...+{{\alpha}_n}\vec{x_n}=\vec{0}Na odwrót powiedzielibyśmy, że dwa wektory są liniowo niezależne, jeżeli NIE istnieją takie stałe {\alpha}_1,{\alpha}_2,{\alpha}_3,...,{\alpha}_n (z których co najmniej jedna jest różna od zera), że:
{\alpha}_1\vec{x_1}+{\alpha}_2\vec{x_2}+{\alpha}_3\vec{x_3}+...+{{\alpha}_n}\vec{x_n}=\vec{0}Geometryczną interpretacją liniowej zależności wektorów trzywymiarowych jest ich „komplanarność”, tzn. należenie do jednej płaszczyźnie. Trójwymiarowe wektory liniowo zależne są komplanarne, tzn. leżą na jednej płaszczyźnie.
Obliczanie liniowej niezależności wektorów
Nietrudno sobie wyobrazić, że zadanie polegające na określeniu tego, czy wektory są liniowo zależne, czy niezależne z definicji jest męczące (a nawet męczące z definicji). Na przykład dla wektorów czterowymiarowych:
\vec{x_1}=[1,3,-2,4] \vec{x_2}=[1,-1,3,5] \vec{x_3}=[0,1,4,-2] \vec{x_4}=[10,-2,5,1]Musielibyśmy sprawdzić, czy istnieją takie stałe {\alpha}_1,{\alpha}_2,{\alpha}_3,{\alpha}_4 (takie, że co najmniej jedna z nich różna jest od zera), że:
{\alpha}_1[1,3,-2,4]+{\alpha}_2[1,-1,3,5]+{\alpha}_3[0,1,4,-2]+{\alpha}_4[10,-2,5,1]=[0,0,0,0]Czyli (po przemnożeniu wektorów przez stałe):
[{\alpha}_1,3{\alpha}_1,-2{\alpha}_1,4{\alpha}_1]+[{\alpha}_2,-{\alpha}_2,3{\alpha}_2,5{\alpha}_2]+[0,{\alpha}_3,4{\alpha}_3,-2{\alpha}_3]+[10{\alpha}_4,-2{\alpha}_4,5{\alpha}_4,{\alpha}_4]=[0,0,0,0]Co jest równoważne układowi równań:
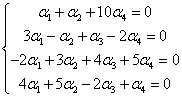
Teraz trzeba by sprawdzić, czy istnieją jakieś rozwiązania tego układu z wyjątkiem takiego, że wszystkie {\alpha}_1,{\alpha}_2,{\alpha}_3,{\alpha}_4 równe są zero.
Długie, żmudne, niewygodne, prawda?
Rząd macierzy
Tutaj dochodzimy właśnie do tego, czym jest rząd macierzy. Jeżeli wektory poukładamy wierszami (albo kolumnami – wszystko jedno) jeden pod drugim otrzymamy macierzy, prawda? Na przykład dla naszych wektorów z przykładu powyżej była by to:
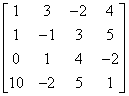
Zdefiniujmy rząd macierzy:
Definicja
Rząd macierzy to maksymalna liczba liniowo niezależnych wektorów będących wierszami (lub kolumnami) tej macierzy.
Obliczanie rzędu macierzy jest już o wiele, wiele łatwiejsze niż szarpanie z definicji (jak to dokładnie robić, przedstawione jest na przykład w moim Kursie Macierzy). Interpretacja wyniku jest prosta. Jeżeli rząd tej macierzy po obliczeniu równy był by 3, oznacza to, że w tych wektorach są tylko 3 liniowo niezależne od siebie, czyli ta czwórka jako całość jest liniowo zależna.
Tak się jednak składa, że:
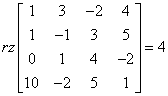
Czyli że rząd tej macierzy równy jest cztery. Mamy więc cztery wektory, spośród których 4 są liniowo niezależne. Oczywisty wniosek jest taki, że te wektory są liniowo niezależne.

Michał
Nie rozumiem, czemu w tym przypadku metoda zawiodła[ 2 -1 1 1] [1 2 -1 4][1 7 -4 11]mając taką macierz jej rząd jest równy 2. Licząc Pana sposobem doliczyłem się 3. Prosze czy ktos moze to sprawdzic bo ja juz nie rozumiem…
Macierz
Panie Krystianie, Pana metoda jest skuteczna, ale co zrobić w takiej macierzy: problem polega na tym, że w pewnym momencie nie ma jedynki w kolumnie i nie da się jej „zrobić”.
problem polega na tym, że w pewnym momencie nie ma jedynki w kolumnie i nie da się jej „zrobić”.
Cezary
W macierzy, o której Pan/Pani mówi w pewnym momencie dochodzimy do takiej sytuacji:2 + rz Teraz wystarczy od pierwszego wiersza odjąć wiersz trzeci,a to = 2 + rz
Teraz wystarczy od pierwszego wiersza odjąć wiersz trzeci,a to = 2 + rz  = 2 + rz
= 2 + rz  = 3Wyznacznik z tej macierzy = 0, więc rz = 3.
= 3Wyznacznik z tej macierzy = 0, więc rz = 3.
karola
Czy można obejrzeć filmik do tego kursu (liczenie rzędu macierzy)?
damiano444492
Przepraszam, że mój komentarz będzie nie w temacie.
Dotyczy wektorów, a to tematycznie blisko macierzy, nie miałem go gdzie indziej napisać.
Wydaje mi się, że w swoim pdfie „wektory bez układu”
https://etrapez.pl/wp-content/uploads/domowe/kga/wektorybukl.pdf
zrobił Pan błąd we wzorze na rzut wektora a na wektor b.
Dx
^
/
/
x—–>x——>x
A B C
„x” oznacza punkt.
Kąt CAD = kąt BAC = alfa
Na rysunku mamy trzy wektory:
1. Wektor a = wektor AD
2. Wektor b = wektor AC
3. Wektor a.b = wektor AB
Wektor a.b jest rzutem wektora a na kierunek wektora b.
Na rysunku nie jestem w stanie tego osiągnąć, ale punkt D zrzutowany pod kątem prostym na prostą AC da punkt B.
1.
Jak jest poprawnie?
widzimy, że wektor a.b obliczymy ze wozru (1*)
a.b = a * cos(alfa) (1*)
cos(alfa) weźmiemy z przekształcenia iloczynu skalarnego
a skalarnie b = |a|*|b|*cos(alfa)
stąd
a skalarnie b
cos(alfa) = —————
|a|*|b|
I ten wzór na cos(alfa) wstawiam do wzoru (1*)
a skalarnie b
a.b = a * —————
|a|*|b|
a a skalarnie b
a.b = — * —————
|a| |b|
I otrzymujemy wzór (1**)
a skalarnie b
a.b = i.a * ————— (1**)
|b|
gdzie i.a jest to wektor jednostkowy działający na kierunku wektora a (czyli równoległy do prostej AD)
2. A jak Pan zrobił?
W Pana pdfie wzór na rzut wektora a na wektor b wyraża się wzorem (2*)
a skalarnie b
a.b = b * —————- (2*)
(|b|)^2
Według mnie to jest błędny wzór, ponieważ
wykonując następujące przekształcenia
b a skalarnie b
a.b = —– * —————-
|b| |b|
dojdziemy do wzoru (2**)
a skalarnie b
a.b = i.b * —————- (2**)
|b|
gdzie i.b jest to wektor jednostkowy działający na kierunku wektora b (czyli równoległy do prostej AB)
No i teraz porównując wzory (1**) oraz (2**) widzimy, że różnią się jednym wyrazem:
we wzorze (1**) jest i.a
we wzorze (2**) jest i.b
Wiemy, że wektor i.a nie jest równy wektorowi i.b.
Więc jedna z tych opcji jest dobra (albo może być też tak, że żadna z tych dwóch opcji nie jest dobra – ale to według mnie nie ma miejsca)
I myślę, że to Pańska opcja jest tą niepoprawną.
Mógłby Pan podać wyprowadzenie, jak Pan do tego wzoru doszedł?
Być może, że się mylę albo nie rozumiem, w jaki sposób Pan mógł to wyprowadzić. Ale wydaje mi się, że Pańsk iwzór jest zły.
Beata
a ja znalazłam byka w zadaniu domowym. zadanie 1. przykład 3. rząd macierzy wychodzi 4. (w odpowiedziach że 3). wykluczyłam możliwość swojej pomyłki (sprawdzałam wielokrotnie; nie chce wyjść inaczej)
Beata
a nie sry; znalazłam literówkę; zwracam honor 😛
iza
a mi caly czas wychodzi 4. prosze o rozpisanie tego przykladu
Basia
Kurs macierze, lekcja 5 – rząd macierzy , minuta 20:30 . Mówi Pan, że rząd macierzy, której elementami są same zera jest równy zero. W takim razie rząd całej tej macierzy 5×5 nie powinien być 2, a nie 3?
Adam
Witam, znalazłem pewną nieścisłość w Pana Kursie Macierzy, lekcja 5 (Rząd macierzy) minuta 17:30, gdyby wybrać do 'wyzerowania’ wiersz pierwszy to byśmy otrzymali rząd macierzy:
-2 1 -3
-4 2 -2
-10 5 -15
z czego otrzymalibyśmy kolejny rząd macierzy
0 4
0 0
i koncowy wynik wyszedłby 4, a nie 3 tak jak na filmiku. Proszę, o odpowiedź bo nie wiem co teraz robić.
Krystian Karczyński
Prześledźmy to dokładnie. Mamy tam sytuację:
1+rz\left[ \begin{matrix}
1 & 0 & 1 & 4 \\
0 & 1 & 2 & 5 \\
1 & 2 & 5 & 14 \\
4 & 5 & 14 & 41 \end{matrix} \right]
Jeżeli chciał by Pan „wyzerować” pierwszy wiersz, przy pomocy jedynki z trzeciej kolumny (co jest jak najbardziej O.K.), trzeba trzecią kolumnę pomnożyć przez -1i dodać do pierwszej (to działania wykonał Pan poprawnie) i trzecią kolumnę pomnożyć przez -4i dodać do czwartej (a tu już są błędy).
Wyjdzie się więc na macierz:
1+rz\left[ \begin{matrix}
1 & 0 & 1 & 4 \\
0 & 1 & 2 & 5 \\
1 & 2 & 5 & 14 \\
4 & 5 & 14 & 41 \end{matrix} \right]=1+rz\left[ \begin{matrix}
0 & 0 & 1 & 0 \\
-2 & 1 & 2 & -3 \\
-4 & 2 & 5 & -6 \\
-10 & 5 & 14 & -15 \end{matrix} \right]=2+rz\left[ \begin{matrix}
-2 & 1 & -3 \\
-4 & 2 & -6 \\
-10 & 5 & -15 \end{matrix} \right]
W drugim wierszu trzeciej kolumny będzie -6, a nie -2.