Matrix rank Lecture 1
Topic: Matrix rank – definition
Summary
In the article, I will simply present what the rank of a matrix is.
Introduction – definition of a vector
Before we get to the matrix itself, let’s talk about what a vector is. We met with vectors in high school and perhaps in college, on the occasion of analytic geometry. There they meant a shift on the plane, e.g. [2,-4] – it was a vector representing a shift on the OX axis two units to the right, and on the OY axis four units down.
Vectors are indicated by arrows. [3,-2,5] – it is a vector in three-dimensional space, and its coordinates mean shifts along the appropriate axes. You can also imagine it as an arrow.
However, by extending the concept of a vector to more coordinates, we get a one-row matrix, e.g. [3,0,-1,4,5,10,-2,4,4] – it is a 9-dimensional vector. It doesn’t have to mean any geometric shift (movement in 9 dimensions? – well…), but, for example, prices in an inflation basket or something.
So let’s forget about vectors as geometric shifts, and let’s agree on a new definition : a vector is a single-row (or single-column, it doesn’t matter).
Definition of dependent and independent vectors
As we already know what a vector is, we can define when two (initially) vectors are linearly dependent on each other. We call two vectors \vec{x}, \vec{y} linearly dependent if there is a number such that when one of the vectors is multiplied by this number, they are equal, i.e.
\underset{k}{\exists} \vec{x} =k\cdot\vec{y}By the \vec{x} we denote a vector, and this strange symbol: \exists is an inverted letter “e” from the English ” exists “, meaning “exists”. \underset{k}{\exists} so we read: “there is k”. Examples of two dependent vectors are:
Example
\vec{x} =[1,3,5] and \vec{y}=[2,6,10] are lineart dependent, because vector \vec{y} is a vector \vec{x} multiplied by 2.
The geometrical interpretation of a linear relationship between two or three-dimensional vectors is their direction, i.e. linearly dependent vectors have the same direction and differ only in head/tail or length.
Of course, there’s no way that, for example, vectors: \vec{x}=[1,2,0,4] and \vec{y}=[-1,-4,0] , i.e. vectors with different dimensions (different number of elements) were linearly dependent.
After all, we can’t find a constant that changes the dimension of the matrix when multiplied, right?
However, the linear dependence of the vectors can be determined for a larger number of them. We then define it as follows:
Definition
Vectors \vec{x_1} ,\vec{x_2} ,\vec{x_3} ,...,\ vec{x_n} we call linearly dependent vectors if such constants exist {\alpha}_1,{\alpha} _2,{\alpha} _3,...,{\alpha} _n (of which at least one is non-zero) that:
{\alpha}_1\vec{x_1}+{\alpha}_2\vec{x_2}+{\alpha}_3\vec{x_3}+...+{{\alpha}_n}\vec{x_n}=\vec{0}Conversely, we would say that two vectors are linearly independent if there are NO such constants {\alpha}_1,{\alpha}_2,{\alpha}_3,...,{\alpha}_n (of which at least one is non-zero) that:
{\alpha}_1\vec{x_1}+{\alpha}_2\vec{x_2}+{\alpha}_3\vec{x_3}+...+{{\alpha}_n}\vec{x_n}=\vec{0}The geometrical interpretation of the linear relationship of three-dimensional vectors is their “coplanarity”, ie belonging to one plane. Three-dimensional linearly dependent vectors are coplanar, i.e. they lie in one plane.
Calculation of linear independence of vectors
It is not hard to imagine that the task of determining whether vectors are linearly dependent or independent by definition is tiresome (and even tiresome by definition). For example, for four-dimensional vectors:
\vec{x_1} =[1,3,-2,4]\vec{x_2} =[1,-1,3,5]\vec{x_3} =[0,1,4,-2]\vec{x_4} =[10,-2,5,1]We would have to check if such constants exist: {\alpha}_1,{\alpha}_2,{\alpha}_3,{\alpha}_4 (such that at least one of them is different from zero) that:
{\alpha}_1[1,3,-2,4]+{\alpha}_2[1,-1,3,5]+{\alpha}_3[0,1,4,-2]+{\alpha}_4[10,-2,5,1]=[0,0,0,0]That is (after multiplying vectors by constants):
[{\alpha}_1,3{\alpha}_1,-2{\alpha}_1,4{\alpha}_1]+[{\alpha}_2,-{\alpha}_2,3{\alpha}_2,5{\alpha}_2]+[0,{\alpha}_3,4{\alpha}_3,-2{\alpha}_3]+[10{\alpha}_4,-2{\alpha}_4,5{\alpha}_4,{\alpha}_4]=[0,0,0,0]Which is equivalent to the system of equations:
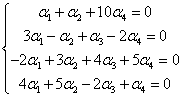
Now one would have to check if there are any solutions to this system except that all of them {\alpha}_1,{\alpha}_2,{\alpha}_3,{\alpha}_4 are equal to zero.
Long, tedious, inconvenient, right?
Matrix rank
This is where we come to exactly what the rank of a matrix is. If we arrange the vectors in rows (or columns – whatever) we get a matrix, right? For example, for our vectors from the example above, it would be:
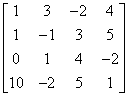
Let’s define the row of the matrix:
Definition
The rank of a matrix is the maximum number of linearly independent vectors that are rows (or columns) of that matrix.
Calculating the rank of a matrix is already much, much easier than fiddling with definitions (how to do it exactly is shown, for example, in my Matrix Course). The interpretation of the result is simple. If the rank of this matrix after calculations would be equal to 3, it means that in these vectors there are only 3 linearly independent of each other, so these four as a whole are linearly dependent.
However, it so happens that:
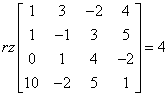
So the rank of this matrix is equal to four. So we have four vectors, 4 of which are linearly independent. The obvious conclusion is that these vectors are linearly independent .
Click to see how to use the row of a matrix to check if vectors form a basis (next Lecture) –>

