Całki Oznaczone Wykład 2
Temat: Całkowalność dowolnej funkcji ciągłej
Streszczenie
Na poprzednim Wykładzie zdefiniowałem całkę oznaczoną jako pewną sumę. Przypomnij sobie tą definicję i zastanów się, czy liczenie całek oznaczonych przy jej pomocy jest:
a) Łatwe
b) Trudne
Definicja całki oznaczonej
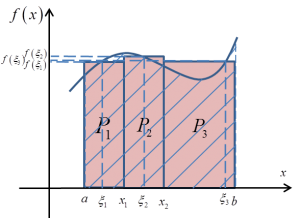
Obrazek powyżej dla przypomnienia, a definicja szła tak:
Mamy funkcje ciągłą ![]() określoną na przedziale
określoną na przedziale ![]() . Jej całką oznaczoną na tym przedziale nazywamy sumę:
. Jej całką oznaczoną na tym przedziale nazywamy sumę:
![]() ,
,
gdzie ![]() to długości przedziałów, na które podzielony jest odcinek
to długości przedziałów, na które podzielony jest odcinek ![]() , a punkty
, a punkty ![]() to punkty wewnątrz tych przedziałów.
to punkty wewnątrz tych przedziałów.
Przy czym (i to jest bardzo ważne „przy czym”):
- długości wszystkich przedziałów
 muszą dążyć do 0 wraz ze wzrostem n
muszą dążyć do 0 wraz ze wzrostem n - ta suma musi być taka sama dla byle jak obranych przedziałów

- ta suma musi być taka sama dla byle jak obranych punktów
 wewnątrz przedziałów
wewnątrz przedziałów 
Zwróć uwagę na te dwa ostatnie warunki. Powiedzmy, że chcemy obliczyć – korzystając z definicji – prościutką całkę:
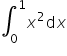
Na wykresie ta całka to było by pole zaznaczone poniżej:
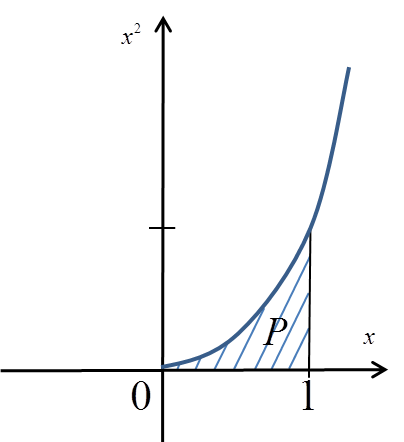
Aby obliczyć to pole z definicji, bez użycia dodatkowy twierdzeń, NIE wystarczyło by na przykład podzielić odcinek ![]() na
na ![]() RÓWNYCH odcinków (każdy miałby długość:
RÓWNYCH odcinków (każdy miałby długość: ![]() ):
):
![Pole pod funkcją x^2 w granicach od 0 do 1 z zaznaczonym podziałem przedziału [0,1] Pole pod funkcją x^2 w granicach od 0 do 1 z zaznaczonym podziałem przedziału [0,1]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/02/Obraz31.png)
NIE WYSTARCZY teraz obranie punktów ![]() na przykład równo w środku tych przedziałów:
na przykład równo w środku tych przedziałów:
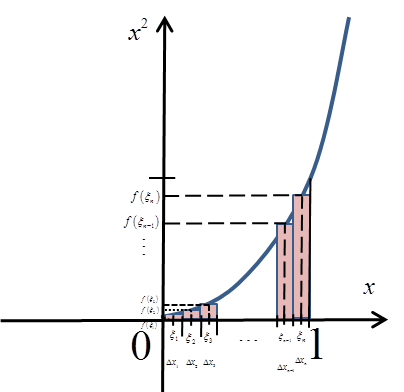
NIE WYSTARCZY obliczyć tak otrzymaną sumę całkową (czyli geometrycznie rzecz biorąc zsumować pola tych prostokątów):
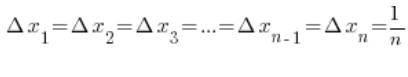 (odcinek o długości 1 dzielmy na
(odcinek o długości 1 dzielmy na ![]() równych części)
równych części)
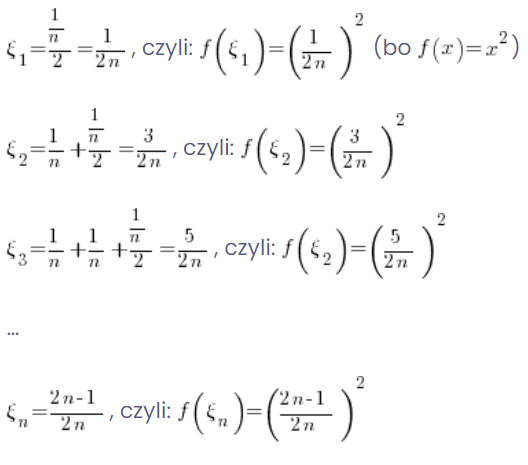
Moja suma będzie więc równa:
![]()
Korzystając ze wzoru na sumę kwadratów n kolejnych liczby nieparzystych (jest coś takiego):
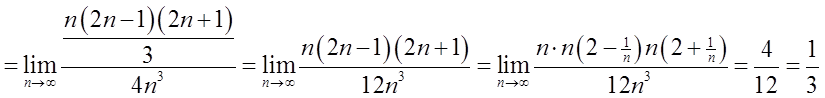
No ale to wszystko NIE WYSTARCZY (mimo, że oczywiście wynik jest dobry i to pole jest faktycznie równe ![]() ), aby policzyć z definicji całkę:
), aby policzyć z definicji całkę:
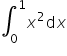
Dlaczego?
Przecież:
- Podzieliłem odcinek
 na 'n’ równych odcinków
na 'n’ równych odcinków - Wybrałem pośrodku każdego takiego odcinka punkt

- Obliczyłem sumę długości tych odcinków przemnożonych przez wartość funkcji w punktach
 (czyli pola prostokątów)
(czyli pola prostokątów) - Ta suma wyszła skończona (
 ), a długości 'n’ równych odcinków były nieskończenie małe przy 'n’ dążącym do nieskończoności
), a długości 'n’ równych odcinków były nieskończenie małe przy 'n’ dążącym do nieskończoności
Dlaczego więc nie mogę więc (jeszcze) stwierdzić, że:
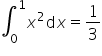
?
Ano niestety dlatego, że w samej definicji całki oznaczonej jest warunek, że owszem, suma całkowa ma być zbieżna (i jest), ale oprócz tego jest tam napisane, że ma być zbieżna do jednej i tej samej liczby dla dowolnego podziału przedziału ![]() i dla dowolnego wyboru punktów
i dla dowolnego wyboru punktów ![]() .
.
Ja natomiast jedyne co zrobiłem, to wykazałem, że suma jest zbieżna do ![]() dla jednego, wybranego przeze mnie podziału odcinkami
dla jednego, wybranego przeze mnie podziału odcinkami ![]() (był to akurat podział na równe części) i dla jednego, wybranego przeze mnie sposobu obrania punktów
(był to akurat podział na równe części) i dla jednego, wybranego przeze mnie sposobu obrania punktów ![]() (wybrałem sobie równo pośrodku przedziałów
(wybrałem sobie równo pośrodku przedziałów ![]() ).
).
Nie oznacza to jednak jeszcze, że:
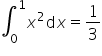
Aby to wykazać (na gruncie samej, samiusieńkiej definicji) musiałbym jakoś pokazać, że dla wszystkich sposobów podziału odcinka ![]() przedziałami
przedziałami ![]() i dla wszystkich możliwych wyborów punktów pośrednich
i dla wszystkich możliwych wyborów punktów pośrednich ![]() , zawsze i we wszystkich przypadkach suma całkowa równa jest
, zawsze i we wszystkich przypadkach suma całkowa równa jest ![]() .
.
Czy znasz już odpowiedź na pytanie testowe z początku wykładu:
czy liczenie całek oznaczonych przy jej pomocy jest:
a) Łatwe
b) Trudne
?
Oczywiście nie będę nawet próbować dobierać się do tak określonego samobójczego zadania. Potrzebuję czegoś więcej, dodatkowej artylerii. Będzie nią nowe twierdzenie (czyli z bólem serca wykraczam już poza samą, czystą definicję).
Twierdzenie o całkowalności funkcji ciągłej
Każda funkcja ciągła w przedziale
jest w tym przedziale całkowalna.
Twierdzenie proste jak konstrukcja cepa, prawda? Ale co właściwie z niego wynika i w czym może mi pomóc w obliczeniu z definicji całki:
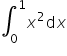 ?
?
Zapiszę je może innymi słowami i samo mi to wyjdzie:
Jeżeli funkcja
jest ciągła w przedziale
, to dla dowolnego podziału odcinka
przedziałami
i dla dowolnego wyboru punktów pośrednich
jej suma całkowa zbiega do tej samej liczby.
Prawda? Bo taki jest właśnie sens słowa „całkowalna”. A logicznym wnioskiem z powyższego twierdzenia jest:
- Jeżeli funkcja jest ciągła na przedziale

- Jeżeli znalazłem taki jeden z możliwych podziałów przedziałami
 i punktami
i punktami  , dla którego suma całkowa zbiega do pewnej liczby,
, dla którego suma całkowa zbiega do pewnej liczby,
to:
Zgodnie z twierdzeniem o całkowalności funkcji ciągłej dla każdego innego podziału każda „inna” suma całkowa będzie zbiegać do tej samej liczby (bo jeśli jest ciągła, to dla dowolnego zbiega do tej samej)!
Czyli – mając funkcję ciągłą – możesz obliczyć jej sumę całkową dla dowolnego wybranego przez Ciebie podziału (np. podziału na równe odcinki i punktach pośrednich pośrodku), powołać się na twierdzenie o całkowalności funkcji ciągłej i wyznaczyć w ten sposób (w końcu) całkę oznaczoną z definicji.
Wracając więc do mojego przykładu na całkę:
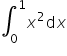
Wszystko było w porządku i wszystkie obliczenia były ważne, na końcu jednak trzeba by jeszcze dopisać:
Zgodnie z twierdzeniem o całkowalności funkcji ciągłej (funkcja ![]() jest oczywiście funkcją ciągłą na przedziale
jest oczywiście funkcją ciągłą na przedziale ![]() ), z tego, że suma całkowa dla wybranego przeze mnie podziału na
), z tego, że suma całkowa dla wybranego przeze mnie podziału na ![]() i
i ![]() wyszła równa
wyszła równa ![]() wynika, że dla dowolnego innego podziału też jest ona równa
wynika, że dla dowolnego innego podziału też jest ona równa ![]() , a więc:
, a więc:
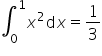
Dowód twierdzenia o całkowalności funkcji ciągłej odłożę sobie na inny raz.
Teraz pokażę Ci dwa inne przykłady na obliczanie całki oznaczonej z definicji.
Przykład 2
Oblicz z definicji:
.
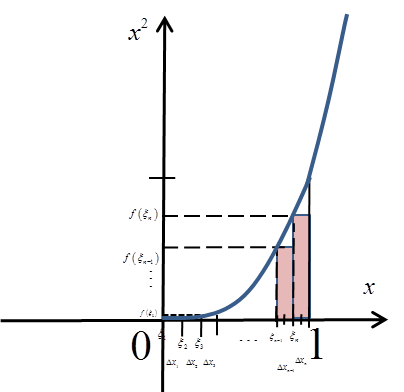
Dzielę odcinek ![]() na n równych części i punkty
na n równych części i punkty ![]() obieram równo na początku każdego przedziału
obieram równo na początku każdego przedziału ![]() :
:
Mam więc dla funkcji ![]() :
:
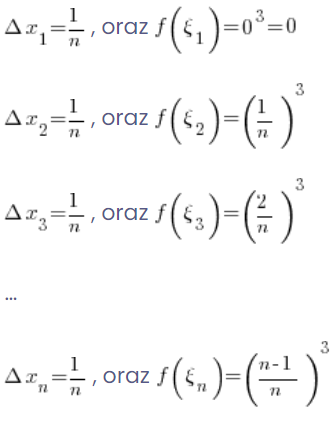
Moja suma całkowa będzie więc równa:
![]()
Korzystam ze wzoru na sumę sześcianów kolejnych liczb naturalnych (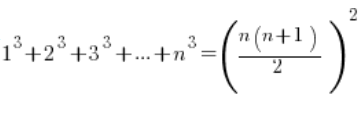 ), zmodyfikowanego, bo wyrazów mam n-1:
), zmodyfikowanego, bo wyrazów mam n-1:
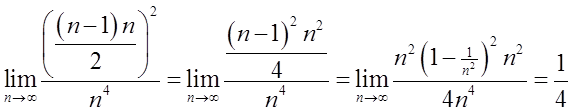
Funkcja ![]() jest funkcją ciągłą na przedziale
jest funkcją ciągłą na przedziale ![]() .
.
Zgodnie z twierdzeniem o całkowalności funkcji ciągłej:
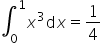
Przykład 3
Oblicz z definicji:
.
Dzielę odcinek ![]() na n równych części i punkty
na n równych części i punkty ![]() obieram na końcu każdego przedziału
obieram na końcu każdego przedziału ![]() :
:
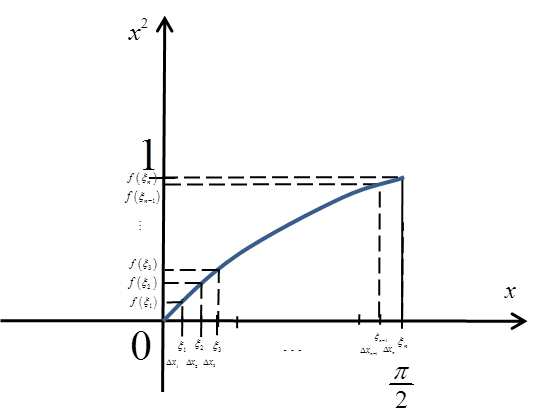
Mam więc dla funkcji ![]() :
:
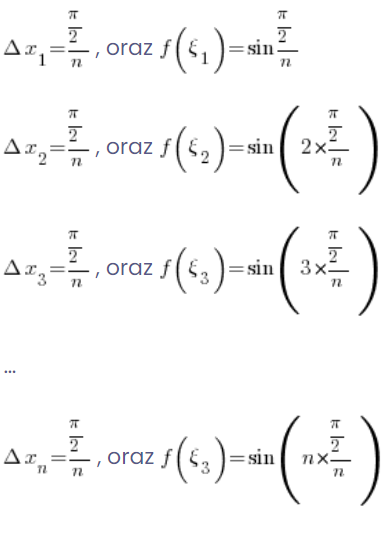
Moja suma całkowa będzie więc równa:
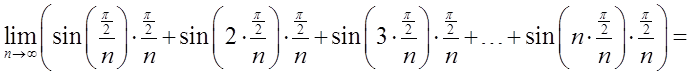
Jest ona oczywiście ciężka, ale pomocny będzie wzór (można wykazać go indukcyjnie):
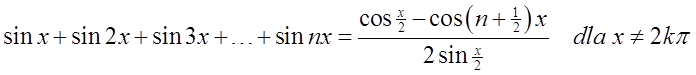
Po skorzystaniu z tego wzoru, będę miał:
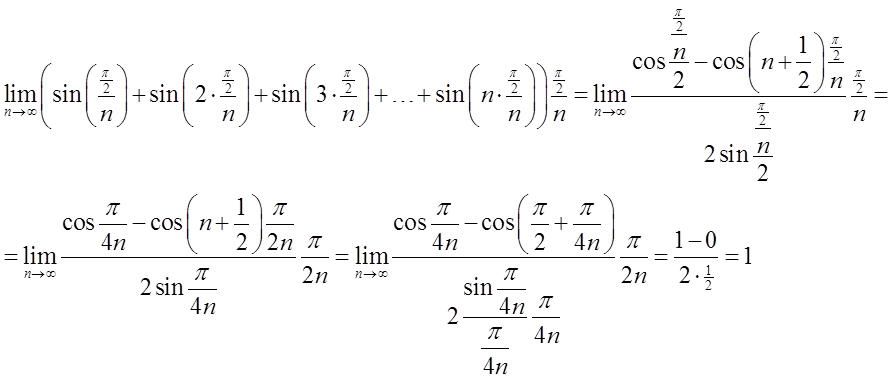
Zatem, zgodnie z twierdzeniem o całkowalności funkcji ciągłej:
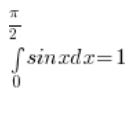
KONIEC
Pisząc tego posta korzystałem z…
1. „Rachunek różniczkowy i całkowy. Tom II.” G.M. Fichtenholz. Wyd. 1966.
Kliknij, aby przypomnieć sobie definicję całki oznaczonej (poprzedni Wykład) <–
Kliknij tutaj, aby powrócić na stronę z wykładami o całkach oznaczonych


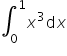 .
.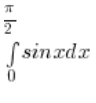 .
.
Dziękuję za ten wykład 🙂 Bardzo się przydał 🙂 Pozdrawiam !