Цей пост уже третій поспіль, у якому я хочу звернути вашу увагу на речі, які варто повторити на самому початку вивчення математики в університеті. Швидке повторення цих тем значно полегшить ваше життя в університеті. У попередніх постах я розглянув теми:
Геометрична інтерпретація абсолютної величини
Сьогодні черга за квадратичною функцією.
Квадратична функція? Але ми ж це, здається, два місяці робили…
Тема квадратичної функції, звісно, дуже широка, і я зовсім не маю на увазі, що потрібно взяти підручник зі школи і переглянути весь розділ від початку до кінця.
Зосередимося лише на кількох важливих деталях, нюансах і пастках.
Квадратична функція та квадратичне рівняння
Квадратична функція – це, звісно, щось таке:
![]() або:
або: 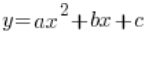
Де ![]() – це будь-які числа. Приклади квадратичних функцій:
– це будь-які числа. Приклади квадратичних функцій:
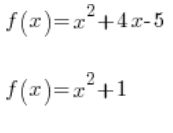
тощо…
Поняття квадратичної функції слід відрізняти від поняття квадратичного рівняння, наприклад:
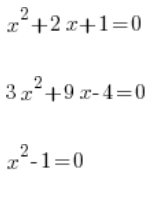
тощо…
Це не те саме!!!!
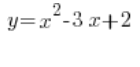 – це квадратична функція, а
– це квадратична функція, а 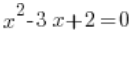 – це квадратичне рівняння.
– це квадратичне рівняння.
Нерозрізнення функції від рівняння часто призводить до…
Жахлива помилка номер 1
Наприклад, обчислюючи похідні та маючи дану функцію:
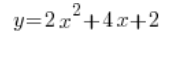
Люди часто роблять щось подібне:
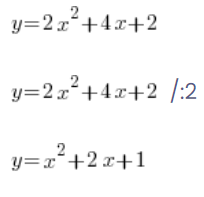
…і далі обчислюють, що потрібно.
Вони помиляються, тому що пам’ятають, що можна було робити таке з рівняннями:
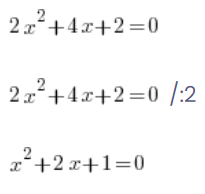
…і з рівняннями все добре, можна ділити обидві сторони, 0 праворуч поділене на 2 дійсно дає 0 і рівняння є еквівалентними (мають однакові розв’язки).
Але цей трюк не можна виконувати з функціями – потрібно ж якось поділити також це y зліва і т.д. Проста ділення значення функції на 2 дає іншу функцію!
Що слід повторити з функцій?
Не так багато. Власне, тільки дві форми функцій: канонічна та множинна.
Канонічна форма квадратичної функції
Припускаю, що ми вже маємо загальну форму квадратичної функції:
![]()
Її канонічна форма:
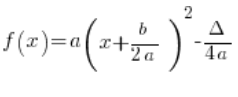
Тобто:
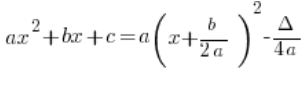
Що таке a, b і ![]() – це якось так зрозуміло, мало хто має проблему з тим, що
– це якось так зрозуміло, мало хто має проблему з тим, що ![]() .
.
Можна навіть помітити, що якщо в канонічній формі винести ![]() перед дужкою, отримаємо:
перед дужкою, отримаємо:
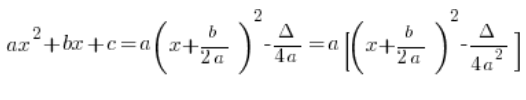
…що іноді може бути корисним, а іноді не обов’язково.
Якщо ти навчався цього, обчислюючи координати вершини (зазвичай як ![]() і
і ![]() ) і вставляючи у формулу:
) і вставляючи у формулу:
![]() то, звичайно, це трохи обхідний шлях, але також добре.
то, звичайно, це трохи обхідний шлях, але також добре.
Запам’ятай ![]() на початку формули канонічної форми!
на початку формули канонічної форми!
Множинна форма квадратичної функції (її розкладання на множники):
Повертаючись тепер до нашої загальної квадратичної функції:
![]()
Дуже часто потрібно буде “розкласти її на множники”, використовуючи множинну форму квадратичної функції:
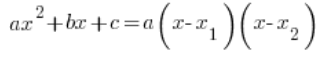
Де ![]() і
і ![]() обчислюємо з відомих і улюблених формул:
обчислюємо з відомих і улюблених формул:
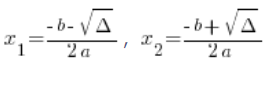
Тут також потрібно пам’ятати про ![]() на початку формули!!!
на початку формули!!!
Зверніть увагу також, що ці ![]() і
і ![]() не завжди існують (якщо дельта від’ємна, вони не існують), тобто функцію не завжди можна записати у множинній формі, тобто квадратичну функцію не завжди можна розкласти на множники.
не завжди існують (якщо дельта від’ємна, вони не існують), тобто функцію не завжди можна записати у множинній формі, тобто квадратичну функцію не завжди можна розкласти на множники.
Що слід повторити з квадратичних рівнянь?
З квадратичними рівняннями, я припускаю, справи не так погано. Ми зазвичай справляємося з розв’язанням загального рівняння:
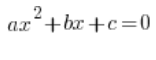
Наприклад:
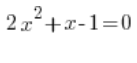
Ми просто обчислюємо:
![]()
А потім, якщо дельта виявилася невід’ємною, розв’язки рівняння:
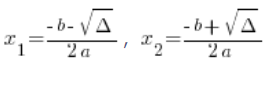
Пам’ятай, що там внизу у знаменнику є ![]() а не просто 2!
а не просто 2!
Однак я хотів би зупинитися на особливому випадку рівняння:
![]()
Тут виникає багато помилок. Наприклад:
Жахлива помилка номер 2
![]()
![]()
У чому полягає помилка? Число 2 дійсно є розв’язком рівняння ![]() , але було повністю пропущено другий розв’язок цього рівняння, а саме число -2. Повинно бути:
, але було повністю пропущено другий розв’язок цього рівняння, а саме число -2. Повинно бути:
![]()
![]()
Негативні розв’язки можна пропускати тільки в геометрії (тому що відстань не може бути від’ємною).
Ще одна проблема з рівнянням у формі: ![]() це:
це:
Жахлива помилка номер 3
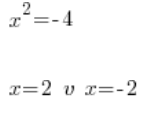
Що, звісно, є нісенітницею, оскільки 2 у квадраті не дає -4. Взагалі нічого у квадраті не дає -4 (ті, хто вже вивчав комплексні числа, мовчіть). Рівняння:
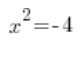
…не має розв’язків.
Тому потрібно бути пильним. Рівняння ![]() має два розв’язки, а рівняння
має два розв’язки, а рівняння ![]() взагалі не має розв’язків.
взагалі не має розв’язків.
Запрошую до спокійного повторення всього, що було сказано до цього часу і, звісно, до питань у коментарях.


