Місце і час дії
Обчислення напрямних похідних як тема для вивчення (тобто для здачі) розташовані безпосередньо після часткових похідних функцій багатьох змінних, які більшість студентів вивчають у другому семестрі.
Це тема настільки рідко розглядається, що я не включив її в свій Курс часткових похідних, але настільки часто, що я додам її в блог – на користь тих, хто повинен вивчати напрямні похідні, і тих, хто просто цікавиться, про що йдеться. Однак, як і в курсах, сьогодні я майже виключно зосереджуся на практиці (“як це зробити?”), а не на теорії (“що я насправді роблю?”).
Напрямні похідні – як я маю це зробити?
У випадку напрямної похідної ми маємо справу з одночасним приростом аргументів x і y, що, звичайно, відповідає певному приросту значення функції 
.
Для виконання завдання нам потрібні три речі:
- Функція, з якої ми будемо рахувати напрямну похідну.
- Точка, в якій ми будемо рахувати напрямну похідну.
- Напрямок, заданий у вигляді вектора.
Маючи вищезазначене, завдання зводиться до перетворення вектора у напрямний вектор (щось з аналітичної геометрії, я покажу, як це зробити за мить), а потім підставлення у формулу:
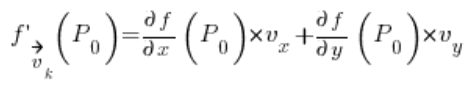
У якій:
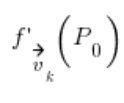це напрямна похідна в точці 
в напрямку вектора 
це точка, в якій ми рахуємо напрямну похідну
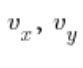це координати напрямного вектора
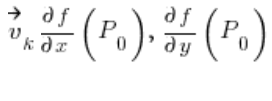це часткові похідні функції в точці .
Обчисліть напрямну похідну функції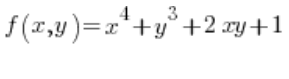 
в точці P(1,2) в напрямку 
.
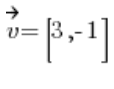Рішення:
Все готово, потрібно лише перетворити вектор 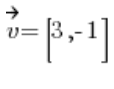на напрямний вектор.
Напрямний вектор – це вектор з тим самим напрямком (хто б міг подумати), тією ж орієнтацією, але з довжиною 1.
Його обчислюють за формулою:
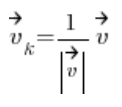
Просто ділять його координати на його довжину.
Отже, обчислюємо довжину вектора :
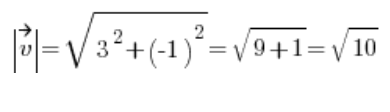
Потім отримуємо напрямний вектор:
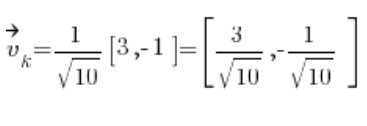
Для формули напрямної похідної нам також потрібні часткові похідні функції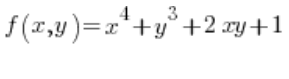 в точці P(1,2):
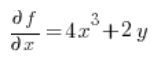
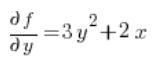
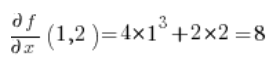
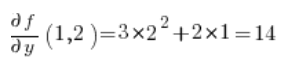
Тепер ми маємо все, що потрібно для формули:
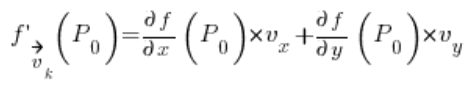
Просто підставляємо, і ми маємо результат: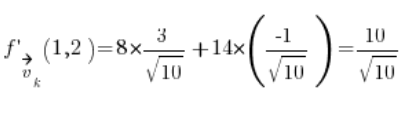 
.
Готово.
Приклад 2
Знайдіть напрямну похідну функції: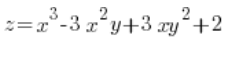 
в точці P(3,1) в напрямку від цієї точки до точки Q(6,5).
Рішення:
Завдання трохи складніше, тому що напрямний вектор не заданий безпосередньо, але для нас це не проблема.
Ми пересуваємось від точки P до точки Q, отже, вектор зсуву – це вектор [3,4].
Тепер ми знаходимо напрямний вектор, обчислюючи довжину вектора [3,4]:
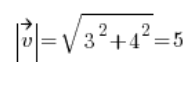
І ми маємо напрямний вектор:
Тепер обчислюємо часткові похідні в точці (3,1):
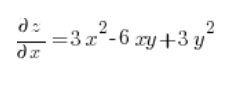
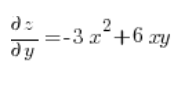
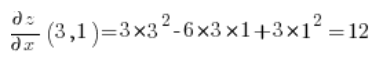
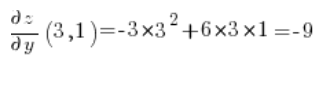
Потім просто підставляємо у формулу напрямної похідної:
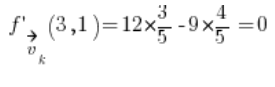
Приклад 3
Знайдіть напрямну похідну функції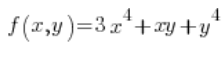 
в точці (1,2) в напрямку, який утворює кут 
з додатною піввіссю x.
Рішення:
Завдання здається складнішим через відсутність напрямного вектора в даних. Давайте намалюємо всю річ:
Йдеться про те, щоб знайти координати будь-якого вектора в заданому напрямку.
Ми використовуємо той факт, що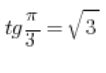 
і можемо припустити, що наш вектор має координати 
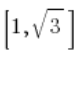, як на малюнку (було достатньо вибрати будь-який вектор у напрямку прямої):
І тепер ми продовжуємо по-старому.
Обчислюємо напрямний вектор:
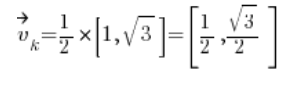
Потім часткові похідні в точці (1,2):
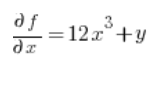
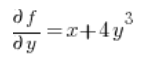
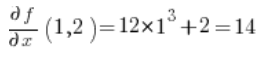
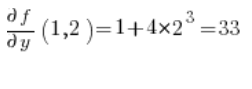
Підставляємо у формулу і отримуємо результат
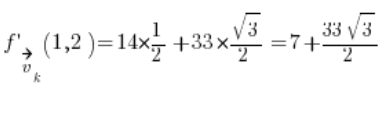
Запрошую до питань у коментарях – як завжди 🙂
