Немає товарів у кошику.
Krystian Karczyński- 18 Квітня 2024
- Komentarz 0
При вирішенні завдань за допомогою комплексних поліноміальних рівнянь ми загалом використовуємо ті ж методи, що й для розв’язання реальних поліноміальних рівнянь у середній школі.
Комплексні рівняння четвертого ступеня, які можна звести до другого ступеня
Це також стосується комплексних рівнянь четвертого ступеня, які можна звести до рівнянь другого ступеня, тобто таких, де ми маємо змінну в четвертій степені, в другій степені та вільний член, наприклад:
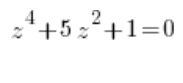
або:
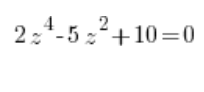
Ми зводимо такі типи складних рівнянь до комплексних рівнянь другого ступеня за допомогою підстановки 
, де 
звісно є комплексною змінною.
Завдання
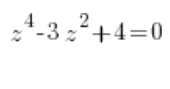
Ми робимо підстановку (звісно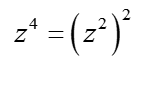 
), отже ми отримуємо:
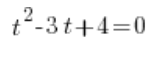
І отже ми вирішуємо це рівняння звичайним способом за допомогою дискримінанта (звісно, корені від’ємних чисел існують у комплексних числах). Ми отримаємо два комплексні розв’язки:
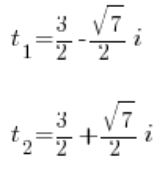
Оскільки ми зробили підстановку: , у нас є:
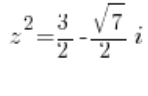
або:
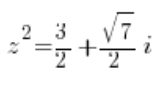
тобто:
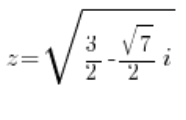
або:
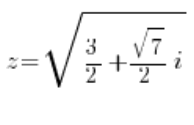
Після обчислення коренів (звичайно, вийдуть чотири комплексні корені) ми матимемо чотири розв’язки:
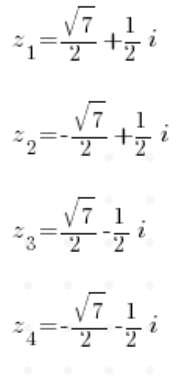
П.С. Я показую цей та інші методи у Уроці 6 мого Курсу Комплексних Чисел, запрошую вас!
