Об’єм еліпсоїда (але не обертового, а дикого типу) обчислений визначеним інтегралом
Krystian Karczyński
Засновник та керівник сервісу eTrapez.
Магістр математики Познанської Політехніки (Польща). Репетитор з математики з багаторічним досвідом. Творець перших Курсів eTrapez, які здобули величезну популярність серед студентів у всій Польщі.
Живе у Щецині (Польща). Любить прогулянки лісом, відпочинок на пляжі та каякінг.
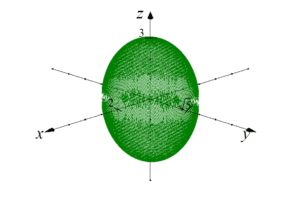
Скажімо, нам потрібно обчислити об’єм еліпсоїда:
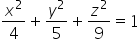
Цей еліпсоїд перетинає осі x, y, z в координатах 2, 
і 3 (загальне рівняння еліпсоїда: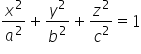 
, де a, b, c – координати перетину).
Це не обертовий еліпсоїд, він не утворюється обертанням будь-якої кривої навколо будь-якої осі, тому ми не можемо використовувати стандартну формулу для об’єму обертового тіла:
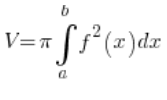
Нам потрібно шукати інший спосіб.
1. Обираємо будь-яку точку M(z) в центрі еліпсоїда і на осі OZ.
Площина, що проходить через цю точку і перпендикулярна осі OZ, “вирізає” нам певний еліпс з еліпсоїда:
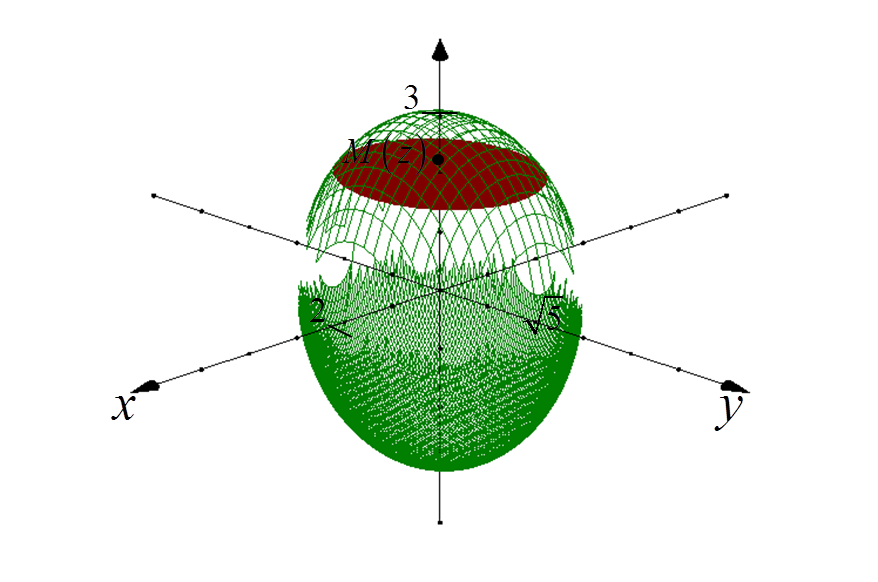
2. Визначаємо рівняння проекції “вирізаного” еліпса на площину XY
Ми визначаємо рівняння цього еліпса для фіксованого ‘z’ (вважаємо ‘z’ за константу) з загального рівняння еліпсоїда:
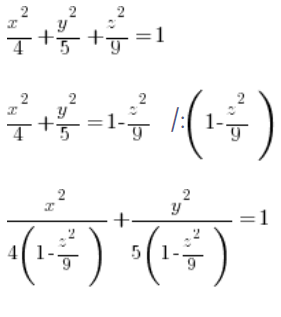
Видно, що наші ‘a’ і ‘b’ з загального рівняння еліпсоїда (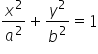
) це:
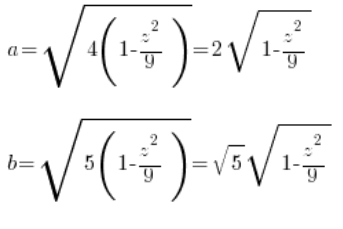
4. Обчислюємо площу цього перерізу в залежності від змінної ‘z’
Площа цього еліпса залежатиме від обраної точки ‘z’, тобто це буде функція змінної ‘z’. Ми можемо обчислити її або за готовою формулою площі еліпса (
):
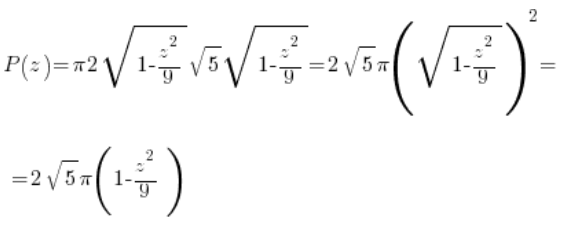
Або обчислюючи відповідний визначений інтеграл (звичайно ж, використовуючи параметричну форму еліпса і формулу площі області в параметричній формі):
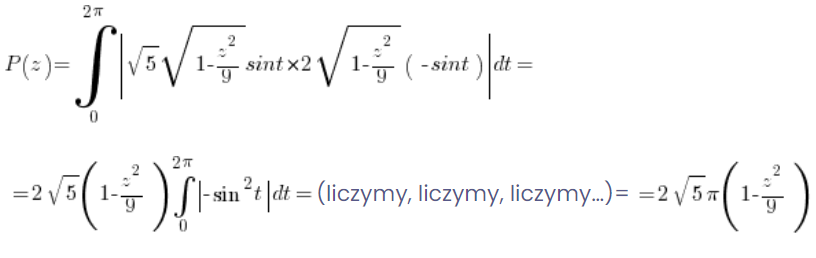
5. Обчислюємо об’єм тіла за допомогою площ перерізів
Тепер найскладніше. Об’єм тіла дорівнює – це трохи некрасиво звучить – “сумі” (тобто інтегралу) всіх перерізів, загалом:
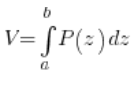
де 
є функцією площ перерізів тіла площиною, перпендикулярною до осі OZ, а ‘a’ і ‘b’ – це межі, в яких змінюється ‘z’.
Тобто у нас:
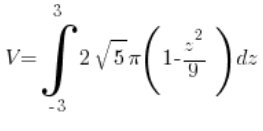= (рахуємо, рахуємо, рахуємо…) = 
Це відповідає загальній формулі для еліпсоїда (
).
КІНЕЦЬ
Варто запам’ятати цю загальну схему, і, перш за все, що об’єм складніших, не обертових тіл можна обчислити, інтегруючи функцію їх площ перерізів.
Шукаєте репетитора з математики для університетського рівня або школи? А може вам потрібен курс, який підготує вас до вступних іспитів?
Ми - команда eTrapez. Ми вчимо математику ясно, просто і дуже детально - дістанемося навіть до найбільш відсторонених від знань.
Ми створили курси відео зрозумілою мовою для завантаження на комп'ютер, планшет або телефон. Вмикайте запис, дивіться і слухайте, як на репетиторстві. У будь-який час дня та ночі.
