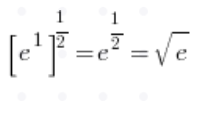Типові межі послідовностей з формулою для числа e
Традиційні задачі на межі послідовностей з формулою для числа e досить “природно” призводять до формули (показую, як це робити в своєму Курсі):
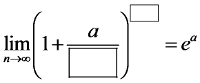Але що робити, коли в дужках у нас немає такого елегантного дробу, а щось типу:
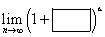Якщо прямокутник у дужках прямує до нуля, а трикутник у показнику прямує до нескінченності, ми маємо насправді невизначений символ 
– саме той, в якому застосовуємо формулу з числом ‘e’ у результаті. Що робити?
Ну, згадаймо, що будь-який вираз можна представити як ділення одиниці на обернений вираз 🙂
Наприклад, звичайне, чемне число 2 можна записати як:
Отже, будь-який вираз можна “силоміць” зробити дробом, якщо це дійсно потрібно.
Приклад нетипової межі з формулою для числа e
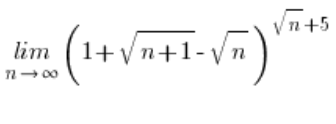
Спершу варто було б показати, що вираз 
прямує до нуля. Ти зробиш це, обчисливши межу:
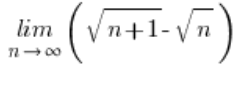– результат буде дійсно дорівнювати нулю (можна застосувати метод множення на спряження).
Тепер замінюєш:
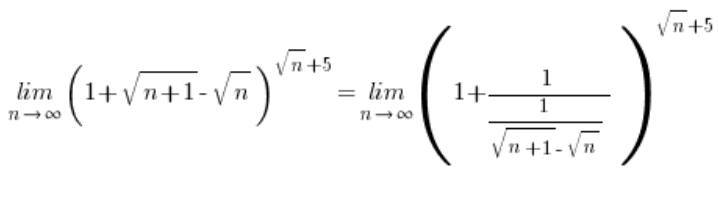
… і далі вже за відомою схемою:
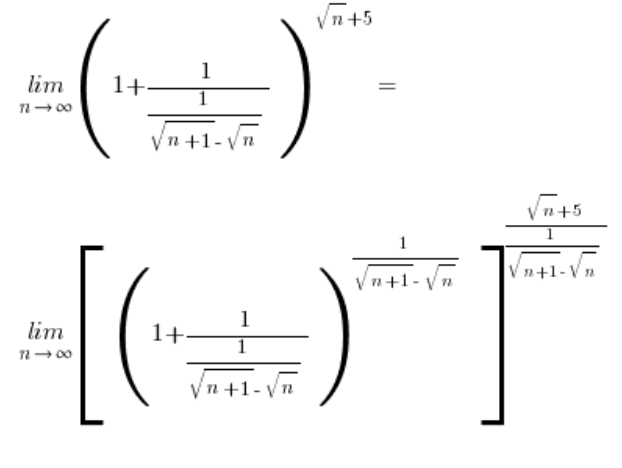
Межа у великій квадратній дужці дорівнює: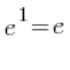 
– згідно з основною формулою, залишається тільки перехід до:
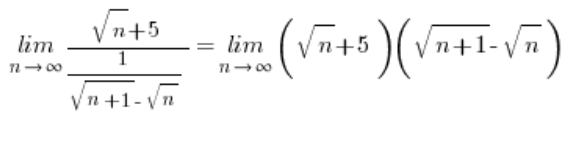
… який після застосування множення на спряження закінчиться результатом 
.
Отже, вся межа дорівнює:
