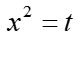Немає товарів у кошику.
Krystian Karczyński- 28 Червня 2024
- Komentarz 0
У невизначених раціональних інтегралах, як ми знаємо, часто необхідно розкласти знаменник підінтегральної функції на множники і далі розкласти на прості дроби.
Але розклад на множники сам по собі може бути часто проблематичним.
Типові ситуації
Для простих ситуацій, таких як:
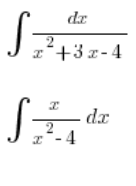
Ми впораємося:
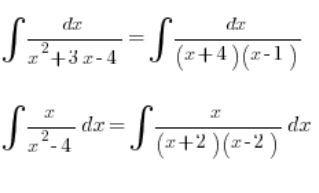
Якщо в знаменнику буде поліном третього ступеня, відповідно “налаштований”, ми також впораємося:
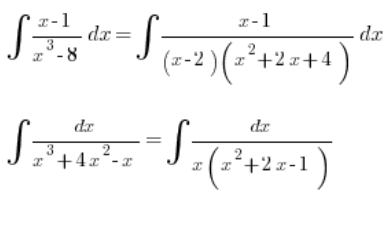
Знаменник з непривітним поліномом третього ступеня
Проблема починається тоді, коли в знаменнику знаходиться поліном третього ступеня, який складно розкласти на множники, наприклад:
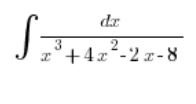
Глибокий вдих.
Контролюй паніку.
Такі речі (розкладання такого типу поліномів на множники) робили вже в середній школі і на базовому рівні.
Потрібен лише хитрий трюк:
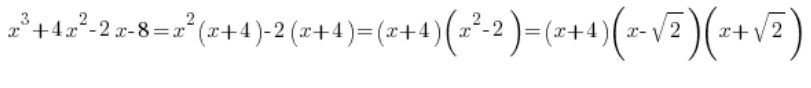
Пам’ятаєш? Звичайно…
Отже, ми можемо розкласти поліном в знаменнику:
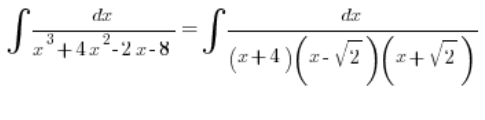
І далі впевнено розкладати на три прості дроби, як нам вказують правила.
Ще складніший розклад на множники
А як щодо такої ситуації? Пам’ятаєш зі школи (це вже розширений рівень)?
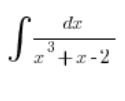
Тут було трохи гірше. Середній компонент треба було розбити на два:
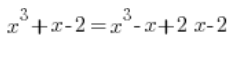
І далі як зазвичай:
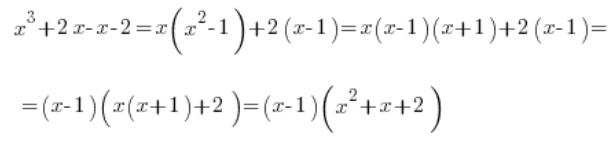
Тобто інтеграл треба записати так:
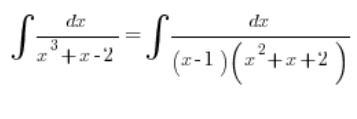
І спокійно далі рахувати.
Методи розкладу знаменника на множники в раціональних інтегралах
Загалом пам’ятай в раціональних інтегралах, що якщо доводиться розкладати на множники поліном, всі шкільні хитрощі дозволені, а також можуть бути, наприклад:
- розклад деяких поліномів 4-го ступеня через допоміжну підстановку
- пошук “наосліп” кореня і ділення поліному, щоб знизити його ступінь
Звісно, ми говоримо зараз лише про складніші невизначені раціональні інтеграли, які в багатьох (більшості?) університетах навіть не вводяться!
Related Posts
