Немає товарів у кошику.
Krystian Karczyński- 2 Липня 2024
- Komentarz 0
Розв’язуючи задачі з комплексними числами, треба мати на увазі, що комплексне число в тригонометричній формі виглядає так:
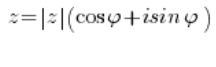
І тільки так. Ні більше, ні менше.
Отже, потрібно звернути увагу на:
Коли комплексне число є, а коли не є в тригонометричній формі?
- Число: Є числом у тригонометричній формі, в якій модуль числа дорівнює 1 (), бо очевидно:
- Число: НЕ є числом у тригонометричній формі, бо перед уявною одиницею ‘i’, помноженою на синус, стоїть мінус, а повинен бути плюс.
Щоб перетворити це число на тригонометричну форму, потрібно скористатися тригонометричними формулами:
Використовуючи ці формули, ми можемо перетворити:
Функції синуса і косинуса є-періодичними, отже їх значення такі ж, як . Більше про це я написав у: цьому дописі.
Отже, в кінці ми маємо:
…а це вже є число в тригонометричній формі. - Число: НЕ є числом у тригонометричній формі, бо перед уявною одиницею ‘i’, помноженою на синус, стоїть мінус, а повинен бути плюс, а також перед косинусом стоїть мінус, а повинен бути плюс.
Щоб перетворити це комплексне число на тригонометричну форму, потрібно винести мінус перед дужками:
Замінити збоку число на тригонометричну форму (це ми вже вміємо…):
Отже, у нас є множення двох чисел у тригонометричній формі:
А множимо числа в тригонометричній формі, множачи їх модулі і додаючи аргументи (для цього є формула), отже, маємо:
Це вже є число в тригонометричній формі. - Число: НЕ Є комплексним числом у тригонометричній формі, тому що перед косинусом стоїть мінус, а повинен бути плюс.
Щоб перетворити це комплексне число в тригонометричну форму, потрібно винести мінус перед дужками:
Число -1 потрібно перетворити в тригонометричну форму (ми це зробили в пункті 3), аналогічно потрібно перетворити число в тригонометричну форму (ми це зробили в пункті 2).
Отримуємо:
Використовуючи формулу для множення тригонометричних функцій:
І використовуючи періодичність функцій синуса і косинуса:
- Число: НЕ Є комплексним числом у тригонометричній формі, бо перед косинусом стоїть уявна одиниця ‘i’ (яка не повинна там бути), а перед синусом немає уявної одиниці ‘i’.
Потрібно скористатися тригонометричними формулами, відомими зі школи:
Отже, маємо:
І це вже Є комплексне число у тригонометричній формі. - Число: НЕ Є комплексним числом у тригонометричній формі.
Потрібно замінити синус на косинус так, як ми це зробили в пункті 5, а потім розв’язати як у пункті 4. - Число: НЕ Є комплексним числом у тригонометричній формі.
Потрібно замінити синус на косинус так, як ми це зробили в пункті 5, а потім розв’язати як у пункті 2. - Число: НЕ Є комплексним числом у тригонометричній формі.
Потрібно замінити синус на косинус так, як ми це зробили в пункті 5, а потім розв’язати як у пункті 3.
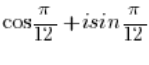Є числом у тригонометричній формі, в якій модуль числа дорівнює 1 (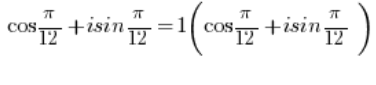
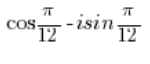), бо очевидно:
НЕ є числом у тригонометричній формі, бо перед уявною одиницею ‘i’, помноженою на синус, стоїть мінус, а повинен бути плюс.
-періодичними, отже їх значення такі ж, як 
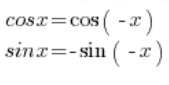
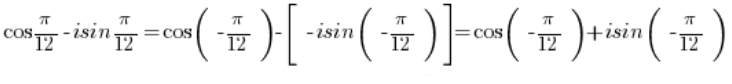
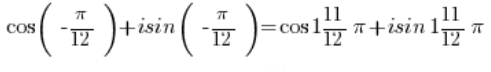
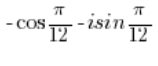НЕ є числом у тригонометричній формі, бо перед уявною одиницею ‘i’, помноженою на синус, стоїть мінус, а повинен бути плюс, а також перед косинусом стоїть мінус, а повинен бути плюс.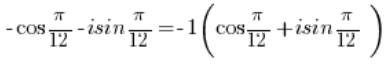
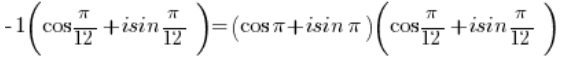
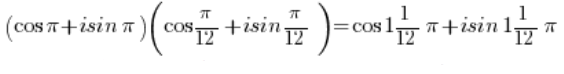
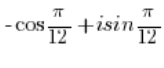на тригонометричну форму (це ми вже вміємо…):
НЕ Є комплексним числом у тригонометричній формі, тому що перед косинусом стоїть мінус, а повинен бути плюс.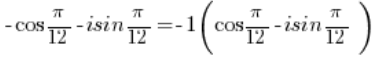
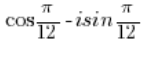в тригонометричну форму (ми це зробили в пункті 2).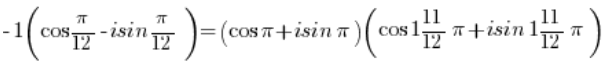
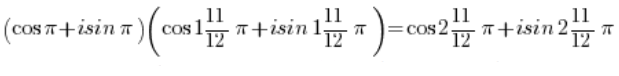
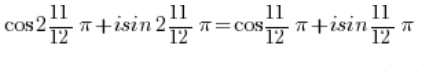
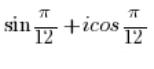НЕ Є комплексним числом у тригонометричній формі, бо перед косинусом стоїть уявна одиниця ‘i’ (яка не повинна там бути), а перед синусом немає уявної одиниці ‘i’.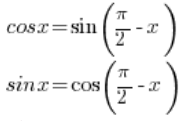
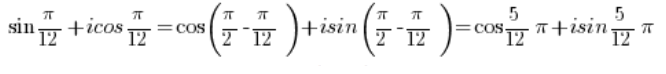
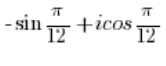НЕ Є комплексним числом у тригонометричній формі.
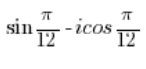НЕ Є комплексним числом у тригонометричній формі.
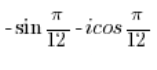НЕ Є комплексним числом у тригонометричній формі.Удачі! 🙂
