Підстановки Ейлера I, II, III типів – Більше не потрібно
У попередніх постах я показав, як використовувати підстановки Ейлера у інтегралах типу:

- Підстановки Ейлера I типу (коли a>0)
- Підстановки Ейлера II типу (коли c>0)
У цьому пості ми розглянемо третій і останній тип підстановок Ейлера, які ми можемо використовувати, коли у інтегралі:

квадратний тричлен ![]() , має два різні корені
, має два різні корені ![]() , тобто коли його
, тобто коли його  , тобто коли його можна записати у вигляді добутку:
, тобто коли його можна записати у вигляді добутку: ![]() .
.
Але перед тим як перейти до справи, зауважимо, що ці три випадки:
- I тип, коли a>0
- II тип, коли c>0
- III тип, коли є два різні корені
дозволяють нам розв’язати будь-який інтеграл типу:

Насправді навіть лише I і III типи достатні.
Чому?
Випадок, коли ![]() можна оминути, оскільки квадратний тричлен
можна оминути, оскільки квадратний тричлен ![]() просто перетворюється на лінійну форму
просто перетворюється на лінійну форму ![]() , яку ми розв’язуємо простішими підстановками, ніж Ейлера.
, яку ми розв’язуємо простішими підстановками, ніж Ейлера.
Але що робити, коли a<0 (не підходить до I типу) і квадратний тричлен має один або взагалі не має коренів (не підходить до III типу)?
Тоді його графік виглядав би так (пам’ятаємо з середньої школи – гілки вниз):
або, якщо взагалі не мав би коренів, так:
Який з цього висновок? Що в обох випадках квадратний тричлен приймав би негативні значення (за винятком, щонайбільше одного пункту), а я нагадую, що ми рахуємо інтеграл:

Тобто, у підінтегральній функції квадратний тричлен знаходиться під коренем, а корінь не може бути знайдений з негативних значень (звісно, ми граємо з дійсними числами). Тобто, область визначення такої функції була б щонайбільше одним пунктом, тобто взагалі без сенсу, і такого прикладу ми точно не отримаємо. Хіба що професор буде дійсно дуже втомлений при складанні прикладів на іспиті.
Отже, випадок, коли a<0 і квадратний тричлен ![]() не має двох коренів, можна оминути, і тепер явно видно, що I і III типи підстановок Ейлера підходять до БУДЬ-ЯКОГО інтегралу типу:
не має двох коренів, можна оминути, і тепер явно видно, що I і III типи підстановок Ейлера підходять до БУДЬ-ЯКОГО інтегралу типу:

До справи, отже, беремося за III тип підстановок Ейлера.
Підстановки Ейлера III типу
Маємо інтеграл:
 ,
,
де ![]() має
має  , тобто можна його записати як:
, тобто можна його записати як:
![]() ,
,
де ![]() це його корені.
це його корені.
Підстановка, яку ми тут використовуємо, це:
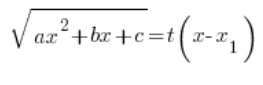
Підносимо обидві сторони цієї підстановки до квадрату, квадратний тричлен зліва записуємо у вигляді добутку (знаємо, що можна), ділимо обидві сторони на ![]() і продовжуємо, як у попередніх типах підстановок, визначаючи послідовно:
і продовжуємо, як у попередніх типах підстановок, визначаючи послідовно:
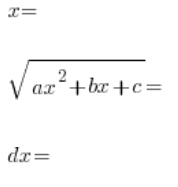
На кінці підставляємо все до вихідного інтегралу і отримуємо – зазвичай клопіткий – раціональний інтеграл.
До роботи.
Приклад
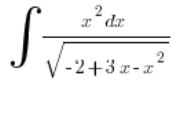
Наше ![]() (тобто a<0, тобто не застосовуємо підстановки I типу), наше
(тобто a<0, тобто не застосовуємо підстановки I типу), наше ![]() (тобто c<0, тобто не застосовуємо підстановки II типу), але наша
(тобто c<0, тобто не застосовуємо підстановки II типу), але наша ![]() , тобто можемо застосувати підстановки III типу.
, тобто можемо застосувати підстановки III типу.
Рахуємо спочатку ![]() :
:
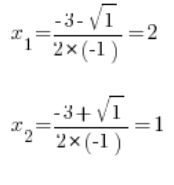
Застосовуємо підстановку Ейлера III типу:
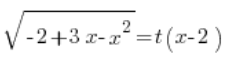
Підносимо обидві сторони до квадрату:
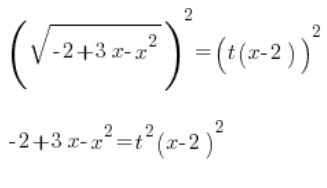
Квадратний тричлен зліва записуємо у вигляді добутку (пам’ятати про ![]() тут!!!):
тут!!!):
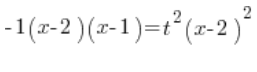
Ділимо обидві сторони на ![]() :
:
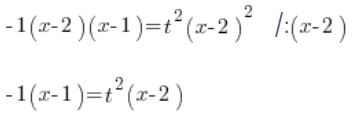
Визначаємо ![]() :
:
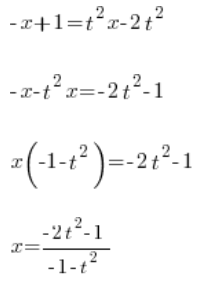
Маємо ![]() визначене за допомогою змінної
визначене за допомогою змінної ![]() . Тепер беремося за визначення
. Тепер беремося за визначення 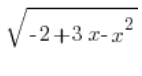 .
.
Повертаючись до нашої першої підстановки, маємо, що:
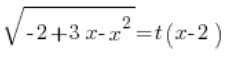
Вставляємо визначене 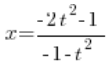 , і маємо:
, і маємо:
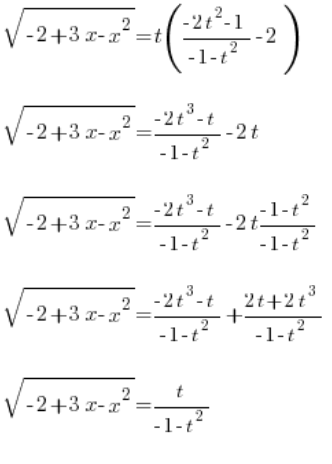
Маємо цілком акуратно визначене 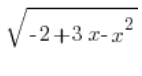 . Тепер вже лише
. Тепер вже лише ![]() , яке порахуємо, визначаючи похідну з
, яке порахуємо, визначаючи похідну з ![]() :
:
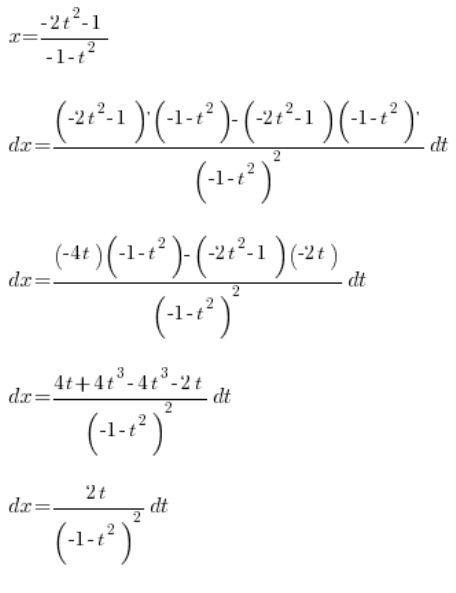
Отже, ми визначили:
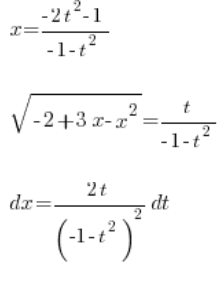
, все за допомогою змінної ![]() . Вставляємо це до інтегралу:
. Вставляємо це до інтегралу:
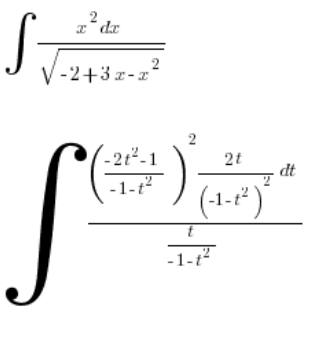
Спрощуємо:
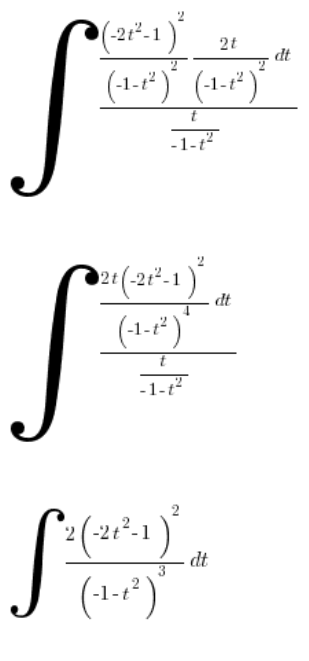
Згідно з передбаченнями, ми отримуємо дійсно складний раціональний інтеграл, який я не буду рахувати.
На завершення варто ще зауважити, що…
Примітка щодо підстановок Ейлера
Маючи інтеграл:
 ,
,
де:
- I тип, коли a>0
- II тип, коли c>0
- III тип, коли є два різні корені
очевидно, що часто можна буде його розв’язувати однією з двох підстановок Ейлера, або навіть будь-якою з них (коли a>0, c>0 і одночасно  ).
).
Жодних проблем, хоча з огляду на простоту обчислень я рекомендував би спочатку використовувати I тип, якщо це не вийде, то II, а якщо це також не вийде, то нарешті III.
Ось і все про використання підстановок Ейлера, сподіваюся, це стане вам у нагоді під час навчання, і як завжди, запрошую до коментарів під постом.