Маємо межу функції:
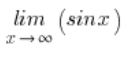
Інтуїтивно ми відчуваємо, що зазначена межа не існує. Значення x стають все більшими і більшими, а значення синуса “коливаються” весь час між -1 і 1.
Формальний доказ
Але як це формально довести?
З визначення межі функції при x, що прямує до нескінченності ми знаємо, що межа існує, якщо для кожної послідовності аргументів функції, що прямують до 
, відповідна їм послідовність значень функції збігається до одного і того ж числа (тоді це число і є межею).
Щоб показати, що така межа не існує, достатньо взяти дві будь-які послідовності аргументів, що прямують до і показати, що відповідні послідовності значень збігаються до двох різних чисел.
Ми знаємо, що функція синуса є періодичною, тому це можуть бути, наприклад, послідовності:
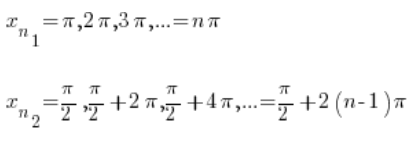
Очевидно, що обидві послідовності прямують до нескінченності при 
.
Тепер подивимося на відповідні цим послідовностям послідовності значень функції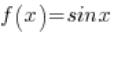 
:
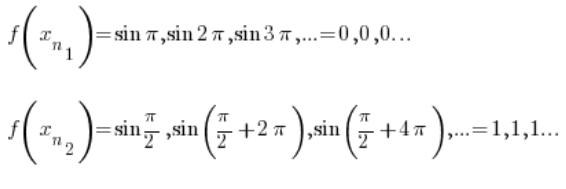
Очевидно, що перша послідовність збігається до 0, а друга – до 1.
Цього достатньо, щоб довести, що межа функції:
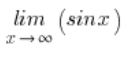
не існує.
