Немає товарів у кошику.
Krystian Karczyński- 3 Серпня 2024
- Komentarz 0
Неперервність функції в точці
Як ми всі знаємо (принаймні з мого курсу з меж), функція 
неперервна в точці 
, коли:
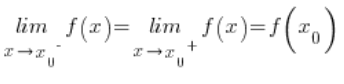
Тобто коли лівостороння межа цієї функції в цій точці дорівнює правосторонній межі функції в цій точці і дорівнює значенню функції в цій точці.
Якщо якась із цих рівностей не виконується, функція неперервна в точці , а точка називається точкою розриву.
У цій назві можна піти далі та розрізнити типи точок розриву. Ми робимо це так:
Точки розриву I типу
Точку називаємо точкою розриву I типу, якщо межі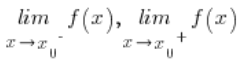 
кінцеві (тобто просто числа).
Крім того, якщо ці межі рівні між собою, тоді точка розриву I типу називається усувною.
Точки розриву II типу
Точку називаємо точкою розриву II типу, якщо якась із меж 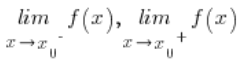не є кінцевою (тобто просто дорівнює плюс або мінус нескінченності).
Приклад 1
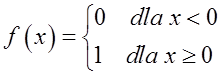
Ця функція має в точці 
точку розриву (тому що лівостороння межа в цій точці дорівнює 0, а правостороння межа 1). Це точка розриву I типу, тому що лівосторонні та правосторонні межі в цій точці є кінцевими (0 і 1). Це не усувна точка розриву I типу, тому що межі не рівні між собою.
Приклад 2
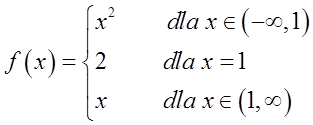
Ця функція має в точці 
точку розриву (тому що лівосторонні та правосторонні межі в цій точці не рівні значенню функції в цій точці). Це точка розриву I типу, тому що лівостороння та правостороння межі є кінцевими (і рівні 1). Це усувна точка розриву I типу, тому що лівостороння та правостороння межі рівні між собою.
Приклад 3
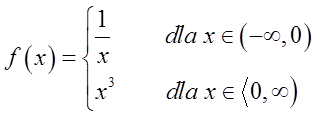
Ця функція має в точці точку розриву (тому що лівосторонні та правосторонні межі в цій точці не рівні між собою). Це точка розриву II типу, тому що лівостороння межа в цій точці дорівнює 
.
