Немає товарів у кошику.
Krystian Karczyński- 18 Червня 2024
- Komentarz 0
Для гранич багатьох послідовностей з логарифмами сміливо можна застосовувати перетворення і формули для логарифмів, відомі зі школи. Наприклад:
Приклад на границю послідовності з логарифмами
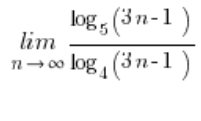
У ситуаціях, коли в логарифмах були різні основи і з цим нічого не можна було зробити, їх зводили до однієї основи за формулою: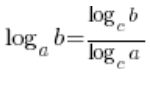 
. У нашій границі зручно буде взяти цю основу: 
. Маємо границю послідовності:
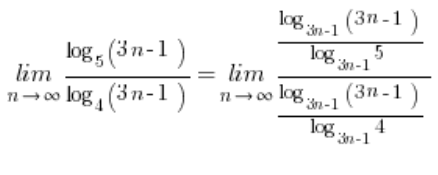
Знаємо, що 
, тобто у нашому виразі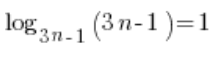 
. Отже:
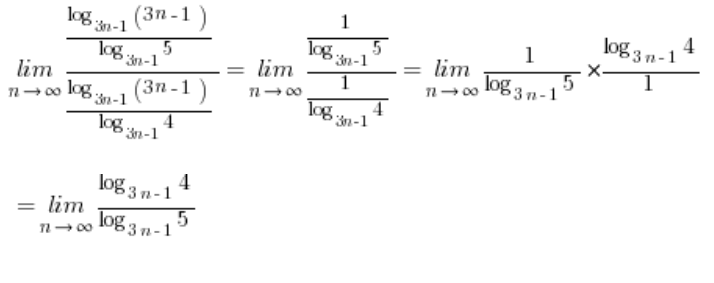
А цей вираз, скориставшись знову шкільною формулою (але цього разу у зворотному напрямку), буде дорівнювати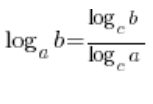 
…
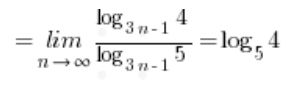
Що, звичайно, є результатом (ірраціональне число).
Навіть не було потреби застосовувати якісь методи на границі – вистачило шкільних перетворень логарифмів.
Хочеш дізнатися більше про обчислення границь? Рекомендую свій курс 🙂
