Еліптичні координати (подвійні інтеграли)
Krystian Karczyński
Засновник та керівник сервісу eTrapez.
Магістр математики Познанської Політехніки (Польща). Репетитор з математики з багаторічним досвідом. Творець перших Курсів eTrapez, які здобули величезну популярність серед студентів у всій Польщі.
Живе у Щецині (Польща). Любить прогулянки лісом, відпочинок на пляжі та каякінг.
Бувають у житті такі ситуації, коли областю інтегрування в подвійній інтегралі є еліпс….
Що тоді робити?
Еліптичні координати
Елегантним методом вирішення часто є використання так званих еліптичних координат. Це щось на кшталт полярних координат, механізм дії дуже схожий, лише ви підставляєте різні речі для x та y і якобіан інший. Інтерпретація ‘r’ також інша. Отже, підсумовуючи, якщо ви вмієте переходити до полярних координат (а це зазвичай робиться, коли областю інтегрування є коло), то ви без труднощів зрозумієте еліптичні координати.
Отже, ми маємо інтеграл: 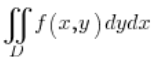 і область інтегрування, обмежену еліпсом з центром у початку координат, рівняння якого:
і область інтегрування, обмежену еліпсом з центром у початку координат, рівняння якого: 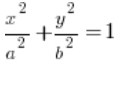 . Давайте впевнимось, що справа від рівняння еліпса точно 1, добре? Якщо, наприклад, там 9, можна легко зробити 1, поділивши обидві частини рівняння на 9.
. Давайте впевнимось, що справа від рівняння еліпса точно 1, добре? Якщо, наприклад, там 9, можна легко зробити 1, поділивши обидві частини рівняння на 9.
Область інтегрування, що малюється, виглядає так:
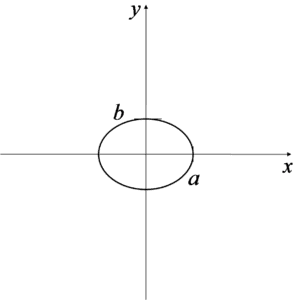
Що означають a і b, кожен бачить на рисунку. Потрібно бути уважним, бо якщо в знаменнику рівняння еліпса під ![]() є, наприклад, 9, то це означає, що
є, наприклад, 9, то це означає, що ![]() , очевидно чому, правда?
, очевидно чому, правда?
Отже, маючи таку “чисту” ситуацію, переходимо до еліптичних координат, підставляючи:
![]()
![]()
Значення змінних в еліптичних координатах
Кут ![]() означає те ж саме, що і в полярних координатах, а
означає те ж саме, що і в полярних координатах, а ![]() означає інше. У основних задачах з еліпсом, заданим гарним рівнянням
означає інше. У основних задачах з еліпсом, заданим гарним рівнянням 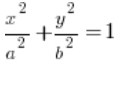 , просто припустимо, що
, просто припустимо, що ![]() змінюється від нуля до одного (у складніших випадках підставте
змінюється від нуля до одного (у складніших випадках підставте ![]() і
і ![]() у рівняння еліпса і обчисліть верхнє обмеження r).
у рівняння еліпса і обчисліть верхнє обмеження r).
Якобіан
Якобіан в еліптичних координатах дорівнює ![]() .
.
Запам’ятавши якобіан, переходимо до інтегралу в еліптичних координатах:
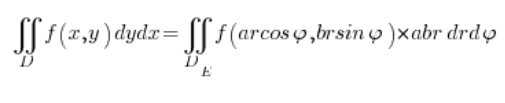
де змінні ![]() та
та ![]() обмежені:
обмежені: ![]() у межах від нуля до одного, а
у межах від нуля до одного, а ![]() залежно від того, говоримо ми про весь еліпс, половину чи, наприклад, чверть – як у полярних координатах.
залежно від того, говоримо ми про весь еліпс, половину чи, наприклад, чверть – як у полярних координатах.
Просто візьміть і рахуйте.
Приклад
Обчисліть інтеграл 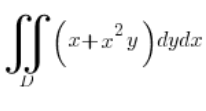 , де D – це еліпс з рівнянням:
, де D – це еліпс з рівнянням: 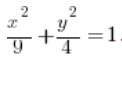 .
.
Згідно з наведеним вище планом, підставляємо:
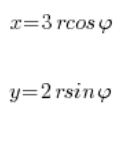
Беремо область інтегрування:
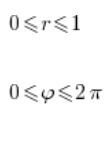
І рахуємо інтеграл:
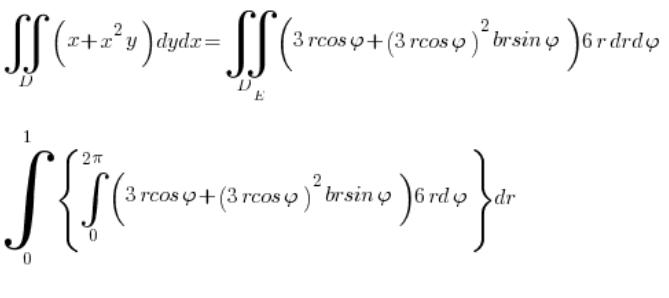
Що вже, звісно, є формальністю 🙂
Шукаєте репетитора з математики для університетського рівня або школи? А може вам потрібен курс, який підготує вас до вступних іспитів?
Ми - команда eTrapez. Ми вчимо математику ясно, просто і дуже детально - дістанемося навіть до найбільш відсторонених від знань.
Ми створили курси відео зрозумілою мовою для завантаження на комп'ютер, планшет або телефон. Вмикайте запис, дивіться і слухайте, як на репетиторстві. У будь-який час дня та ночі.