Визначені інтеграли, обчислені відносно змінної y

Визначені інтеграли можна обчислювати відносно змінної x або y, і іноді це навіть доцільно, якщо це зручніше. Це часто відіграє велику роль у застосуваннях інтегралів, таких як: обчислення площ ділянок, довжини дуг, об’єми та площі поверхонь обертових тіл. Часто у нас навіть немає вибору, адже умови завдання визначають, що крива обертається навколо осі OY, а не OX.

Як це зробити?

Перш за все, тобі потрібно зробити малюнок і позначити на ньому площу/довжину дуги/об’єм, які потрібно обчислити. Без цього не можна почати.

Друге, потрібно визначити межі інтегрування на осі OY (аналогічно, як це робиться на осі OX).

Тепер все, що вам потрібно зробити, це визначити обмежувальні криві для даних (зазвичай) стосовно змінної x за допомогою змінної y, наприклад, якщо ми маємо криву , ми визначаємо “x” і таким чином отримуємо дві функції змінної y: 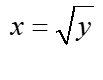і .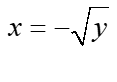

Потім ми просто створюємо відповідний інтеграл з межами інтегрування на осі OY та функціями змінної y, наприклад, у області площі це було б:

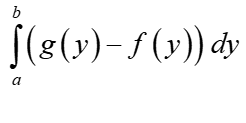
Я знову повторю, основа – це чіткий, великий графік!

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Related Posts

Ранг матриці, оцінений “на око”

Posted on 21 Червня 2024

Доведення того, що sin(x) не досягає межі при x, що прямує до нескінченності

Posted on 24 Червня 2024

Символ 0 у межах функцій та послідовностей

Posted on 27 Червня 2024