Tag: matura 2023 zmiany matematyka

Zmiany na maturze 2023 i 2024 – NOWA formuła 2023 – co pominąć ucząc się z Kursów Maturalnych eTrapez
Anna Zalewska
Absolwentka matematyki na Politechnice Śląskiej.
Korepetytor z 12-letnim doświadczeniem. Trener i wykładowca na Uniwersytecie Śląskim Maturzystów przy Uniwersytecie Śląskim w Katowicach. Certyfikowany nauczyciel MathRiders.
Mieszka w Chorzowie. Jest ratownikiem wodnym i członkiem Zarządu Oddziału Miejskiego WOPR. Lubi piec ciasta, ciasteczka, torty i przygotowywać różne słodkości.
W latach 2023 i 2024, czyli pierwsze dwa lata po wprowadzeniu matur w “nowej” formule egzamin będzie przebiegał nieco inaczej. Z racji na to, że przez jakiś czas uczniowie przebywali na nauce zdalnej, CKE wprowadziło pewne ograniczenia i ułatwienia.
Jednym z nich jest okrojenie materiału do nauki. Podstawa programowa została pomniejszona o wybrane treści. Więcej na ten temat poczytasz tutaj:
![]()
![]() ZMIANY NA MATURZE 2023 oraz 2024 (nowa formuła 2023)
ZMIANY NA MATURZE 2023 oraz 2024 (nowa formuła 2023)
W odpowiedzi na pojawiacie się pytania: “Czy mam przerabiać Pani cały Kurs maturalny? Skoro część materiału jest okrojona?”
Otóż nie do końca… W moich Kursach ujęłam wszystko tak, by objąć cały materiał podstawy programowej oraz by służyły one uczniom na lata 🙂
Na tegoroczną maturę 2024 wymogi zostały nieco okrojone, podobnie jak rok i dwa lata temu. Przygotowałam więc dokładniejszą rozpiskę, które zadania z danych lekcji możesz wyjątkowo „pominąć” przygotowując się do tegorocznego egzaminu z matematyki w NOWEJ formule 2023
P.S. Co możesz pominąć ucząc się z Kursu w STAREJ formule 2015 znajdziesz TUTAJ!
Kurs Matura Podstawowa (Formuła 2023)
► Lekcja 2 – Wyrażenia algebraiczne:
—> Zadanie 6 (wzory skróconego z potęgą 3) – przeniesione na PR
—> Zadanie 10 (wzory skróconego z potęgą 3) – przeniesione na PR
—> Zadanie 19 (wzory skróconego z potęgą 3) – przeniesione na PR
—> Zadanie 23 (znajdowania pierwiastków całkowitych wielomianu o współczynnikach całkowitych) – zostaje na PR
—> Zadanie 26 (wzory skróconego z potęgą 3) – przeniesione na PR
—> Zadanie 38 – 39 (wzory skróconego z potęgą 3) – przeniesione na PR
—> Zadanie 40 (wzory skróconego z potęgą n)
► Lekcja 3 – Równania i nierówności. Układy równań.:
—> Zadanie 1 (równanie dwukwadratowe)
—> Zadanie 21 (układów równań postaci 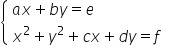 ) – przeniesione na PR
) – przeniesione na PR
—> Zadanie 22 (równanie dwukwadratowe)
► Lekcja 4 – Funkcje:
—> Zadanie 19 (wykres funkcji 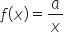 dla danego
dla danego 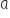 , korzystanie ze wzoru i wykresu tej funkcji do interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi)
, korzystanie ze wzoru i wykresu tej funkcji do interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi)
► Lekcja 5 – Ciągi:
—> Zadanie 6 (ciągi określone rekurencyjnie)
—> Zadanie 13 (ciągi określone rekurencyjnie)
► Lekcja 6 – Trygonometria:
—> Zadanie 11, 12 i 13 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
—> Zadanie 33 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
—> Zadanie 40 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
► Lekcja 7 – Planimetria:
—> Zadanie 36 (dowód geometryczny) – przeniesione na PR
—> Zadanie 38 (dowód geometryczny) – przeniesione na PR
—> Zadanie 39 (dowód geometryczny) – przeniesione na PR
► Lekcja 8 – Geometria analityczna:
—> Zadanie 5.2 (znajdowanie punktów wspólnych prostej i okręgu) – przeniesione na PR
—> Zadanie 6 (znajdowanie punktów wspólnych prostej i paraboli) – przeniesione na PR
—> Zadanie 11 (równanie prostej w postaci ogólnej) – przeniesione na PR
► Lekcja 9 – Stereometria:
—> Zadanie 9 (w ostrosłupach kąty między ścianami) – przeniesione na PR
—> Zadanie 11 (kąty w graniastosłupie) – przeniesione na PR
—> Zadanie 12 – 20 (bryły obrotowe: walec, stożek, kula)
—> Zadanie 22 (walec)
—> Zadanie 24 (walec)
—> Zadanie 25 (w ostrosłupach kąty między ścianami) – przeniesione na PR
—> Zadanie 26 – 27 (stożek)
—> Zadanie 31 (walec i stożek)
—> Zadanie 32 (stożek)
—> Zadanie 35 (w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami)
—> Zadanie 37 (walec)
—> Zadanie 40 (w ostrosłupach kąty między ścianami) – przeniesione na PR
Reasumując, zostały zadania dla poziomu PP: 1-8, 10, 21, 23, 28-30, 33-34, 36, 38-39. 🙂
Reasumując, zostały zadania dla poziomu PR: 1-11, 21, 23, 25, 28-30, 33-34, 36, 38-40. 🙂
► Lekcja 10 – Rachunek prawdopodobieństwa i statystyka:
—> Zadanie 8 (skala centylowa)
—> Zadanie 13.2 i 13.3 (wartość oczekiwaną, np. przy ustalaniu wysokości wygranej w prostych grach losowych i loteriach)
Kurs Matura Rozszerzona (Formuła 2023)
► Lekcja 2 – Wyrażenia algebraiczne:
—> Zadanie 11 (własności trójkąta Pascala oraz własności współczynnika dwumianowego (symbolu Newtona))
—> Zadanie 16 (własności współczynnika dwumianowego (symbolu Newtona))
► Lekcja 3 – Równania i nierówności:
—> Zadanie 13 (równania wielomianowe dające się łatwo sprowadzić do równań kwadratowych)
► Lekcja 4 – Rachunek prawdopodobieństwa i statystyka:
—> Zadanie 24 (wzór Bayesa)
► Lekcja 5 – Funkcje:
—> Zadanie 11 (funkcja homograficzna)
—> Zadanie 13 (funkcja homograficzna)
—> Zadanie 15 (dowodzenie monotoniczności funkcji zadanej wzorem w podanym przedziale)
—> Zadanie 24 (funkcja homograficzna)
► Lekcja 6 – Rachunek różniczkowy:
—> Zadanie 7 (własność Darboux)
—> Zadanie 26 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
—> Zadanie 30 (bryły obrotowe)
► Lekcja 7 – Ciągi:
—> Zadanie 6 (twierdzenie o trzech ciągach)
► Lekcja 10 – Geometria analityczna:
—> Zadanie 1 (znajdywanie punktów wspólnych dwóch okręgów)
—> Zadanie 6 (działania na wektorach)
► Lekcja 11 – Stereometria:
—> Zadanie 9 – 11 (bryły obrotowe)
—> Zadanie 13 (bryły obrotowe)
—> Zadanie 27 (bryły obrotowe)
—> Zadanie 29 (bryły obrotowe)
Kury Maturalne to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 40 zadaniami z podstawy i 30 zadaniami z rozszerzenia z KAŻDEGO działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu na nagraniu mamy 40 zadań z podstawy (lub 30 zadań z rozszerzenia) + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu podstawowego w nowej formule 2023 mają łącznie ponad 44h, z poziomu rozszerzonego ponad 43,5h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury.
Zachęcamy do zajrzenia na nasz kanał na YouTube i do playlisty z omówionymi Arkuszami maturalnymi z lat ubiegłych (CKE, Operon, Nowa Era).
Kursem, który tłumaczy wszystko „co i jak”, czyli tak podręcznikowo, od deski do deski, jest Kurs Funkcje KURS FUNKCJE Szkoła Średnia, KURS TRYGONOMETRIA oraz KURS PLANIMETRIA.
► KURS FUNKCJE Szkoła Średnia (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszamy także do drugiego tematycznego Kursu Trygonometria, gdzie omawiam pojęcia i zależności trygonometryczne jakie kryją się za trójkątami i kątami związane z sinusem, cosinusem, i tangensem.
► Kurs Trygonometria (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Kurs Planimetria jest multimedialnym kursem edukacyjnym dla uczniów szkół średnich, podzielonym na DWA odrębne Kursy. Omawiam w nim WSZYSTKIE zagadnienia na poziomie podstawowym jak i rozszerzonym. Przedstawione są tutaj szczegółowo: pojęcia wstępne, wektory, trójkąty, czworokąty, wielokąty, koła i okręgi oraz zadania z dowodami w planimetrii.
► Kurs Planimetria: Wprowadzenie, Trójkąty i Czworokąty
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.


Matura próbna CKE grudzień 2023. Test diagnostyczny z poziomu podstawowego. Matematyka. Nowa formuła 2023 (VIDEO+SCREENY)
Anna Zalewska
Absolwentka matematyki na Politechnice Śląskiej.
Korepetytor z 12-letnim doświadczeniem. Trener i wykładowca na Uniwersytecie Śląskim Maturzystów przy Uniwersytecie Śląskim w Katowicach. Certyfikowany nauczyciel MathRiders.
Mieszka w Chorzowie. Jest ratownikiem wodnym i członkiem Zarządu Oddziału Miejskiego WOPR. Lubi piec ciasta, ciasteczka, torty i przygotowywać różne słodkości.
W grudniu 2023 roku CKE przygotowało maturzystom matury próbne, w tym z matematyki na poziomie podstawowym. Uczniowie mieli okazję by znów sprawdzić swoje siły i wiedzę z “nowej” formuły.
Poniżej przedstawiam rozwiązania krok po kroku matury próbnej CKE grudzień 2023 z matematyki. Poziom PODSTAWOWY. Matura w NOWEJ formule 2023.
Zapraszam również do obejrzenia rozwiązań w formie graficznej, zamieszczonej na końcu wpisu.
Zapraszam oczywiście do rozwiązań innych matur, z CKE (majowych, dodatkowych z czerwca, poprawkowych oraz próbnych), a także matur próbnych z Operonu i Nowej Ery. Trochę się już ich nazbierało. 
Zapraszam na omówienie arkusza podstawowego z matury z matematyki Test Diagnostyczny grudzień 2023 w Nowej Formule.
SPIS TREŚCI:
0:00 – Wstęp
1:46 – Zadanie 1 zamknięte – 1p (potęgi: potęga ujemna, ułamkowa)
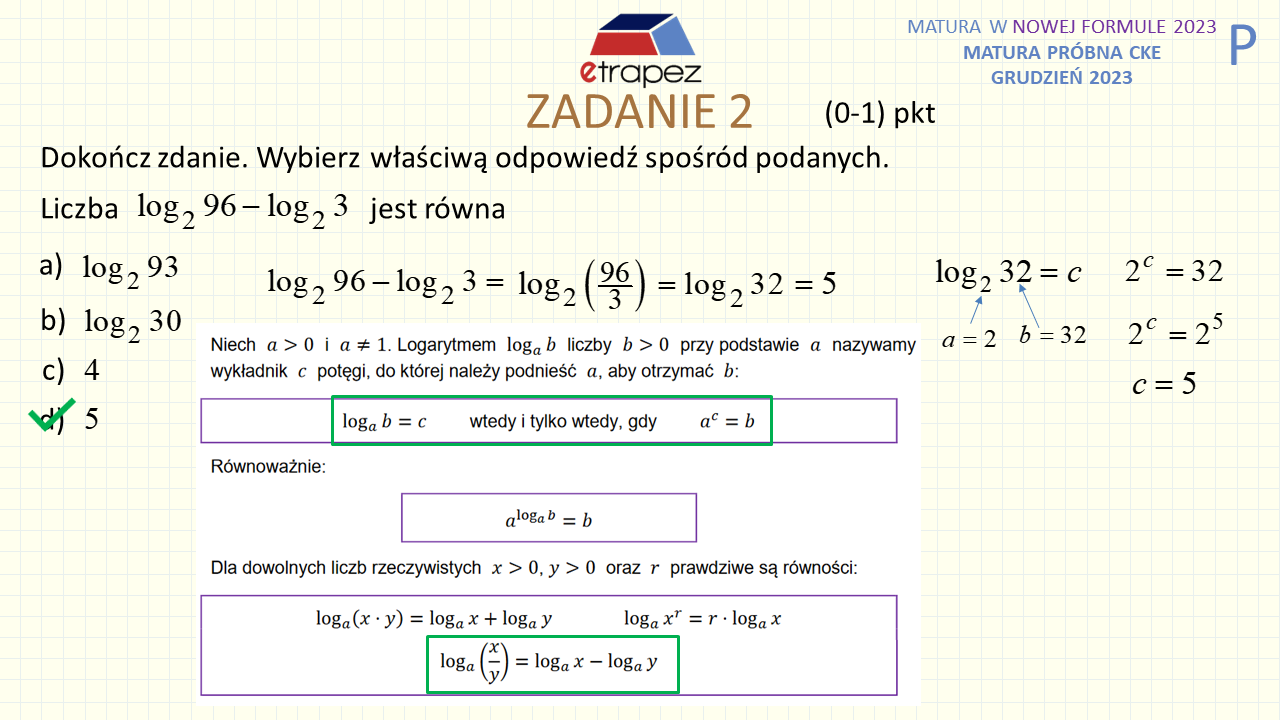
4:16 – Zadanie 2 zamknięte – 1p (logarytmy: odejmowanie dwóch logarytmów)
6:53 – Zadanie 3 zamknięte – 1p (lokata, procent składany)
9:34 – Zadanie 4 zamknięte – 1p (nierówność z wartością bezwzględną, oś liczbowa)
15:54 – Zadanie 5 otwarte – 2p (dowód algebraiczny: wykaż, że wyrażenie dla liczby nieparzystej jest podzielne przez 4)
19:48 – Zadanie 6 zamknięte – 1p (układ równań do rozwiązania)
22:49 – Zadanie 7 zamknięte – 1p (wyrażenie wymierne, sprowadzenie do jednego ułamka wyrażeń algebraicznych)
27:02 – Zadanie 8 zamknięte – 1p (wielomiany: podzielność przed dwumian)
30:23 – Zadanie 9 otwarte – 3p (równanie stopnia trzeciego, metoda grupowania)
34:11 – Zadanie 10 prawda-fałsz – 1p (funkcja liniowa: miejsce zerowe, przecięcie z osią OY)
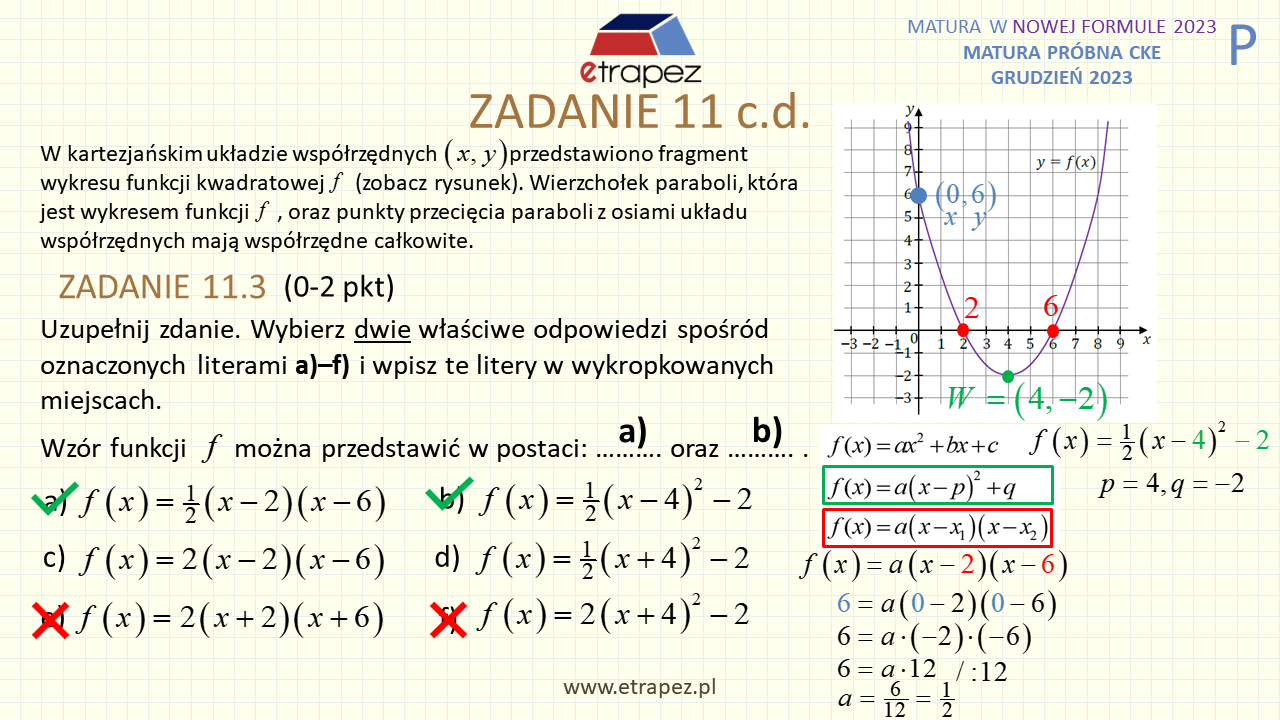
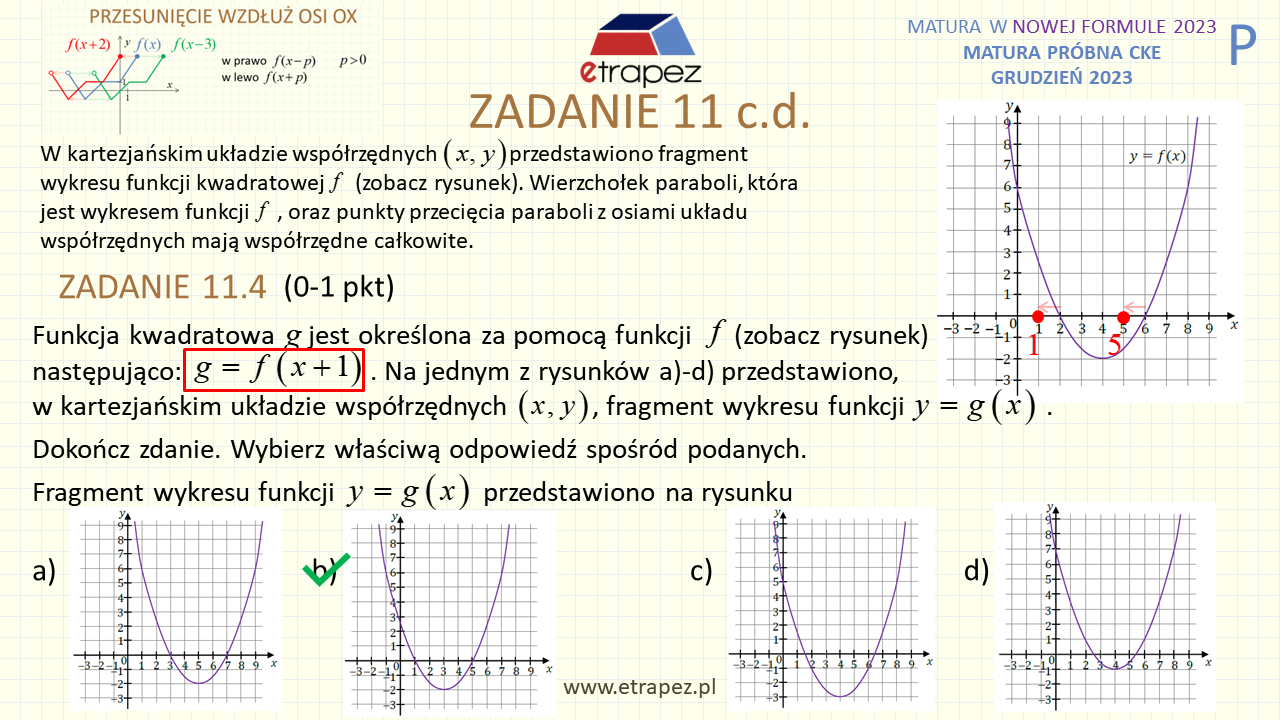
37:43 – Zadanie 11 wiązka zadań – 1+1+2+1p (funkcja kwadratowa: zbiór wartości, wartości ujemne, postać iloczynowa i kanoniczna, przesunięcie wykresu)
46:58 – Zadanie 12 zamknięte – 1p (zadanie z treścią, wartość funkcji w punkcie)
49:50 – Zadanie 13 zamknięte – 1p (ciąg arytmetyczny: podane dwa wyrazy, wyraz a6)
52:13 – Zadanie 14 prawda-fałsz – 1p (ciąg: podany wzór na sumę Sn, wartość wyrazu a1 i a2)
55:27 – Zadanie 15 zamknięte – 1p (ciąg geometryczny: trzy kolejne wyrazy)
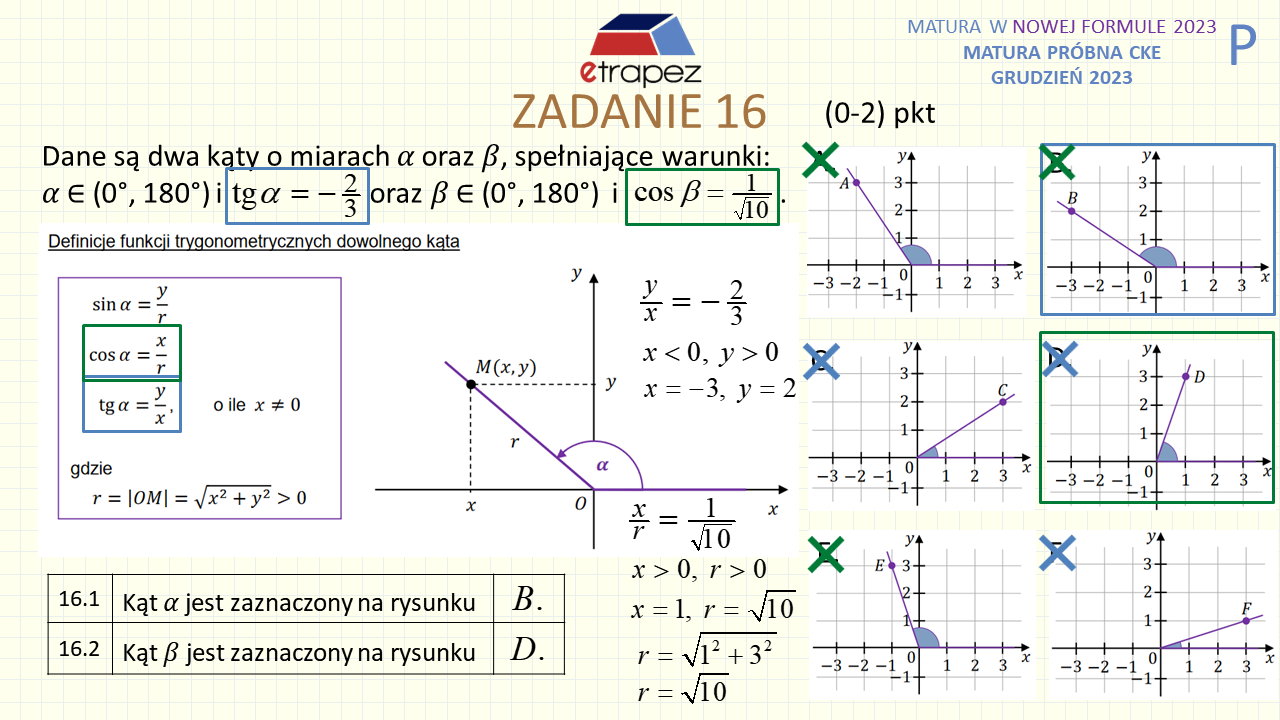
58:57 – Zadanie 16 zamknięte – 2p (trygonometria: tangens i cosinus, kąt w układzie współrzędnych)
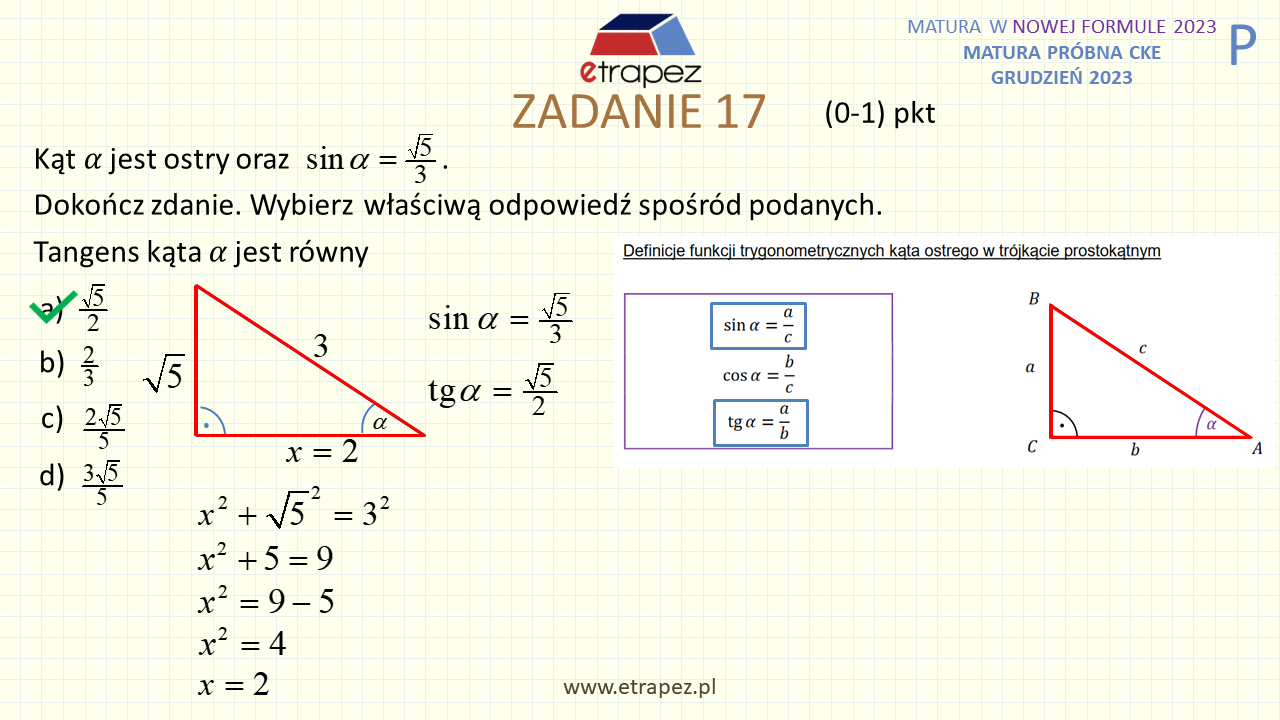
1:06:15 – Zadanie 17 zamknięte – 1p (trygonometria: podany sinus, wyznacz tangens)
1:09:15 – Zadanie 18 zamknięte – 1p (wzajemne położenie prostych, proste prostopadłe)
1:12:26 – Zadanie 19 zamknięte – 1p (wzajemne położenie prostych, proste równoległe)
1:14:44 – Zadanie 20 zamknięte – 1p (równanie okręgu)
1:18:19 – Zadanie 21 zamknięte – 1p (trójkąt równoboczny, podane 2 wierzchołki, długość odcinka, pole trójkąta)
1:22:15 – Zadanie 22 zamknięte – 1p (kąty w okręgu: kąty w trójkącie równoramiennym)
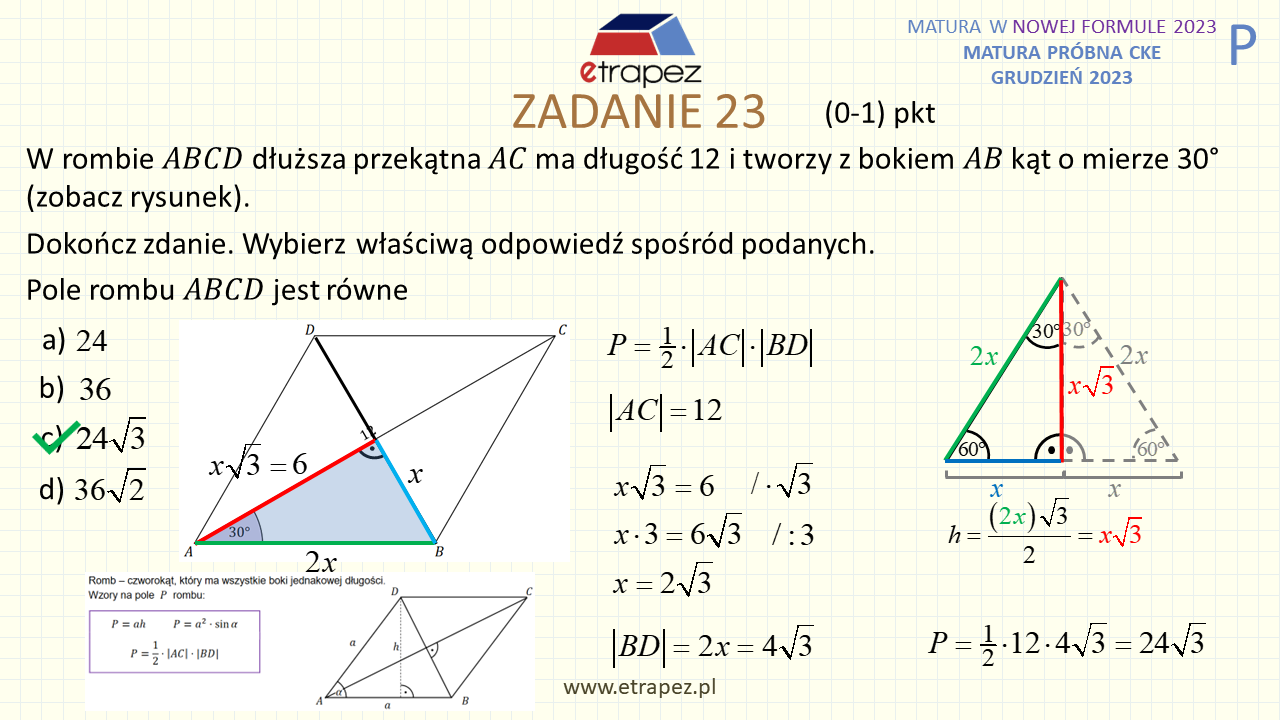
1:25:59 – Zadanie 23 zamknięte – 1p (romb: podany kąt i przekątna, pole rombu, trójkąt ekierkowy)
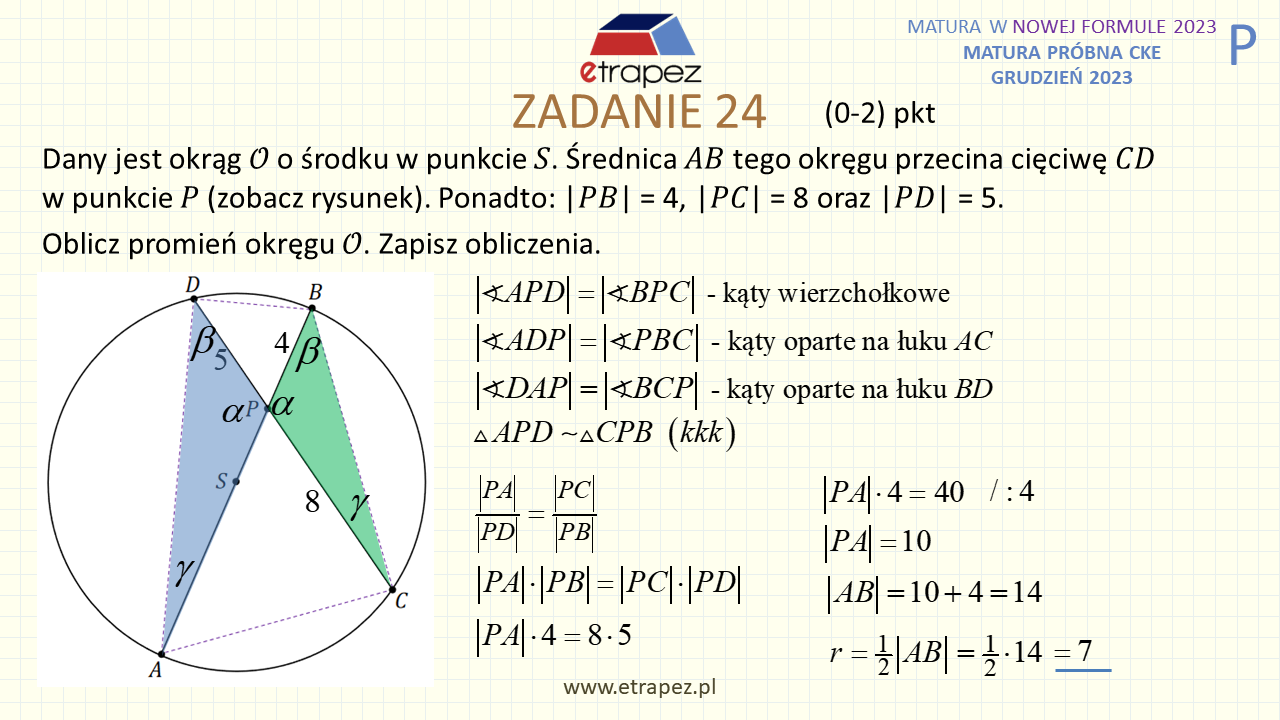
1:31:32 – Zadanie 24 otwarte – 2p (okrąg: odcinki w okręgu, trójkąty podobne, twierdzenie o cięciwach w okręgu)
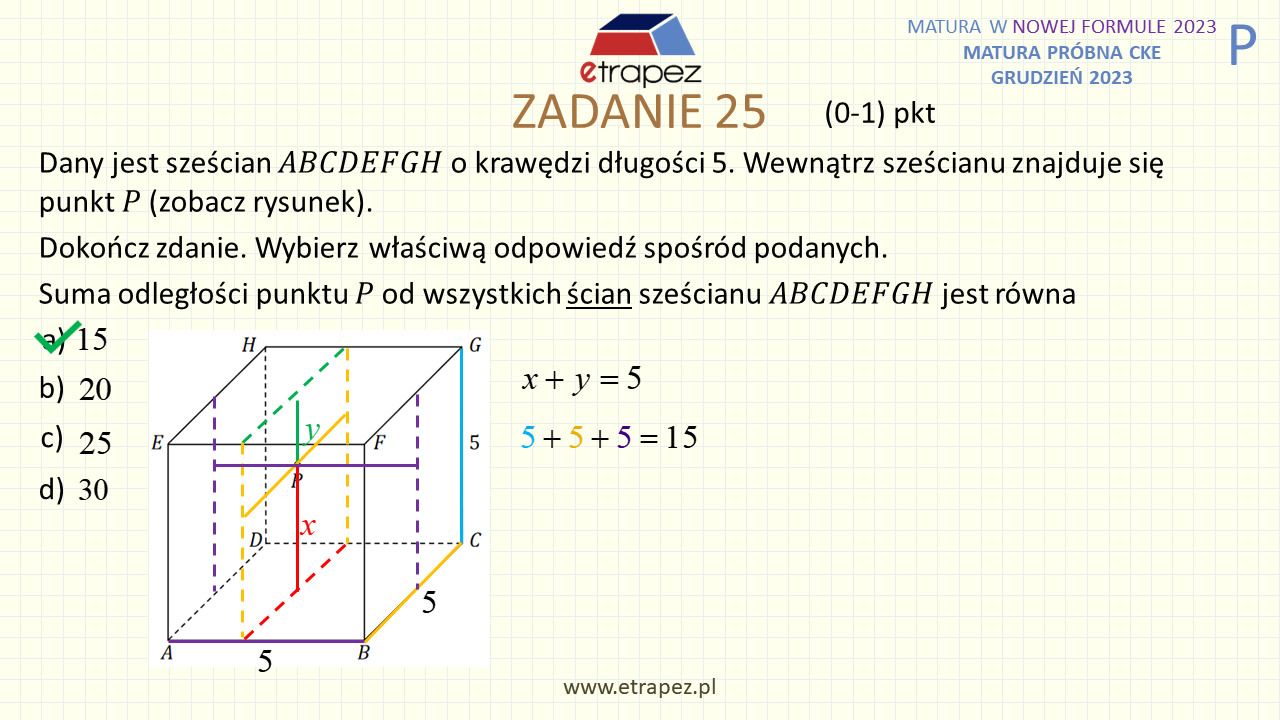
1:38:07 – Zadanie 25 zamknięte – 1p (sześcian: punkt wewnątrz figury, odległość od ścian)
1:41:48 – Zadanie 26 otwarte – 3p (ostrosłup prawidłowy czworokątny: podane objętość i kąt nachylenia ściany bocznej, wysokość ściany bocznej)
1:49:00 – Zadanie 27 otwarte – 2p (kombinatoryka: ile jest liczb sześciocyfrowych o różnych cyfrach, pierwsze trzy tworzą ciąg arytmetyczny)
1:54:06 – Zadanie 28 zamknięte – 1p (prawdopodobieństwo: rzut dwa razy kostką, iloczyn oczek jest nieparzysty)
1:56:19 – Zadanie 29 wiązka zadań – 1+1p (diagram słupkowy: prawdopodobieństwo, dominanta)
2:01:41 – Zadanie 30 otwarte – 4p (optymalizacja: funkcja kwadratowa, pole trapezu)
2:12:58 – Uwagi końcowe
Kurs MATURA PODSTAWOWA stanowi kompleksowe przygotowanie do matury podstawowej zarówno w “starej” formule 2015, jak i “nowej” formule 2023.
Sprawdź:
►Formuła 2023 oraz 2015: Kurs Matura Podstawowa
Ten Kurs Maturalny to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 40 zadaniami z danego działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu mamy 40 zadań na nagraniu + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu podstawowego w formule 2015 mają łącznie blisko 42h, w formule 2023 mają ponad 44h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury.
Zachęcamy do zajrzenia na nasz kanał i do playlisty z omówionymi Arkuszami maturalnymi (CKE, Operon, Nowa Era).
Kurs MATURA ROZSZERZONA stanowi kompleksowe przygotowanie do matury rozszerzonej zarówno w “starej” formule 2015, jak i “nowej” formule 2023.
Sprawdź:
►Formuła 2023 oraz 2015: Kurs Matura Rozszerzona
Ten Kurs Maturalny to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 30 zadaniami z danego działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu mamy 30 zadań na nagraniu + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu rozszerzonego w formule 2015 mają łącznie blisko 42,5h, w formule 2023 mają ponad 43,5h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury.
Zachęcamy do zajrzenia na nasz kanał i do playlisty z omówionymi Arkuszami maturalnymi (CKE, Operon, Nowa Era).
Kursem, który tłumaczy wszystko „co i jak”, czyli tak podręcznikowo, od deski do deski, jest KURS FUNKCJE Szkoła Średnia, KURS TRYGONOMETRIA oraz KURS PLANIMETRIA.
Kurs Funkcje omawia dokładnie wszystkie zagadnienia podstawowe funkcji (m.in. dziedzina, zbiór wartości, miejsca zerowe itp.), przesunięcia funkcji, funkcja liniowa, funkcja kwadratowa, wykładnicza, logarytmiczna oraz wymierna.
► Kurs Funkcje Szkoła Średnia (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszamy także do drugiego tematycznego Kursu Trygonometria, gdzie omawiam pojęcia i zależności trygonometryczne jakie kryją się za trójkątami i kątami związane z sinusem, cosinusem, i tangensem.
► Kurs Trygonometria (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszam również do Kursu Planimetria – omawiającego WSZYSTKIE zagadnienia na poziomie podstawowym jak i rozszerzonym. Przedstawione są tutaj szczegółowo: pojęcia wstępne, wektory, trójkąty, czworokąty, wielokąty, koła i okręgi oraz zadania z dowodami w planimetrii.
► Kurs Planimetria: Wprowadzenie, Trójkąty i Czworokąty
► Kurs Planimetria: Wielokąty, Okręgi i Dowody
Zapraszam również do obejrzenia rozwiązań w formie graficznej:
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.


Matura MAJ 2023. Poziom rozszerzony. NOWA FORMUŁA 2023 (VIDEO+SCREENY)
Anna Zalewska
Absolwentka matematyki na Politechnice Śląskiej.
Korepetytor z 12-letnim doświadczeniem. Trener i wykładowca na Uniwersytecie Śląskim Maturzystów przy Uniwersytecie Śląskim w Katowicach. Certyfikowany nauczyciel MathRiders.
Mieszka w Chorzowie. Jest ratownikiem wodnym i członkiem Zarządu Oddziału Miejskiego WOPR. Lubi piec ciasta, ciasteczka, torty i przygotowywać różne słodkości.
W tamtym roku szkolnym absolwenci liceum podeszli po raz pierwszy do matury w nowej formule 2023 (uczniowie kończący technikum podchodzili po raz ostatni jeszcze do “starej” formuły).
Poniżej przedstawiam rozwiązania krok po kroku matury CKE maj 2023 z matematyki. Poziom ROZSZERZONY. Matura w NOWEJ formule 2023.
Zapraszam również do obejrzenia rozwiązań w formie graficznej, zamieszczonej na końcu wpisu.
Zapraszam oczywiście do rozwiązań innych matur, z CKE (majowych, dodatkowych z czerwca oraz poprawkowych), a także matur próbnych z Operonu i Nowej Ery. Trochę się już ich nazbierało. 
Zapraszam na omówienie arkusza rozszerzonego z matury z matematyki maj 2023 w Nowej Formule.
SPIS TREŚCI:
0:00 – Wstęp
2:36 – Zadanie 1 – 2p (funkcja wykładnicza, rozpad substancji po t dobach)
8:00 – Zadanie 2 – 3p (prawdopodobieństwo: schemat Bernoullego)
15:53 – Zadanie 3 – 3p (styczna)
22:27 – Zadanie 4 – 3p (dowód algebraiczny: nierówność i równanie jednocześnie spełnione)
27:47 – Zadanie 5 – 3p (dowód geometryczny: trójkąt w trójkącie, zależności na bokach, twierdzenie sinusów)
37:31 – Zadanie 6 – 3p (równanie trygonometryczne)
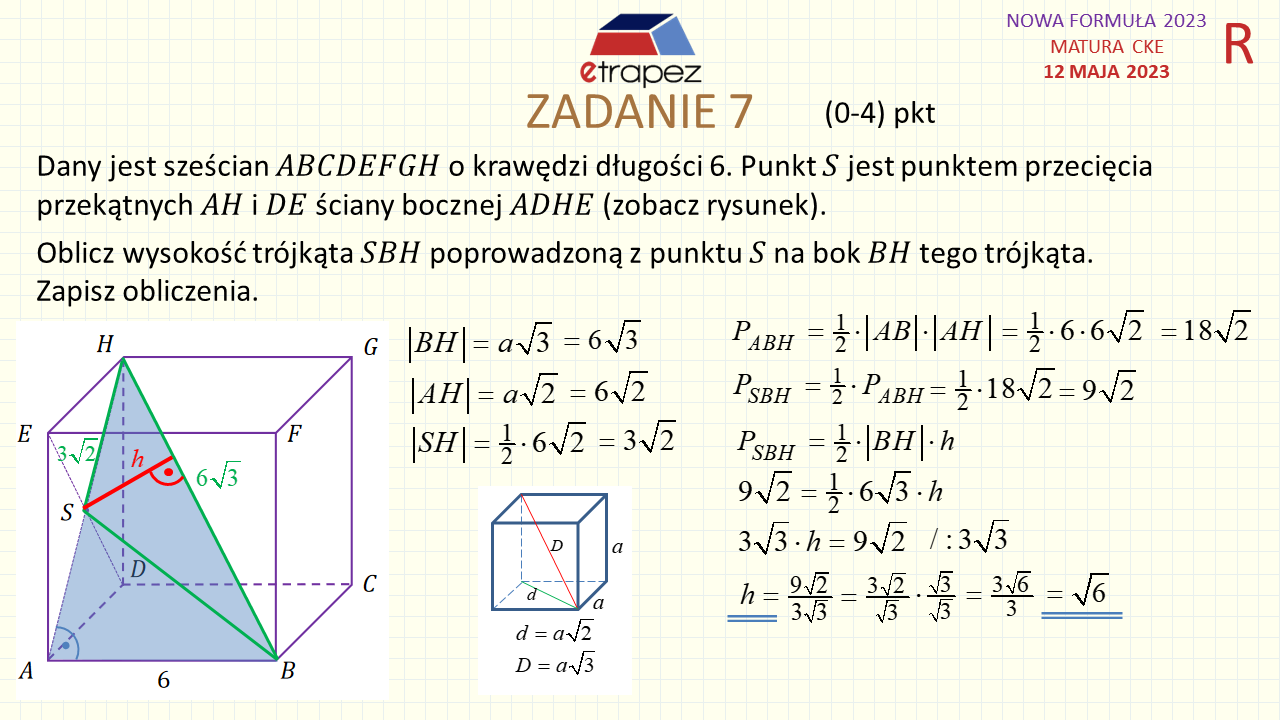
44:07 – Zadanie 7 – 4p (stereometria: sześcian, trójkąt wewnątrz bryły, wysokość)
51:23 – Zadanie 8 – 4p (planimetria: czworokąt opisany na okręgu, twierdzenie sinusów)
56:16 – Zadanie 9 – 4p (nierówność z modułami)
1:04:29 – Zadanie 10 – 4p (nieskończony ciąg geometryczny)
1:14:27 – Zadanie 11 – 5p (równanie kwadratowe z parametrem, wzory Viete’a)
1:23:20 – Zadanie 12.1 – 2p (logarytmy: logarytm w potędze, zamiana podstawy logarytmu)
1:30:23 – Zadanie 12.2 – 4p (optymalizacja: funkcja 4-go stopnia, wartość najmniejsza)
1:42:41 – Zadanie 13 – 6p (geometria analityczna: okrąg, parabola, trójkąt i cięciwa)
1:59:44 – Uwagi końcowe
A tu znajdziecie rozwiązania z poziomu PODSTAWOWEGO:
Matura MAJ 2023. Poziom PODSTAWOWY.
Kurs MATURA PODSTAWOWA stanowi kompleksowe przygotowanie do matury podstawowej zarówno w “starej” formule 2015, jak i “nowej” formule 2023.
Sprawdź:
►Formuła 2023 oraz 2015: Kurs Matura Podstawowa
Ten Kurs Maturalny to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 40 zadaniami z danego działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu mamy 40 zadań na nagraniu + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu podstawowego w formule 2015 mają łącznie blisko 42h, w formule 2023 mają ponad 44h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury.
Zachęcamy do zajrzenia na nasz kanał i do playlisty z omówionymi Arkuszami maturalnymi (CKE, Operon, Nowa Era).
Kurs MATURA ROZSZERZONA stanowi kompleksowe przygotowanie do matury rozszerzonej zarówno w “starej” formule 2015, jak i “nowej” formule 2023.
Sprawdź:
►Formuła 2023 oraz 2015: Kurs Matura Rozszerzona
Ten Kurs Maturalny to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 30 zadaniami z danego działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu mamy 30 zadań na nagraniu + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu rozszerzonego w formule 2015 mają łącznie blisko 42,5h, w formule 2023 mają ponad 43,5h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury.
Zachęcamy do zajrzenia na nasz kanał i do playlisty z omówionymi Arkuszami maturalnymi (CKE, Operon, Nowa Era).
Kursem, który tłumaczy wszystko „co i jak”, czyli tak podręcznikowo, od deski do deski, jest KURS FUNKCJE Szkoła Średnia, KURS TRYGONOMETRIA oraz KURS PLANIMETRIA.
Kurs Funkcje omawia dokładnie wszystkie zagadnienia podstawowe funkcji (m.in. dziedzina, zbiór wartości, miejsca zerowe itp.), przesunięcia funkcji, funkcja liniowa, funkcja kwadratowa, wykładnicza, logarytmiczna oraz wymierna.
► Kurs Funkcje Szkoła Średnia (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszamy także do drugiego tematycznego Kursu Trygonometria, gdzie omawiam pojęcia i zależności trygonometryczne jakie kryją się za trójkątami i kątami związane z sinusem, cosinusem, i tangensem.
► Kurs Trygonometria (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszam również do Kursu Planimetria – omawiającego WSZYSTKIE zagadnienia na poziomie podstawowym jak i rozszerzonym. Przedstawione są tutaj szczegółowo: pojęcia wstępne, wektory, trójkąty, czworokąty, wielokąty, koła i okręgi oraz zadania z dowodami w planimetrii.
► Kurs Planimetria: Wprowadzenie, Trójkąty i Czworokąty
► Kurs Planimetria: Wielokąty, Okręgi i Dowody
Zapraszam również do obejrzenia rozwiązań w formie graficznej:
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.


Matura MAJ 2023. Poziom podstawowy. NOWA FORMUŁA 2023 (VIDEO+SCREENY)
Anna Zalewska
Absolwentka matematyki na Politechnice Śląskiej.
Korepetytor z 12-letnim doświadczeniem. Trener i wykładowca na Uniwersytecie Śląskim Maturzystów przy Uniwersytecie Śląskim w Katowicach. Certyfikowany nauczyciel MathRiders.
Mieszka w Chorzowie. Jest ratownikiem wodnym i członkiem Zarządu Oddziału Miejskiego WOPR. Lubi piec ciasta, ciasteczka, torty i przygotowywać różne słodkości.
W tamtym roku szkolnym absolwenci liceum podeszli po raz pierwszy do matury w nowej formule 2023 (uczniowie kończący technikum podchodzili po raz ostatni jeszcze do “starej” formuły).
Poniżej przedstawiam rozwiązania krok po kroku matury CKE maj 2023 z matematyki. Poziom PODSTAWOWY. Matura w NOWEJ formule 2023.
Zapraszam również do obejrzenia rozwiązań w formie graficznej, zamieszczonej na końcu wpisu.
Zapraszam oczywiście do rozwiązań innych matur, z CKE (majowych, dodatkowych z czerwca oraz poprawkowych), a także matur próbnych z Operonu i Nowej Ery. Trochę się już ich nazbierało. 
Zapraszam na omówienie arkusza podstawowego z matury z matematyki maj 2023 w Nowej Formule.
SPIS TREŚCI:
0:00 – Wstęp
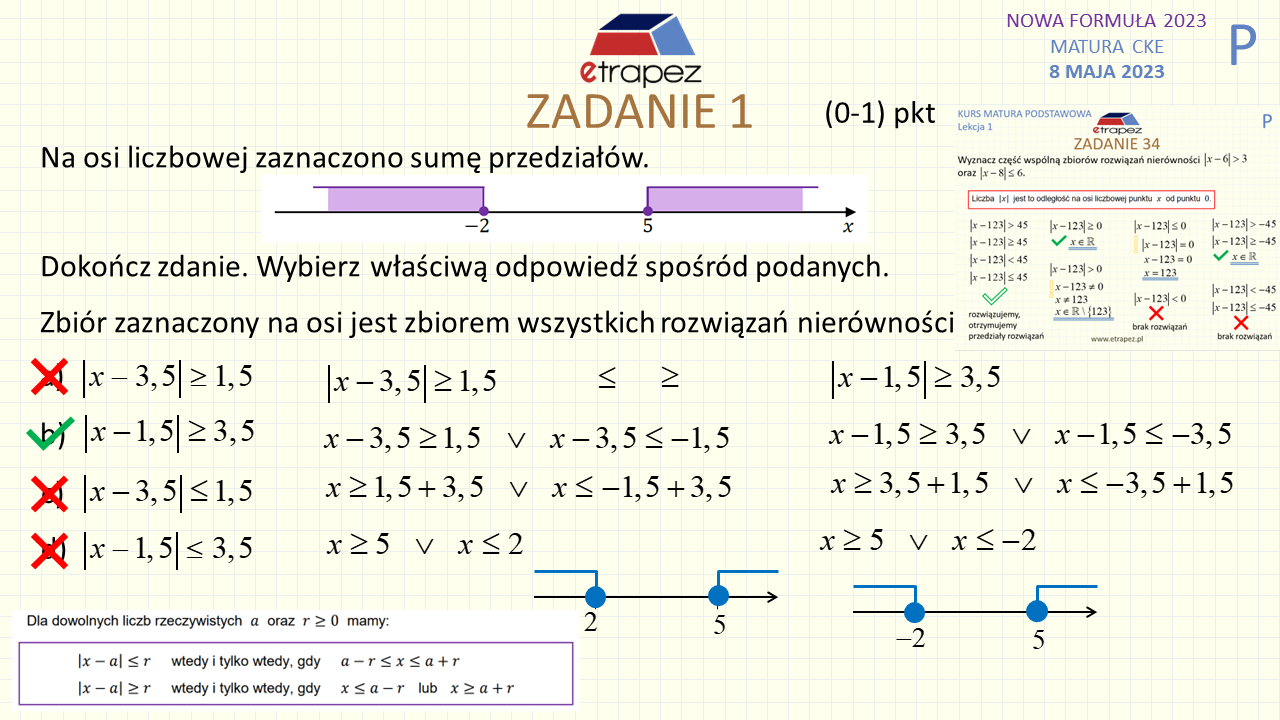
2:55 – Zadanie 1 zamknięte – 1p (nierówność z wartością bezwzględną, zbiór na osi liczbowej)
7:44 – Zadanie 2 zamknięte – 1p (pierwiastki 3-go stopnia)
9:28 – Zadanie 3 otwarte – 2p (dowód algebraiczny: wykaż, że wyrażenie jest podzielne przez 8)
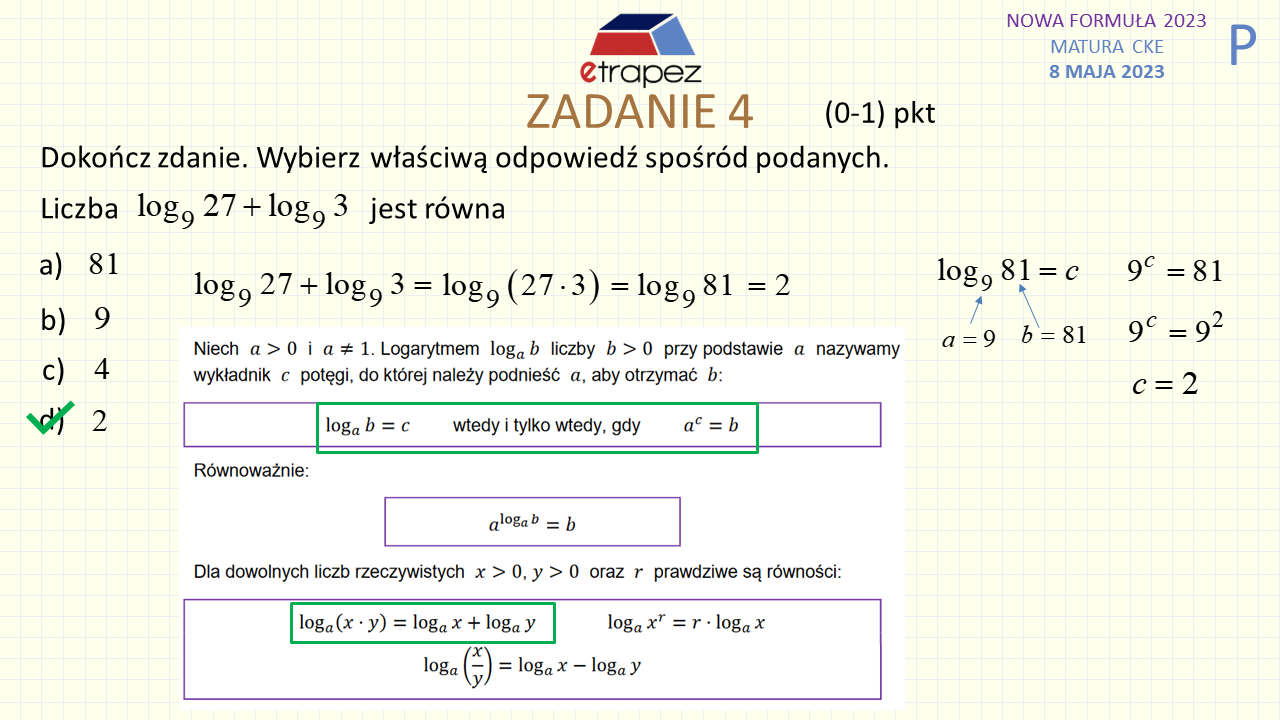
14:02 – Zadanie 4 zamknięte – 1p (logarytmy: dodawanie dwóch logarytmów)
16:02 – Zadanie 5 zamknięte – 1p (wzory skróconego mnożenia)
19:04 – Zadanie 6 zamknięte – 1p (nierówność)
21:15 – Zadanie 7 zamknięte – 1p (równanie w postaci iloczynu)
23:08 – Zadanie 8 zamknięte – 1p (równanie wymierne, pierwiastki, dziedzina ułamka)
27:14 – Zadanie 9 otwarte – 3p (równanie 3-go stopnia: grupowanie)
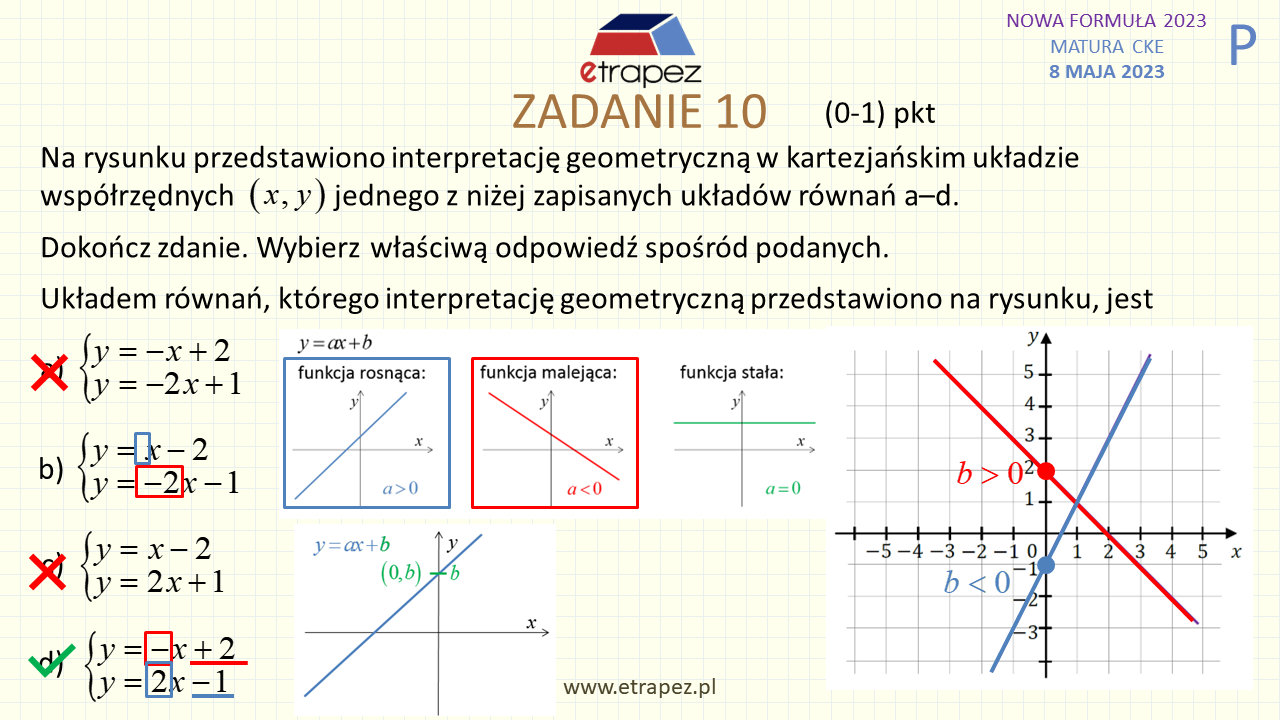
30:21 – Zadanie 10 zamknięte – 1p (układ równań: interpretacja graficzna, własności funkcji liniowej)
34:07 – Zadanie 11 zamknięte – 2p (układ równań: zadanie z treścią)
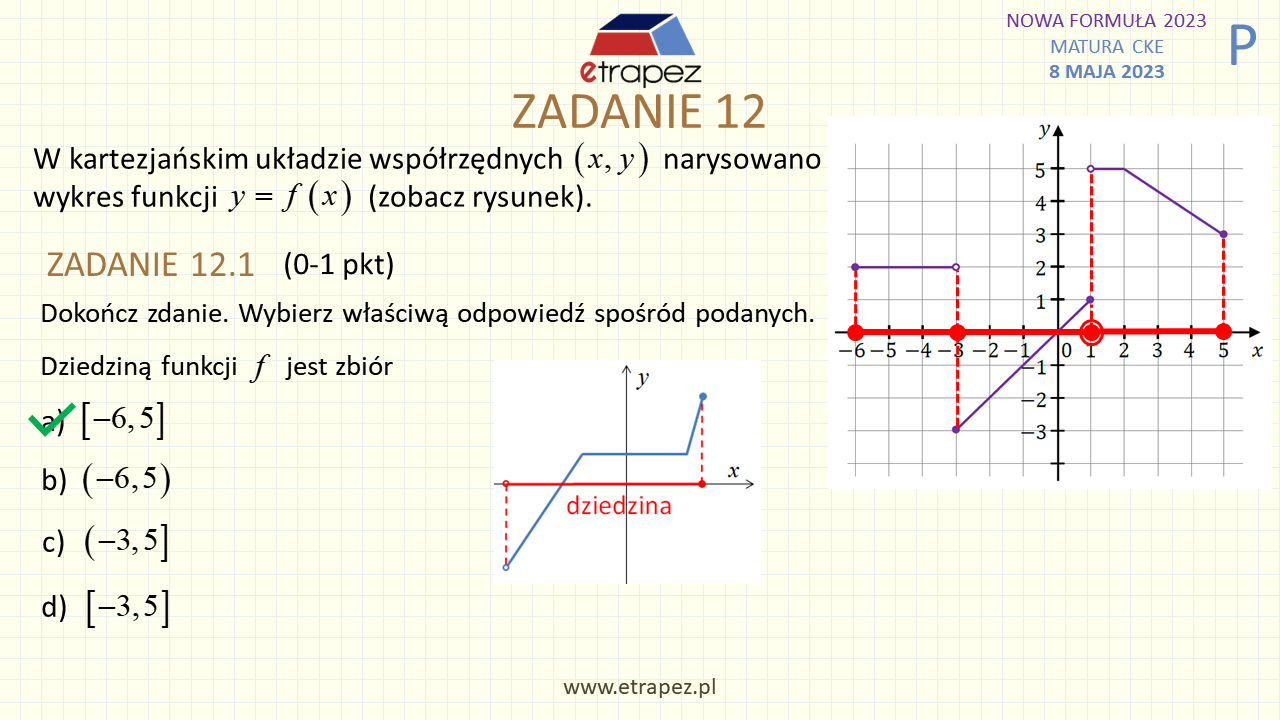
38:03 – Zadanie 12 wiązka zadań – 1+1+1p (funkcja: dziedzina, największa wartość w przedziale, monotoniczność)
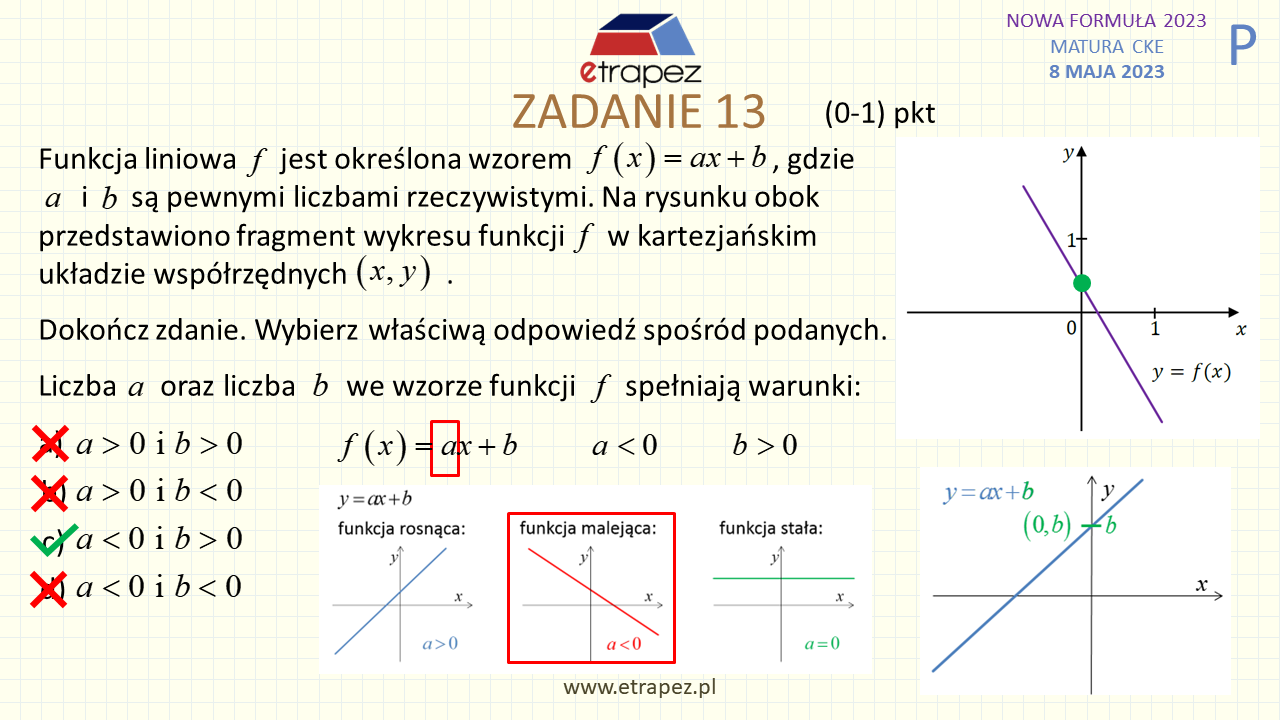
42:02 – Zadanie 13 zamknięte – 1p (funkcja liniowa: znaki współczynników)
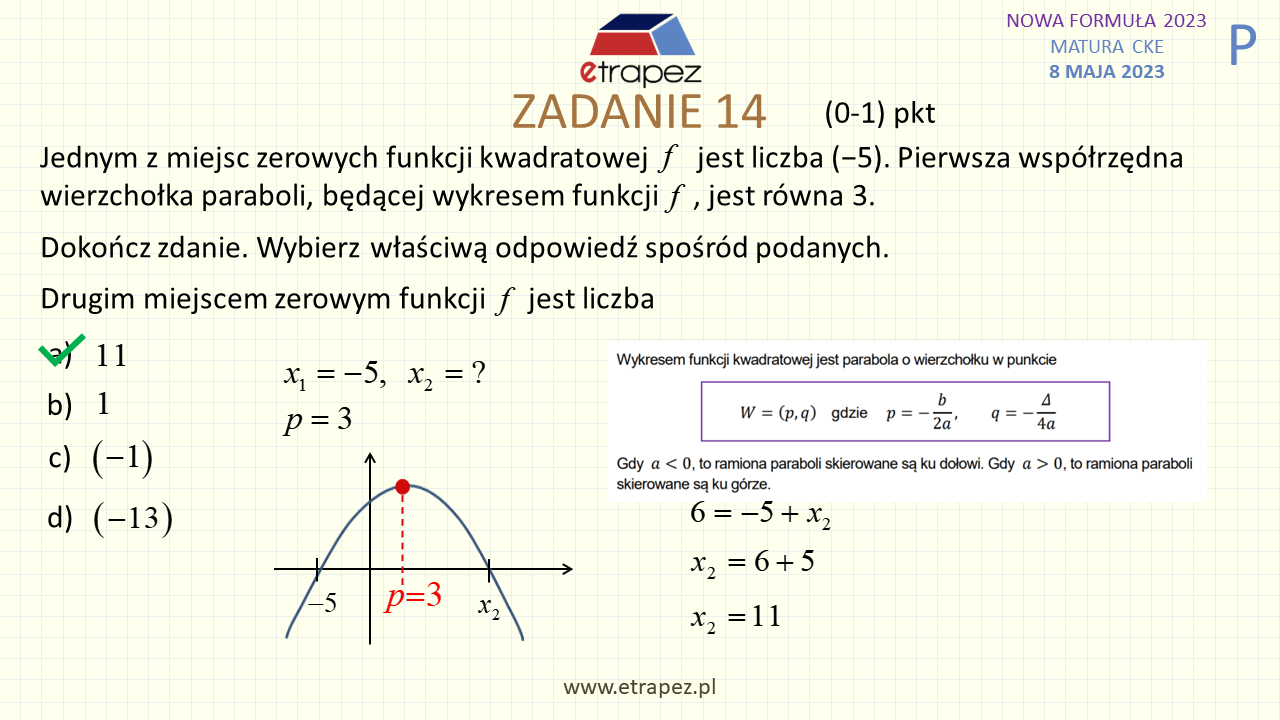
43:19 – Zadanie 14 zamknięte – 1p (funkcja kwadratowa: miejsca zerowe a “p” wierzchołka)
45:53 – Zadanie 15 zamknięte – 1p (ciąg: wyraz a4)
47:09 – Zadanie 16 zamknięte – 1p (ciąg geometryczny: trzy kolejne wyrazy)
49:26 – Zadanie 17 otwarte – 2p (ciąg arytmetyczny: suma, wyraz a1)
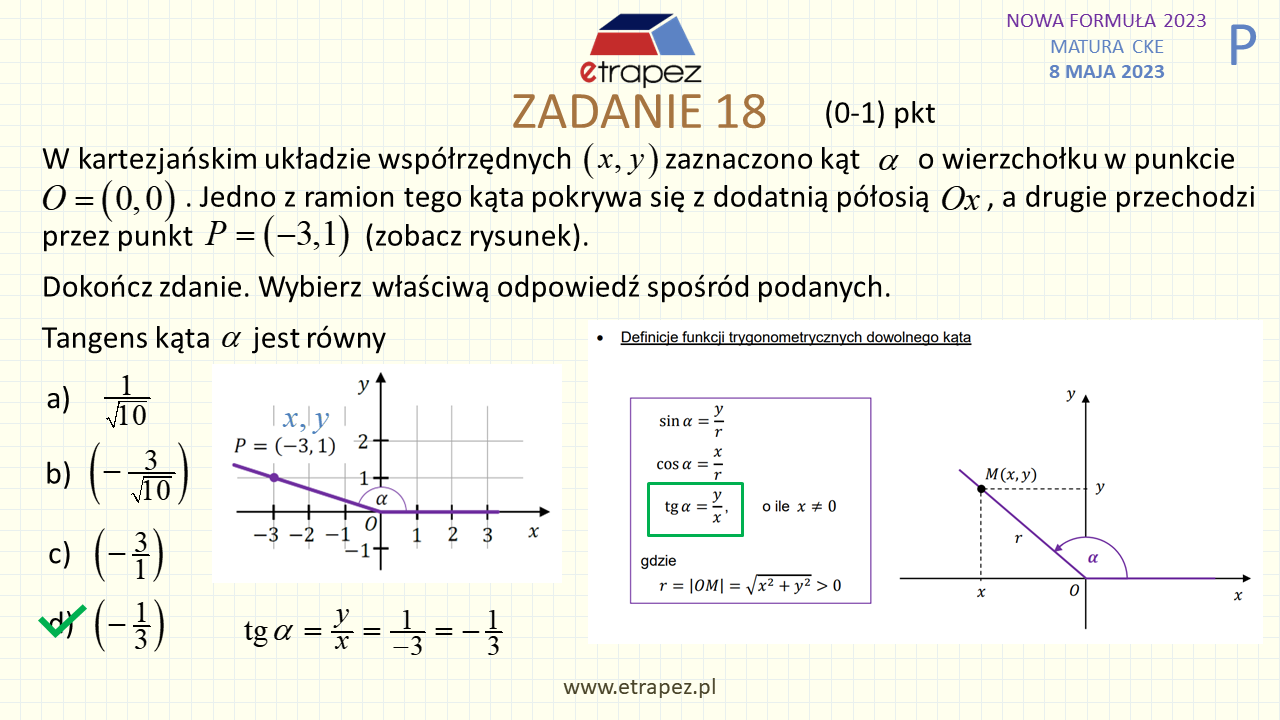
53:50 – Zadanie 18 zamknięte – 1p (trygonometria: tangens, kąt w układzie współrzędnych)
55:53 – Zadanie 19 zamknięte – 1p (trygonometria: wartość wyrażenia, jedynka trygonometryczna)
56:59 – Zadanie 20 zamknięte – 1p (romb: podany kąt i bok, iloczyn długości przekątnych)
1:00:19 – Zadanie 21 zamknięte – 1p (kąty w okręgu: kąt wpisany i środkowy, kąty w trójkącie równoramiennym)
1:02:26 – Zadanie 22 otwarte – 2p (trójkąty podobne, długość boku)
1:05:09 – Zadanie 23 z uzasadnieniem – 1p (proste prostopadłe)
1:09:33 – Zadanie 24 zamknięte – 1p (proste równoległe, prosta przechodząca przez punkt)
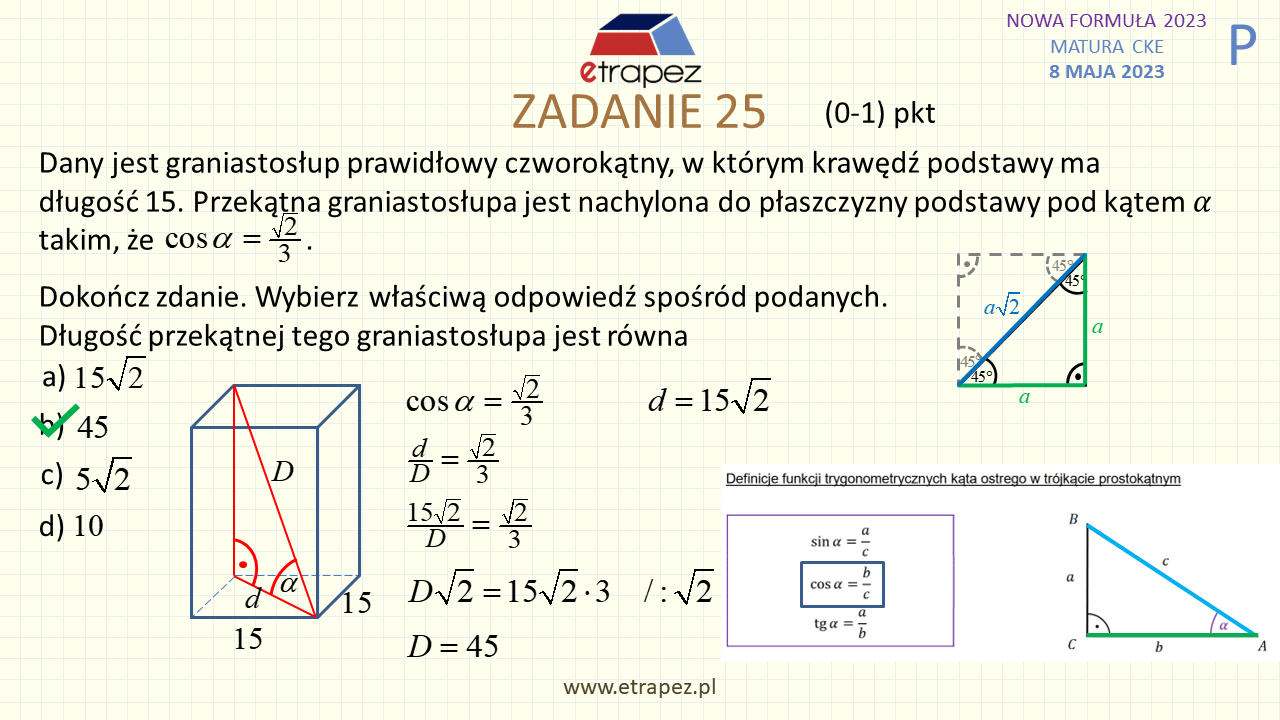
1:12:25 – Zadanie 25 zamknięte – 1p (graniastosłup: cosinus kąta między przekątną a podstawą, długość przekątnej)
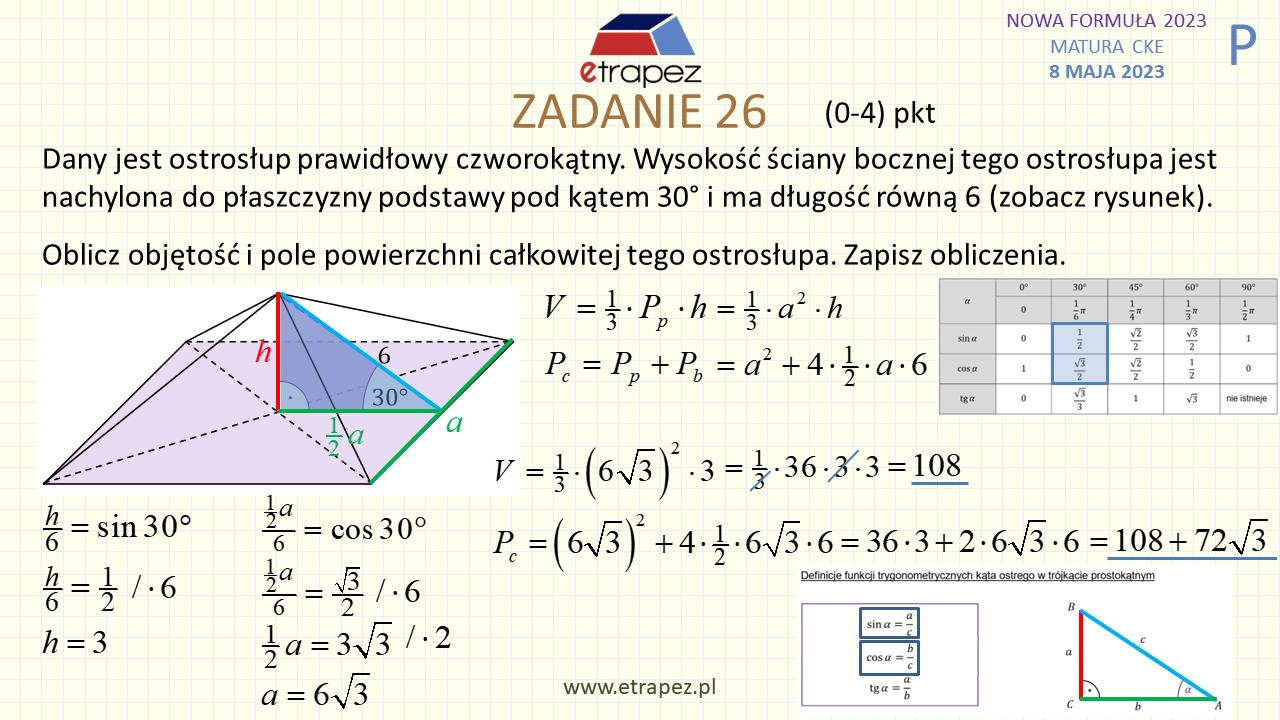
1:17:19 – Zadanie 26 otwarte – 4p (ostrosłup prawidłowy czworokątny: podane wysokość ściany bocznej i nachylenie do podstawy, objętość, pole całkowite)
1:23:52 – Zadanie 27 zamknięte – 1p (ostrosłup: liczba wierzchołków i krawędzi
1:28:54 – Zadanie 28 zamknięte – 1p (kombinatoryka: ile jest liczb pięciocyfrowych utworzonych z 0,5,7)
1:31:13 – Zadanie 29 zamknięte – 2p (mediana, średnia)
1:37:00 – Zadanie 30 otwarte – 2p (prawdopodobieństwo: losowanie dwóch liczb, ich iloczyn podzielny przez 15)
1:40:47 – Zadanie 31 wiązka zadań – 1+2p (optymalizacja: funkcja kwadratowa, wartość w punkcie, wartość maksymalna)
1:47:48 – Uwagi końcowe
A tu znajdziecie rozwiązania z poziomu ROZSZERZONEGO:
Matura MAJ 2023. Poziom Rozszerzony.
Kurs MATURA PODSTAWOWA stanowi kompleksowe przygotowanie do matury podstawowej zarówno w “starej” formule 2015, jak i “nowej” formule 2023.
Sprawdź:
►Formuła 2023 oraz 2015: Kurs Matura Podstawowa
Ten Kurs Maturalny to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 40 zadaniami z danego działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu mamy 40 zadań na nagraniu + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu podstawowego w formule 2015 mają łącznie blisko 42h, w formule 2023 mają ponad 44h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury.
Zachęcamy do zajrzenia na nasz kanał i do playlisty z omówionymi Arkuszami maturalnymi (CKE, Operon, Nowa Era).
Kurs MATURA ROZSZERZONA stanowi kompleksowe przygotowanie do matury rozszerzonej zarówno w “starej” formule 2015, jak i “nowej” formule 2023.
Sprawdź:
►Formuła 2023 oraz 2015: Kurs Matura Rozszerzona
Ten Kurs Maturalny to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 30 zadaniami z danego działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu mamy 30 zadań na nagraniu + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu rozszerzonego w formule 2015 mają łącznie blisko 42,5h, w formule 2023 mają ponad 43,5h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury.
Zachęcamy do zajrzenia na nasz kanał i do playlisty z omówionymi Arkuszami maturalnymi (CKE, Operon, Nowa Era).
Kursem, który tłumaczy wszystko „co i jak”, czyli tak podręcznikowo, od deski do deski, jest KURS FUNKCJE Szkoła Średnia, KURS TRYGONOMETRIA oraz KURS PLANIMETRIA.
Kurs Funkcje omawia dokładnie wszystkie zagadnienia podstawowe funkcji (m.in. dziedzina, zbiór wartości, miejsca zerowe itp.), przesunięcia funkcji, funkcja liniowa, funkcja kwadratowa, wykładnicza, logarytmiczna oraz wymierna.
► Kurs Funkcje Szkoła Średnia (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszamy także do drugiego tematycznego Kursu Trygonometria, gdzie omawiam pojęcia i zależności trygonometryczne jakie kryją się za trójkątami i kątami związane z sinusem, cosinusem, i tangensem.
► Kurs Trygonometria (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszam również do Kursu Planimetria – omawiającego WSZYSTKIE zagadnienia na poziomie podstawowym jak i rozszerzonym. Przedstawione są tutaj szczegółowo: pojęcia wstępne, wektory, trójkąty, czworokąty, wielokąty, koła i okręgi oraz zadania z dowodami w planimetrii.
► Kurs Planimetria: Wprowadzenie, Trójkąty i Czworokąty
► Kurs Planimetria: Wielokąty, Okręgi i Dowody
Zapraszam również do obejrzenia rozwiązań w formie graficznej:
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.


Zmiany na maturze 2023 i 2024 – STARA formuła 2015 – co pominąć ucząc się z Kursów Maturalnych eTrapez
Anna Zalewska
Absolwentka matematyki na Politechnice Śląskiej.
Korepetytor z 12-letnim doświadczeniem. Trener i wykładowca na Uniwersytecie Śląskim Maturzystów przy Uniwersytecie Śląskim w Katowicach. Certyfikowany nauczyciel MathRiders.
Mieszka w Chorzowie. Jest ratownikiem wodnym i członkiem Zarządu Oddziału Miejskiego WOPR. Lubi piec ciasta, ciasteczka, torty i przygotowywać różne słodkości.
Przez najbliższe dwa lata (2023 i 2024) egzamin maturalny będzie przebiegał nieco inaczej. Z racji na to, że przez jakiś czas uczniowie przebywali na nauce zdalnej, CKE wprowadziło pewne ograniczenia i ułatwienia.
Jednym z nich jest okrojenie materiału do nauki. Podstawa programowa została pomniejszona o wybrane treści. Więcej na ten temat poczytasz tutaj:
![]()
![]() ZMIANY NA MATURZE 2023 oraz 2024 (stara formuła 2015)
ZMIANY NA MATURZE 2023 oraz 2024 (stara formuła 2015)
W odpowiedzi na pojawiacie się pytania: “Czy mam przerabiać Pani cały Kurs maturalny? Skoro część materiału jest okrojona?”
Otóż nie do końca… W moich Kursach ujęłam wszystko tak, by objąć cały materiał podstawy programowej oraz by służyły one uczniom na lata 🙂
Na tegoroczną maturę 2023 wymogi zostały nieco okrojone, podobnie jak rok i dwa lata temu. Przygotowałam więc dokładniejszą rozpiskę, które zadania z danych lekcji możesz wyjątkowo „pominąć” przygotowując się do tegorocznego egzaminu z matematyki w STAREJ formule 2015
P.S. Co możesz pominąć ucząc się z Kursów w NOWEJ formule 2023 znajdziesz TUTAJ!
Kurs Matura Podstawowa (Formuła 2015)
► Lekcja 1 – Liczby Rzeczywiste:
—> Zadanie 10 (błąd bezwzględny i błąd względny przybliżenia)
—> Zadanie 34 (błąd bezwzględny i błąd względny przybliżenia)
► Lekcja 4 – Funkcje:
—> Zadanie 19 (wykres funkcji 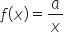 dla danego
dla danego 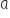 , korzystanie ze wzoru i wykresu tej funkcji do interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi)
, korzystanie ze wzoru i wykresu tej funkcji do interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi)
—> Zadanie 36 (wartość najmniejszą i wartość największą funkcji kwadratowej w przedziale domkniętym)
—> Zadanie 39 (funkcja wykładnicza)
► Lekcja 6 – Trygonometria:
—> Zadanie 10 (miara kąta ostrego, dla której funkcja trygonometryczna przyjmuje daną wartość, korzystanie z tablic lub kalkulatora – przybliżona)
—> Zadanie 11 (miara kąta ostrego, dla której funkcja trygonometryczna przyjmuje daną wartość, korzystanie z tablic lub kalkulatora – przybliżona)
—> Zadanie 13 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
—> Zadanie 17 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
—> Zadanie 19 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
—> Zadanie 20 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
—> Zadanie 39 (miara kąta ostrego, dla której funkcja trygonometryczna przyjmuje daną wartość, korzystanie z tablic lub kalkulatora – przybliżona)
—> Zadanie 40 (przybliżone wartości funkcji trygonometrycznych, odczytane z tablic lub obliczonych za pomocą kalkulatora)
► Lekcja 7 – Planimetria:
—> Zadanie 20 (własności okręgów stycznych)
—> Zadanie 34 (trójkąty podobne i wykorzystanie cechy ich podobieństwa w kontekstach praktycznych)
► Lekcja 9 – Stereometria:
—> Zadanie 8 (w ostrosłupach kąt między odcinkami i płaszczyznami (między krawędziami i ścianami))
—> Zadanie 9 (w ostrosłupach kąty między ścianami)
—> Zadanie 11 (walec)
—> Zadanie 12 (walec)
—> Zadanie 13 (walec, kąt między odcinkami oraz kąt między odcinkami i płaszczyznami)
—> Zadanie 14 (stożek)
—> Zadanie 15 (w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami)
—> Zadanie 16 (stożek)
—> Zadanie 17 (w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami)
—> Zadanie 18 (stożek)
—> Zadanie 19 (kula)
—> Zadanie 20 (kula)
—> Zadanie 22 (walec)
—> Zadanie 24 (walec)
—> Zadanie 25 (w ostrosłupach kąty między ścianami)
—> Zadanie 26 (w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami)
—> Zadanie 27 (stożek)
—> Zadanie 30 (w ostrosłupach kąt między odcinkami i płaszczyznami (między krawędziami i ścianami) oraz kąt między ścianami)
—> Zadanie 31 (walec i stożek)
—> Zadanie 32 (stożek)
—> Zadanie 35 (w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami)
—> Zadanie 37 (walec)
—> Zadanie 40 (w ostrosłupach kąty między ścianami)
Reasumując, zostały zadania: 1-7, 10, 21, 23, 28-29, 33-34, 36, 38-39.
► Lekcja 10 – Rachunek prawdopodobieństwa i statystyka:
—> Zadanie 15 (średnia ważona)
—> Zadanie 20 (odchylenie standardowe zestawu danych)
—> Zadanie 38 (średnia ważona)
—> Zadanie 40 (odchylenie standardowe zestawu danych)
Kurs Matura Rozszerzona (Formuła 2015)
► Lekcja 1 – Liczby Rzeczywiste:
—> Zadanie 9 (błąd bezwzględny i błąd względny przybliżenia)
► Lekcja 3 – Równania i nierówności:
—> Zadanie 10 (interpretacja graficzna układów nierówności liniowych z dwiema niewiadomymi)
—> Zadanie 13 (równania wielomianowe dające się łatwo sprowadzić do równań kwadratowych)
—> Zadanie 29 (interpretacja graficzna nierówności liniowej z dwiema niewiadomymi)
► Lekcja 4 – Rachunek prawdopodobieństwa i statystyka:
—> Zadanie 10 (odchylenie standardowe zestawu danych)
► Lekcja 5 – Funkcje:
—> Zadanie 2 (wartość najmniejszą i wartość największą funkcji kwadratowej w przedziale domkniętym)
—> Zadanie 9 (funkcja wykładnicza)
► Lekcja 7 – Ciągi:
—> Zadanie 4 i 5 (ciąg określony wzorem rekurencyjnym)
► Lekcja 8 – Trygonometria:
—> Zadanie 14 (nierówność trygonometryczna)
—> Zadanie 27, 28, 29 i 30 (nierówność trygonometryczna)
► Lekcja 10 – Geometria analityczna:
—> Zadanie 2 (równoległość i prostopadłość prostych na podstawie ich równań ogólnych)
—> Zadanie 8 (interpretacja graficzna nierówności liniowej z dwiema niewiadomymi)
—> Zadanie 10 (skala jednokładności)
—> Zadanie 24 (skala jednokładności)
► Lekcja 11 – Stereometria:
—> Zadanie 1 (w ostrosłupie kąty między odcinkami i kąty między odcinkami i płaszczyznami)
—> Zadanie 8 (w ostrosłupie kąty między odcinkami i kąty między odcinkami i płaszczyznami)
—> Zadanie 9 (w walcach i w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami)
—> Zadanie 11 (bryły obrotowe)
—> Zadanie 12 (w ostrosłupie kąty między odcinkami i płaszczyznami)
—> Zadanie 13 (bryły obrotowe)
—> Zadanie 14 (w ostrosłupie kąty między odcinkami i kąty między odcinkami i płaszczyznami)
—> Zadanie 20 (w ostrosłupie kąty między ścianami)
—> Zadanie 24, 25, 26 (w ostrosłupie kąty między odcinkami i kąty między odcinkami i płaszczyznami oraz między ścianami)
—> Zadanie 29 (bryły obrotowe)
Kury Maturalne to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 40 zadaniami z podstawy i 30 zadaniami z rozszerzenia z KAŻDEGO działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu na nagraniu mamy 40 zadań z podstawy (lub 30 zadań z rozszerzenia) + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu podstawowego w starej formule 2015 mają łącznie ponad 41,5h, z poziomu rozszerzonego około 42,5h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury.
Zachęcamy do zajrzenia na nasz kanał na YouTube i do playlisty z omówionymi Arkuszami maturalnymi z lat ubiegłych (CKE, Operon, Nowa Era).
Kursem, który tłumaczy wszystko „co i jak”, czyli tak podręcznikowo, od deski do deski, jest Kurs Funkcje KURS FUNKCJE Szkoła Średnia, KURS TRYGONOMETRIA oraz KURS PLANIMETRIA.
► KURS FUNKCJE Szkoła Średnia (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszamy także do drugiego tematycznego Kursu Trygonometria, gdzie omawiam pojęcia i zależności trygonometryczne jakie kryją się za trójkątami i kątami związane z sinusem, cosinusem, i tangensem.
► Kurs Trygonometria (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Kurs Planimetria jest multimedialnym kursem edukacyjnym dla uczniów szkół średnich, podzielonym na DWA odrębne Kursy. Omawiam w nim WSZYSTKIE zagadnienia na poziomie podstawowym jak i rozszerzonym. Przedstawione są tutaj szczegółowo: pojęcia wstępne, wektory, trójkąty, czworokąty, wielokąty, koła i okręgi oraz zadania z dowodami w planimetrii.
► Kurs Planimetria: Wprowadzenie, Trójkąty i Czworokąty
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.