Currently Empty: zł0.00

W tym roku, podobnie jak w 2021, uczniów czekają małe zmiany na egzaminie maturalnym. Z powodu pandemii koronawirusa COVID-19 oraz nietypowej sytuacji, jaką jest nauka zdalna w domu przez niemal cały rok szkolny, Ministerstwo Edukacji i Nauki wyszło na przeciw uczniom. Dnia 16 grudnia 2020 r. wydało rozporządzenie dokonujące pewnych zmian w egzaminie oraz w wymogach programowych do tego egzaminu.
Matematyka jako przedmiot obowiązkowy
![]()
![]() Przeprowadzany na podstawie wymagań egzaminacyjnych, zawierających ograniczony zakres wymagań podstawy programowej (np. ograniczone wymagania dotyczące funkcji i graniastosłupów, całkowita redukcja wymagań dotyczących brył obrotowych i wymagań z IV etapu edukacyjnego dotyczących ostrosłupów). Dokładniejszy spis znajdziesz poniżej.
Przeprowadzany na podstawie wymagań egzaminacyjnych, zawierających ograniczony zakres wymagań podstawy programowej (np. ograniczone wymagania dotyczące funkcji i graniastosłupów, całkowita redukcja wymagań dotyczących brył obrotowych i wymagań z IV etapu edukacyjnego dotyczących ostrosłupów). Dokładniejszy spis znajdziesz poniżej.
![]()
![]() Czas trwania: 170 minut.
Czas trwania: 170 minut.
![]()
![]() Za rozwiązanie zadań można uzyskać maksymalnie 45 punktów (5 pkt mniej niż w latach ubiegłych), w tym:
Za rozwiązanie zadań można uzyskać maksymalnie 45 punktów (5 pkt mniej niż w latach ubiegłych), w tym:
![]() 28 pkt – zadania zamknięte;
28 pkt – zadania zamknięte;
![]() 17 pkt – zadania otwarte.
17 pkt – zadania otwarte.
![]()
![]() Liczba zadań otwartych: 7 (w latach 2015–2020: 9).
Liczba zadań otwartych: 7 (w latach 2015–2020: 9).
Przedmioty na poziomie rozszerzonym (dodatkowe)
![]()
![]() Przeprowadzany na podstawie wymagań egzaminacyjnych, zawierających ograniczony zakres wymagań podstawy programowej. Dokładniejszy spis znajdziesz poniżej.
Przeprowadzany na podstawie wymagań egzaminacyjnych, zawierających ograniczony zakres wymagań podstawy programowej. Dokładniejszy spis znajdziesz poniżej.
![]()
![]() Przystąpienie do jednego egzaminu na poziomie rozszerzonym – obowiązkowe (zmiana w stosunku do roku 2021, gdzie rozszerzone przedmioty były nieobowiązkowe). Można przystąpić do egzaminu z maksymalnie sześciu przedmiotów dodatkowych.
Przystąpienie do jednego egzaminu na poziomie rozszerzonym – obowiązkowe (zmiana w stosunku do roku 2021, gdzie rozszerzone przedmioty były nieobowiązkowe). Można przystąpić do egzaminu z maksymalnie sześciu przedmiotów dodatkowych.
Co zostało usunięte z wymagań na maturę z matematyki 2021 i 2022?
Wymagania egzaminacyjne dotyczące egzaminu maturalnego z matematyki w roku szkolnym 2020/2021 oraz 2021/2022.
Poniżej wykaz szczegółowych wymagań edukacyjnych z matematyki obowiązujących na egzaminie maturalnym w latach 2015-2022.
Na czerwono oznaczono treści, które NIE obowiązują na egzaminie maturalnym w roku szkolnym 2020/2021 oraz 2021/2022.
Poziom podstawowy
1) Liczby rzeczywiste. Uczeń:
1. przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg);
2. oblicza wartości wyrażeń arytmetycznych (wymiernych);
3. posługuje się w obliczeniach pierwiastkami dowolnego stopnia i stosuje prawa działań na pierwiastkach;
4. oblicza potęgi o wykładnikach wymiernych i stosuje prawa działań na potęgach o wykładnikach wymiernych;
5. wykorzystuje podstawowe własności potęg (również w zagadnieniach związanych z innymi dziedzinami wiedzy, np. fizyką, chemią, informatyką);
6. wykorzystuje definicję logarytmu i stosuje w obliczeniach wzory na logarytm iloczynu, logarytm ilorazu i logarytm potęgi o wykładniku naturalnym;
7. oblicza błąd bezwzględny i błąd względny przybliżenia;
8. posługuje się pojęciem przedziału liczbowego, zaznacza przedziały na osi liczbowej;
9. wykonuje obliczenia procentowe, oblicza podatki, zysk z lokat (również złożonych na procent składany i na okres krótszy niż rok).
2) Wyrażenia algebraiczne. Uczeń:
1. używa wzorów skróconego mnożenia na 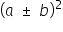 oraz
oraz 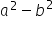
3) Równania i nierówności. Uczeń:
1. sprawdza, czy dana liczba rzeczywista jest rozwiązaniem równania lub nierówności;
2. wykorzystuje interpretację geometryczną układu równań pierwszego stopnia z dwiema niewiadomymi;
3. rozwiązuje nierówności pierwszego stopnia z jedną niewiadomą;
4. rozwiązuje równania kwadratowe z jedną niewiadomą;
5. rozwiązuje nierówności kwadratowe z jedną niewiadomą;
6. korzysta z definicji pierwiastka do rozwiązywania równań typu 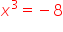 ;
;
7. korzysta z własności iloczynu przy rozwiązywaniu równań typu 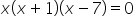 ;
;
8. rozwiązuje proste równania wymierne, prowadzące do równań liniowych lub kwadratowych, np. 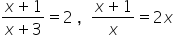 .
.
4) Funkcje. Uczeń:
1. określa funkcje za pomocą wzoru, tabeli, wykresu, opisu słownego;
2. oblicza ze wzoru wartość funkcji dla danego argumentu. Posługuje się poznanymi metodami rozwiązywania równań do obliczenia, dla jakiego argumentu funkcja przyjmuje daną wartość;
3. odczytuje z wykresu własności funkcji (dziedzinę, zbiór wartości, miejsca zerowe, maksymalne przedziały, w których funkcja maleje, rośnie, ma stały znak; punkty, w których funkcja przyjmuje w podanym przedziale wartość największą lub najmniejszą);
4. na podstawie wykresu funkcji 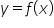 szkicuje wykresy funkcji
szkicuje wykresy funkcji 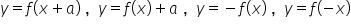 ;
;
5. rysuje wykres funkcji liniowej, korzystając z jej wzoru;
6. wyznacza wzór funkcji liniowej na podstawie informacji o funkcji lub o jej wykresie;
7. interpretuje współczynniki występujące we wzorze funkcji liniowej;
8. szkicuje wykres funkcji kwadratowej, korzystając z jej wzoru;
9. wyznacza wzór funkcji kwadratowej na podstawie pewnych informacji o tej funkcji lub o jej wykresie;
10. interpretuje współczynniki występujące we wzorze funkcji kwadratowej w postaci kanonicznej, w postaci ogólnej i w postaci iloczynowej (o ile istnieje);
11. wyznacza wartość najmniejszą i wartość największą funkcji kwadratowej w przedziale domkniętym;
12. wykorzystuje własności funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych, fizycznych itp. (także osadzonych w kontekście praktycznym);
13. szkicuje wykres funkcji 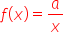 dla danego
dla danego  , korzysta ze wzoru i wykresu tej funkcji do interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi;
, korzysta ze wzoru i wykresu tej funkcji do interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi;
14. szkicuje wykresy funkcji wykładniczych dla różnych podstaw;
15. posługuje się funkcjami wykładniczymi do opisu zjawisk fizycznych, chemicznych, a także w zagadnieniach osadzonych w kontekście praktycznym.
5) Ciągi. Uczeń:
1. wyznacza wyrazy ciągu określonego wzorem ogólnym;
2. bada, czy dany ciąg jest arytmetyczny lub geometryczny;
3. stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu arytmetycznego;
4. stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu geometrycznego.
6) Trygonometria. Uczeń:
1. wykorzystuje definicje i wyznacza wartości funkcji sinus, cosinus i tangens kątów o miarach od 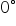 do
do 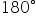 ;
;
2. korzysta z przybliżonych wartości funkcji trygonometrycznych (odczytanych z tablic lub obliczonych za pomocą kalkulatora);
3. oblicza miarę kąta ostrego, dla której funkcja trygonometryczna przyjmuje daną wartość (miarę dokładną albo – korzystając z tablic lub kalkulatora – przybliżoną);
4. stosuje proste zależności między funkcjami trygonometrycznymi: 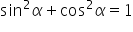 ,
, 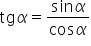 oraz
oraz 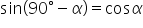 ;
;
5. znając wartość jednej z funkcji: sinus lub cosinus, wyznacza wartości pozostałych funkcji tego samego kąta ostrego.
7) Planimetria. Uczeń:
1. stosuje zależności między kątem środkowym i kątem wpisanym;
2. korzysta z własności stycznej do okręgu i własności okręgów stycznych;
3. rozpoznaje trójkąty podobne i wykorzystuje (także w kontekstach praktycznych) cechy podobieństwa trójkątów;
4. korzysta z własności funkcji trygonometrycznych w łatwych obliczeniach geometrycznych, w tym ze wzoru na pole trójkąta ostrokątnego o danych dwóch bokach i kącie między nimi.
8) Geometria na płaszczyźnie kartezjańskiej. Uczeń:
1. wyznacza równanie prostej przechodzącej przez dwa dane punkty (w postaci kierunkowej lub ogólnej);
2. bada równoległość i prostopadłość prostych na podstawie ich równań kierunkowych;
3. wyznacza równanie prostej, która jest równoległa lub prostopadła do prostej danej w postaci kierunkowej i przechodzi przez dany punkt;
4. oblicza współrzędne punktu przecięcia dwóch prostych;
5. wyznacza współrzędne środka odcinka;
6. oblicza odległość dwóch punktów;
7. znajduje obrazy niektórych figur geometrycznych (punktu, prostej, odcinka, okręgu, trójkąta itp.) w symetrii osiowej względem osi układu współrzędnych i symetrii środkowej względem początku układu.
9) Stereometria. Uczeń:
1. rozpoznaje w graniastosłupach i ostrosłupach kąty między odcinkami (np. krawędziami, krawędziami i przekątnymi, itp.), oblicza miary tych kątów;
2. rozpoznaje w graniastosłupach i ostrosłupach kąt między odcinkami i płaszczyznami (między krawędziami i ścianami, przekątnymi i ścianami), oblicza miary tych kątów;
3. rozpoznaje w walcach i w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami (np. kąt rozwarcia stożka, kąt między tworzącą a podstawą), oblicza miary tych kątów;
4. rozpoznaje w graniastosłupach i ostrosłupach kąty między ścianami;
5. określa, jaką figurą jest dany przekrój prostopadłościanu płaszczyzną;
6. stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości;
10) Elementy statystyki opisowej. Teoria prawdopodobieństwa i kombinatoryka. Uczeń:
1. oblicza średnią ważoną i odchylenie standardowe zestawu danych (także w przypadku danych odpowiednio po grupowanych), interpretuje te parametry dla danych empirycznych;
2. zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania;
3. oblicza prawdopodobieństwa w prostych sytuacjach, stosując klasyczną definicję prawdopodobieństwa.
Poziom rozszerzony
1) Liczby rzeczywiste. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. wykorzystuje pojęcie wartości bezwzględnej i jej interpretację geometryczną, zaznacza na osi liczbowej zbiory opisane za pomocą równań i nierówności typu: 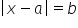 ,
, 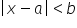 ,
, 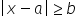 ;
;
2. stosuje w obliczeniach wzór na logarytm potęgi oraz wzór na zamianę podstawy logarytmu.
2) Wyrażenia algebraiczne. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. używa wzorów skróconego mnożenia na 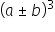 oraz
oraz 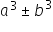 ;
;
2. dzieli wielomiany przez dwumian 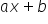 ;
;
3. rozkłada wielomian na czynniki, stosując wzory skróconego mnożenia lub wyłączając wspólny czynnik przed nawias;
4. dodaje, odejmuje i mnoży wielomiany;
5. wyznacza dziedzinę prostego wyrażenia wymiernego z jedną zmienną, w którym w mianowniku występują tylko wyrażenia dające się łatwo sprowadzić do iloczynu wielomianów liniowych i kwadratowych;
6. dodaje, odejmuje, mnoży i dzieli wyrażenia wymierne; rozszerza i (w łatwych przykładach) skraca wyrażenia wymierne.
3) Równania i nierówności. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. stosuje wzory Viete’a;
2. rozwiązuje równania i nierówności liniowe i kwadratowe z parametrem;
3. rozwiązuje układy równań, prowadzące do równań kwadratowych;
4. stosuje twierdzenie o reszcie z dzielenia wielomianu przez dwumian 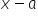 ;
;
5. stosuje twierdzenie o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych;
6. rozwiązuje równania wielomianowe dające się łatwo sprowadzić do równań kwadratowych;
7. rozwiązuje łatwe nierówności wielomianowe;
8. rozwiązuje proste nierówności wymierne typu: 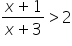 ,
, 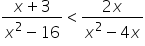 ,
, 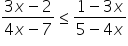 ;
;
9. rozwiązuje równania i nierówności z wartością bezwzględną, o poziomie trudności nie wyższym, niż: 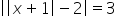 ,
, 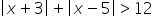 .
.
4) Funkcje. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. na podstawie wykresu funkcji 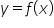 szkicuje wykresy funkcji
szkicuje wykresy funkcji 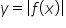 ,
, 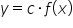 ,
, 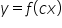 ;
;
2. szkicuje wykresy funkcji logarytmicznych dla różnych podstaw;
3. posługuje się funkcjami logarytmicznym i do opisu zjawisk fizycznych, chemicznych, a tak że w zagadnieniach osadzonych w kontekście praktycznym;
4. szkicuje wykres funkcji określonej w różnych przedziałach różnymi wzorami; odczytuje własności takiej funkcji z wykresu.
5) Ciągi. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. wyznacza wyrazy ciągu określonego wzorem rekurencyjnym;
2. oblicza granice ciągów, korzystając z granic ciągów typu 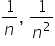 oraz z twierdzeń o działaniach na granicach ciągów;
oraz z twierdzeń o działaniach na granicach ciągów;
3. rozpoznaje szeregi geometryczne zbieżne i oblicza ich sumy.
6) Trygonometria. Uczeń:
1. stosuje miarę łukową, zamienia miarę łukową kąta na stopniową i odwrotnie;
2. wykorzystuje definicje i wyznacza wartości funkcji sinus, cosinus i tangens dowolnego kąta o mierze wyrażonej w stopniach lub radianach (przez sprowadzenie do przypadku kąta ostrego);
3. wykorzystuje okresowość funkcji trygonometrycznych;
4. posługuje się wykresami funkcji trygonometrycznych (np. gdy rozwiązuje nierówności typu 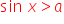 ,
,  ,
, 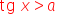 );
);
5. stosuje wzory na sinus i cosinus sumy i różnicy kątów, sumę i różnicę sinusów i cosinusów kątów;
6. rozwiązuje równania i nierówności trygonometryczne typu 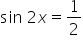 ,
, 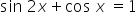 ,
, 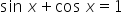 ,
, 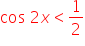 .
.
7) Planimetria. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. stosuje twierdzenia charakteryzujące czworokąty wpisane w okrąg i czworokąty opisane na okręgu;
2. stosuje twierdzenie Talesa i twierdzenie odwrotne do twierdzenia Talesa do obliczania długości odcinków i ustalania równoległości prostych;
3. znajduje obrazy niektórych figur geometrycznych w jednokładności (odcinka, trójkąta, czworokąta itp.);
4. rozpoznaje figury podobne i jednokładne; wykorzystuje (także w kontekstach praktycznych) ich własności;
5. znajduje związki miarowe w figurach płaskich z zastosowaniem twierdzenia sinusów i twierdzenia cosinusów.
8) Geometria na płaszczyźnie kartezjańskiej. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. interpretuje graficznie nierówność liniową z dwiema niewiadomymi oraz układy takich nierówności;
2. bada równoległość i prostopadłość prostych na podstawie ich równań ogólnych;
3. wyznacza równanie prostej, która jest równoległa lub prostopadła do prostej danej w postaci ogólnej i przechodzi przez dany punkt;
4. oblicza odległość punktu od prostej;
5. posługuje się równaniem okręgu 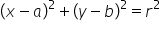 oraz opisuje koła za pomocą nierówności;
oraz opisuje koła za pomocą nierówności;
6. wyznacza punkty wspólne prostej i okręgu;
7. oblicza współrzędne oraz długość wektora; dodaje i odejmuje wektory oraz mnoży je przez liczbę. Interpretuje geometrycznie działania na wektorach;
8. stosuje wektory do opisu przesunięcia wykresu funkcji.
9) Stereometria. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. określa, jaką figurą jest dany przekrój sfery płaszczyzną;
2. określa, jaką figurą jest dany przekrój graniastosłupa lub ostrosłupa płaszczyzną.
10) Elementy statystyki opisowej. Teoria prawdopodobieństwa i kombinatoryka. Uczeń spełnia wymagania określone dla zakresu podstawowego, a ponadto:
1. wykorzystuje wzory na liczbę permutacji, kombinacji, wariacji i wariacji z powtórzeniami do zliczania obiektów w bardziej złożonych sytuacjach kombinatorycznych;
2. oblicza prawdopodobieństwo warunkowe;
3. korzysta z twierdzenia o prawdopodobieństwie całkowitym.
11) Rachunek różniczkowy. Uczeń:
1. oblicza granice funkcji (i granice jednostronne), korzystając z twierdzeń o działaniach na granicach i z własności funkcji ciągłych;
2. oblicza pochodne funkcji wymiernych;
3. korzysta z geometrycznej i fizycznej interpretacji pochodnej;
4. korzysta z własności pochodnej do wyznaczenia przedziałów monotoniczności funkcji;
5. znajduje ekstrema funkcji wielomianowych i wymiernych;
6. stosuje pochodne do rozwiązywania zagadnień optymalizacyjnych.
Źródła:
https://www.gov.pl/web/edukacja-i-nauka/wymagania-na-egzaminach-osmoklasisty-i-maturalnym