Matura 2023 ARKUSZ POKAZOWY marzec 2022 (poziom podstawowy). CKE matematyka – nowa formuła
Anna Zalewska
Absolwentka matematyki na Politechnice Śląskiej.
Korepetytor z 12-letnim doświadczeniem. Trener i wykładowca na Uniwersytecie Śląskim Maturzystów przy Uniwersytecie Śląskim w Katowicach. Certyfikowany nauczyciel MathRiders.
Mieszka w Chorzowie. Jest ratownikiem wodnym i członkiem Zarządu Oddziału Miejskiego WOPR. Lubi piec ciasta, ciasteczka, torty i przygotowywać różne słodkości.
W tym roku szkolnym absolwenci liceum podejdą po raz pierwszy do matury w nowej formule 2023 (uczniowie kończący technikum podchodzą po raz ostatni jeszcze do “starej” formuły).
Centralna Komisja Egzaminacyjna przygotowała w marcu 2022 roku przykładowe arkusze maturalne, zarówno na poziomie podstawowym, jak i rozszerzonym.
Poniżej znajdziesz omówione zadania krok po kroku z arkusza PODSTAWOWEGO. Zapraszam również do obejrzenia rozwiązań w formie graficznej, zamieszczonej na końcu wpisu. 
Co się zmieniło w porównaniu z poprzednimi maturami? Oprócz zmian w postawie programowej pojawiły się nowe typy zadań. Nie ma tylko zadań zamkniętych a, b, c, d i zadań otwartych. Pojawiły się zadania “zamknięte” typu prawda/fałsz, zadania z wyborem dwóch odpowiedzi (a nie tylko jednej), zadania z wyborem odpowiedzi i jej uzasadnienia, oraz tzw. wiązka zadań, czyli kilka poleceń do jednego zadania, zarówno otwartych jak i zamkniętych.
Zapraszam oczywiście do rozwiązań wcześniejszych matur, z CKE (majowych, dodatkowych z czerwca oraz poprawkowych), a także matur próbnych z Operonu i Nowej Ery. Są świetną formą nauki także dla osób zdających nową formułę. Znajdziecie je wszystkie na naszym kanale na YouTube.
SPIS TREŚCI:
0:00 – Wstęp
7:09 – Zadanie 1 zamknięte – 1p (potęgi: działania na potęgach)
9:38 – Zadanie 2 zamknięte – 1p (logarytmy: odejmowanie dwóch logarytmów)
13:17 – Zadanie 3 zamknięte – 1p (kombinatoryka: ile jest liczb trzycyfrowych bez cyfry 2)
15:03 – Zadanie 4 zamknięte – 1p (wzory skróconego mnożenia)
18:46 – Zadanie 5 zamknięte – 2p (kąty przyległe i wierzchołkowe, układ równań)
26:12 – Zadanie 6 zamknięte – 1p (wielomiany: pierwiastek wielomianu)
27:49 – Zadanie 7 zamknięte – 1p (równanie wymierne, pierwiastki, dziedzina ułamka)
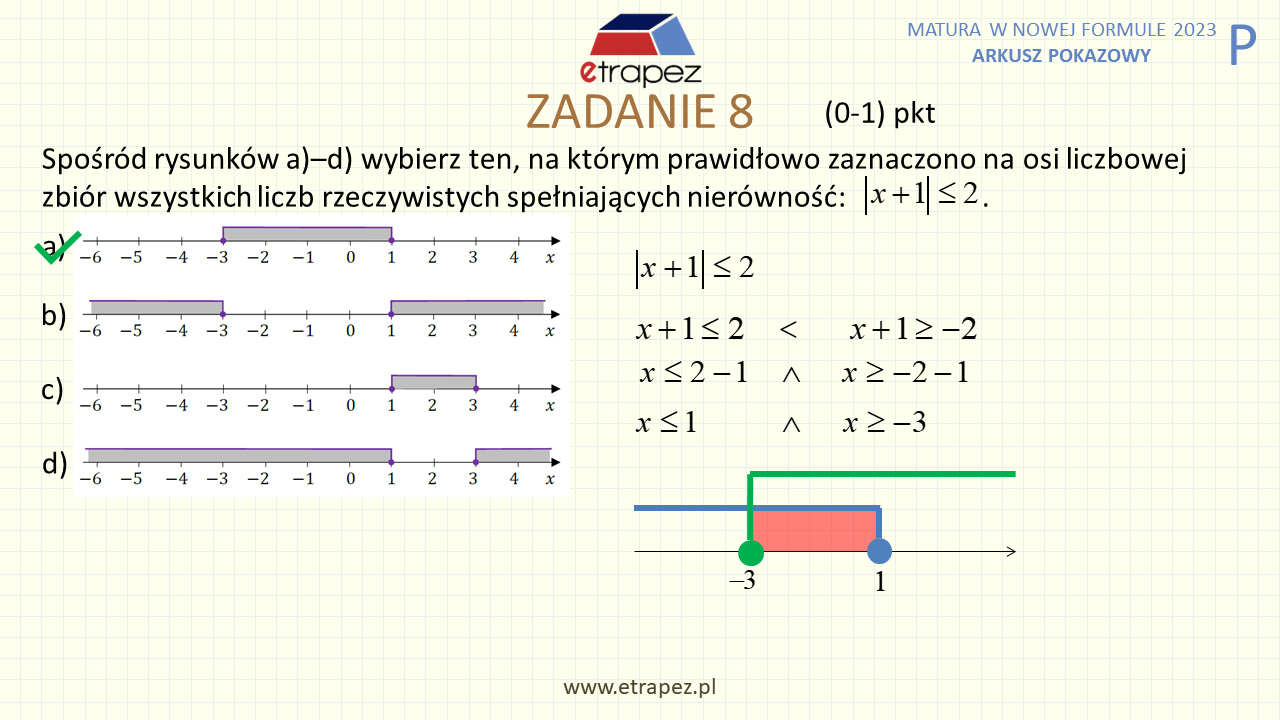
33:31 – Zadanie 8 zamknięte – 1p (nierówność z wartością bezwzględną, oś liczbowa)
38:52 – Zadanie 9 otwarte – 2p (dowód algebraiczny: wykaż, że wyrażenie jest podzielne przez 8)
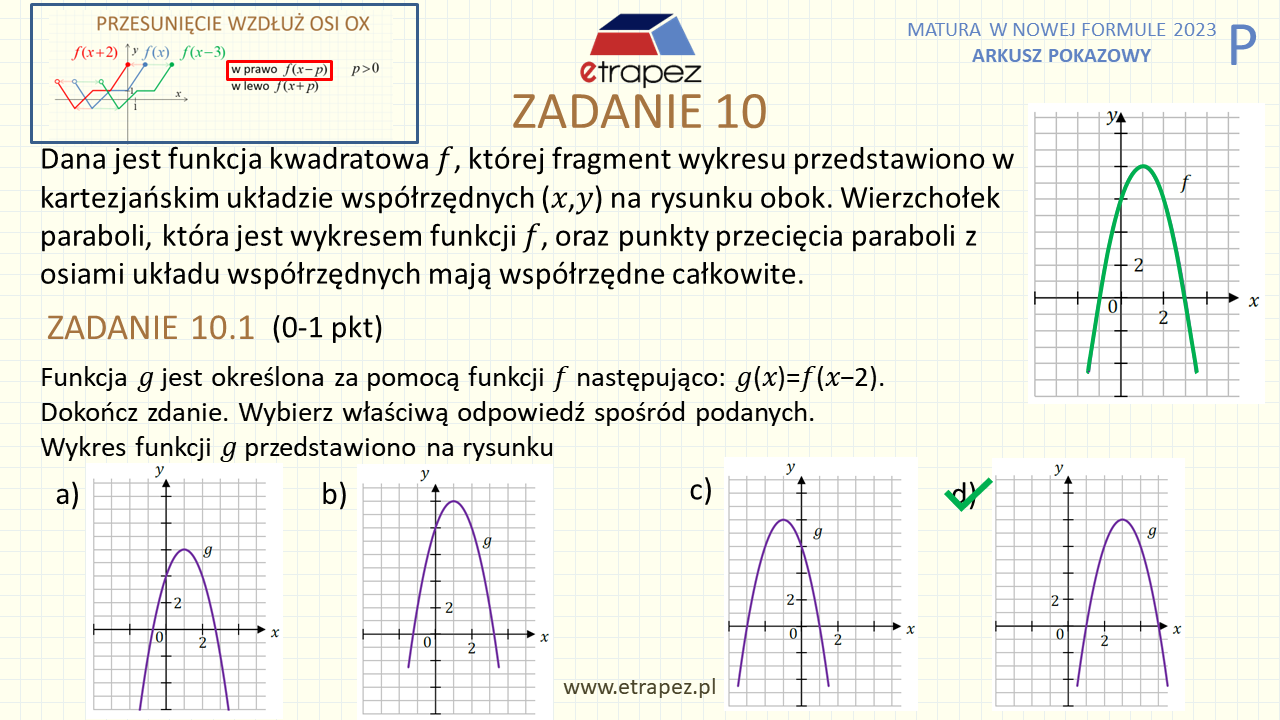
45:45 – Zadanie 10 wiązka zadań – 1+1+3p (funkcja kwadratowa: przesunięcie wykresu, nierówność kwadratowa, wzór w postaci kanonicznej)
55:26 – Zadanie 11 zamknięte – 1p (funkcja liniowa: znaki współczynników)
57:36 – Zadanie 12 zamknięte – 1p (funkcja: wzór funkcji z opisu słownego)
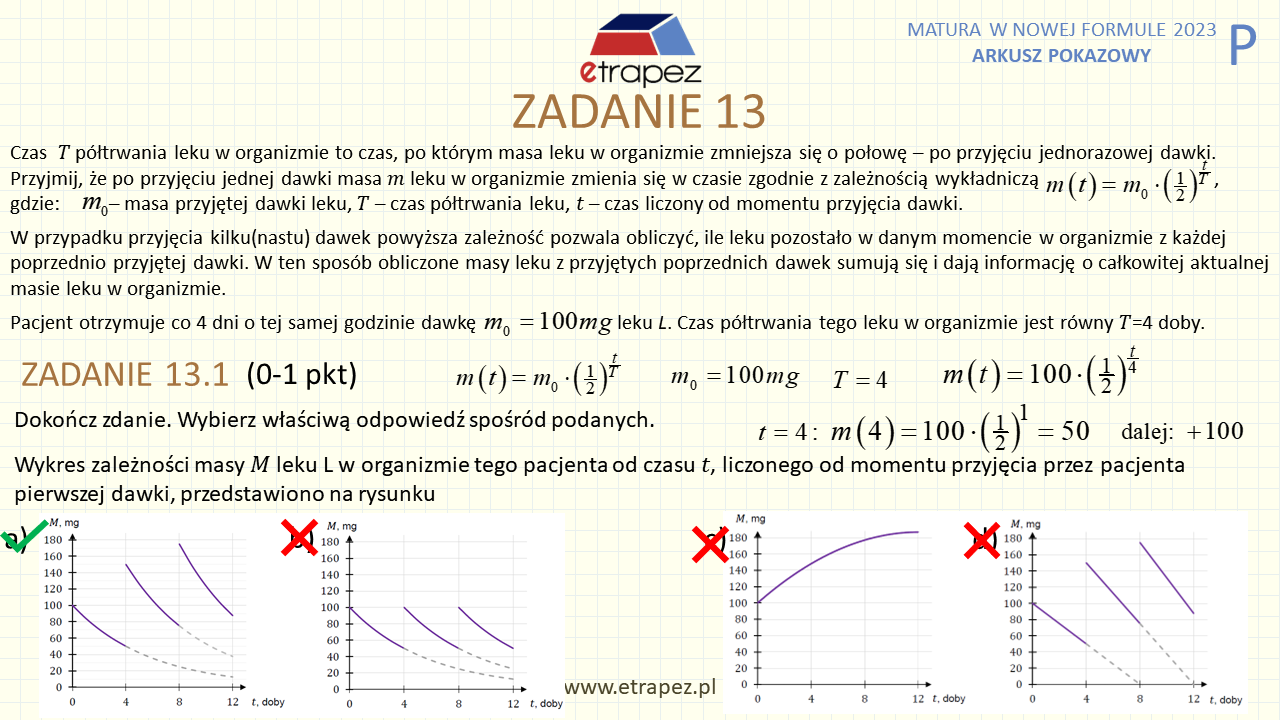
1:02:31 – Zadanie 13 wiązka zadań – 1+3p (funkcja wykładnicza: zadanie z treścią, wykres, suma ciągu geometrycznego)
1:18:25 – Zadanie 14 zamknięte – 1p (lokata w banku, procent składany)
1:21:04 – Zadanie 15 prawda/fałsz – 1p (ciąg arytmetyczny, trzy pierwsze wyrazy)
1:24:57 – Zadanie 16 prawda/fałsz – 1p (twierdzenie cosinusów)
1:31:22 – Zadanie 17 zamknięte – 1p (równanie okręgu)
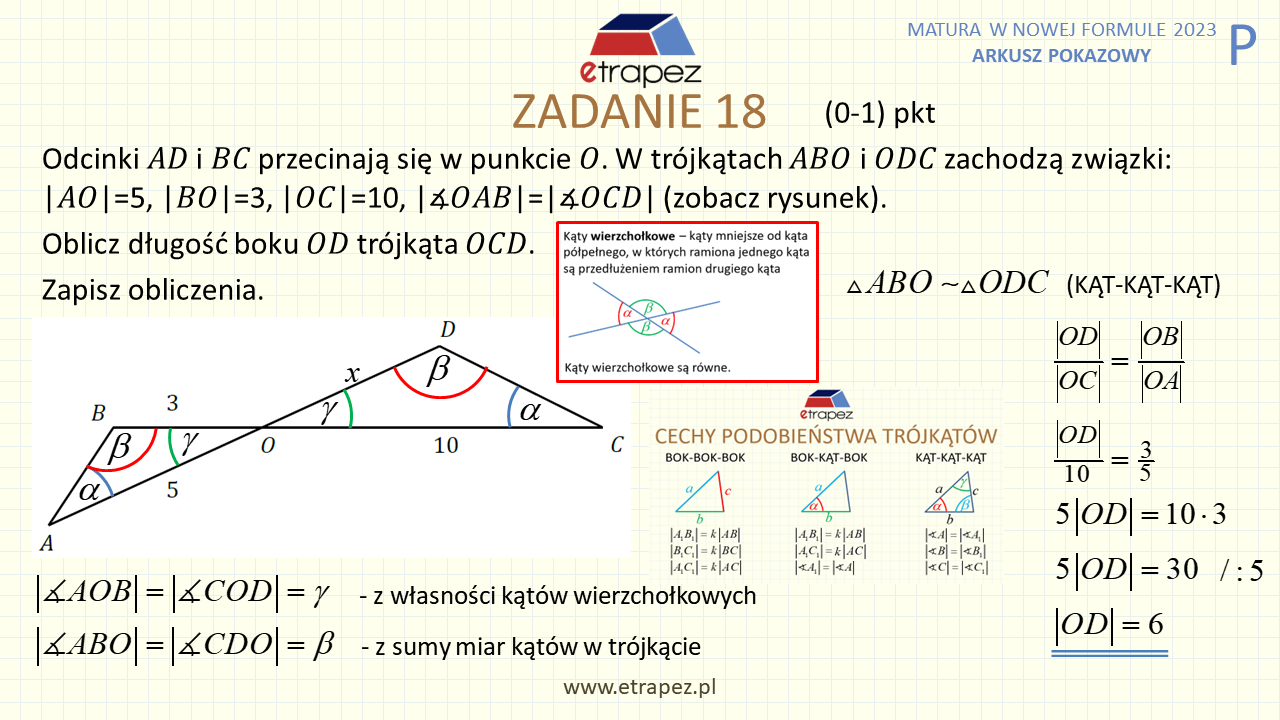
1:33:04 – Zadanie 18 otwarte – 1p (trójkąty podobne, długość boku)
1:36:59 – Zadanie 19 zamknięte – 2p (proste równoległe, proste prostopadłe)
1:40:00 – Zadanie 20 zamknięte – 1p (długość odcinka: kwadrat, dwa przeciwległe wierzchołki, długość przekątnej)
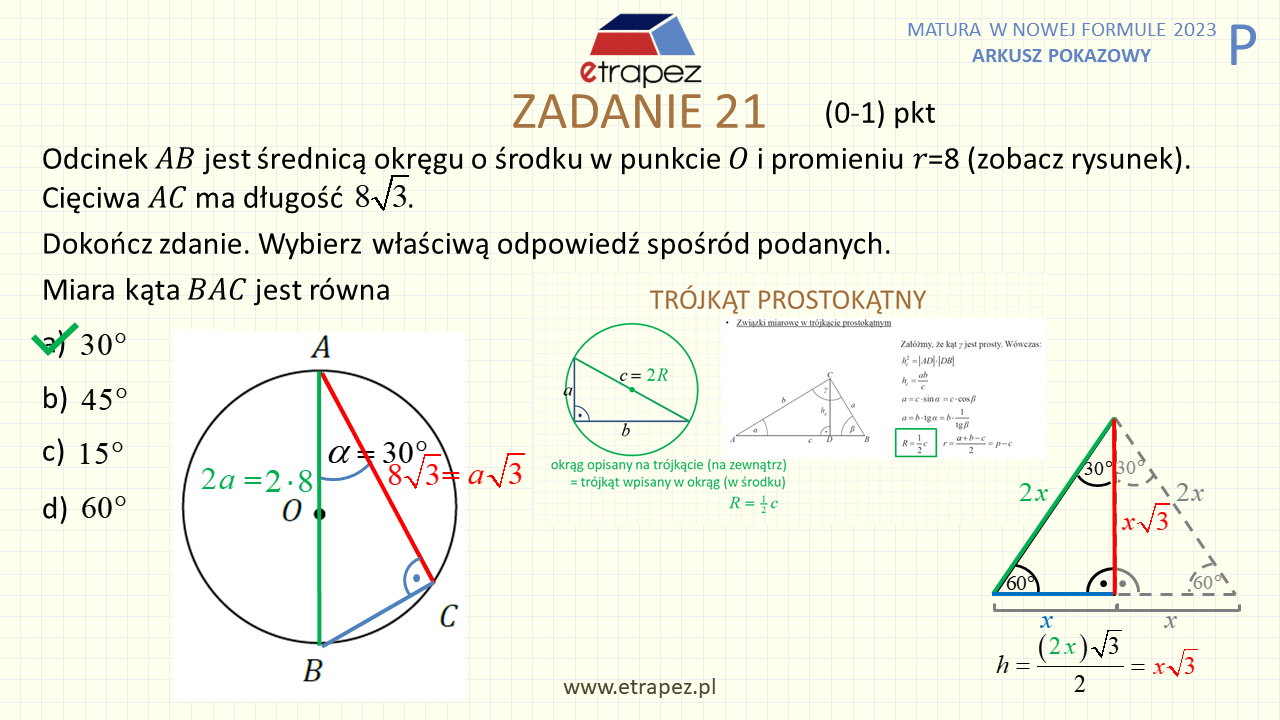
1:43:16 – Zadanie 21 zamknięte – 1p (kąty w okręgu: kąt między średnicą a cięciwą, kąty w trójkącie prostokątnym)
1:47:35 – Zadanie 22 zamknięte – 1p (trygonometria: tangens kąta, podane wyrażenie, jedynka trygonometryczna)
1:49:33 – Zadanie 23 z uzasadnieniem – 1p (trójkąty podobne, skala podobieństwa)
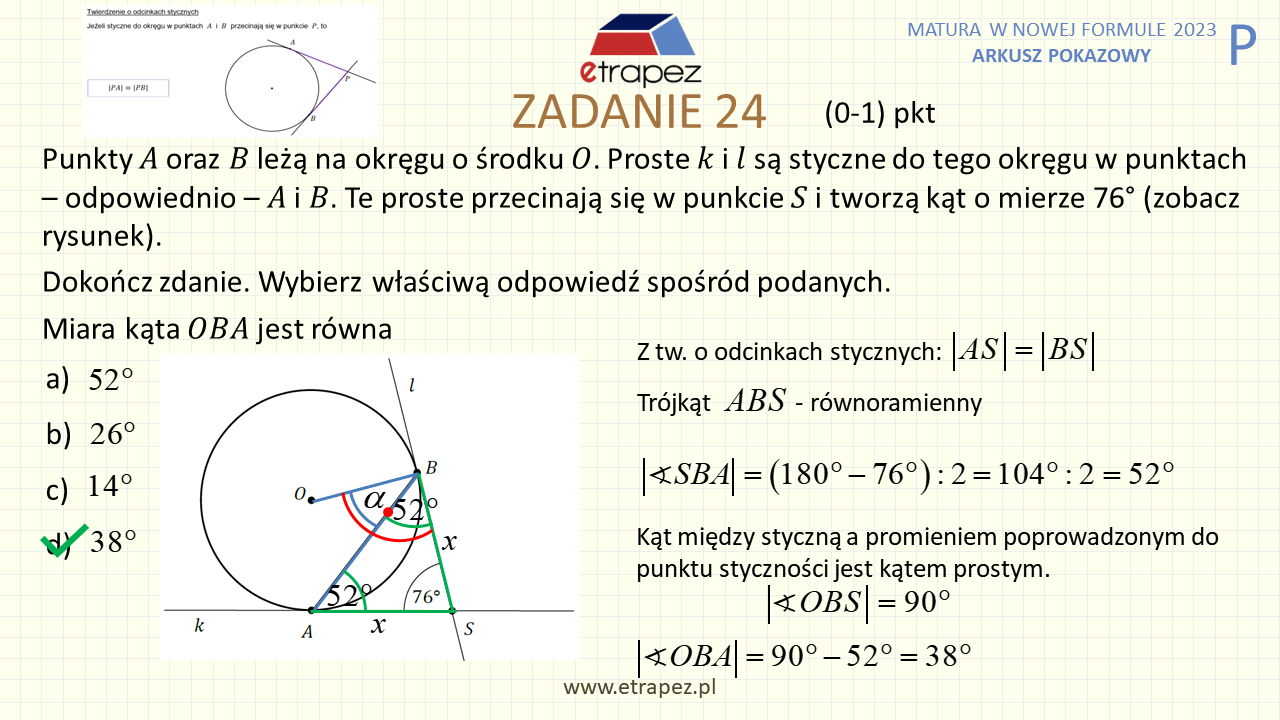
1:52:56 – Zadanie 24 zamknięte – 1p (katy w okręgu: twierdzenie o odcinkach stycznych, styczna)
1:55:38 – Zadanie 25 zamknięte – 1p (graniastosłup: podana powierzchnia boczna, długość krawędzi podstawy)
1:58:24 – Zadanie 26 zamknięte – 1p (ostrosłupy podobne, skala podobieństwa, objętość)
2:01:48 – Zadanie 27 zamknięte – 1p (graniastosłup: kąt między przekątną ściany bocznej a ścianą boczną)
2:07:34 – Zadanie 28 otwarte – 3p (prawdopodobieństwo: losowanie liczby czterocyfrowej, suma cyfr równa trzy)
2:12:55 – Zadanie 29 otwarte – 4p (optymalizacja: funkcja kwadratowa, równoległobok, bok x, podany obwód i kąt ostry, dziedzina i pole)
2:21:59 – Zadanie 30 wiązka zadań – 1+1p (mediana, dominanta)
2:27:57 – Uwagi końcowe
Kurs MATURA PODSTAWOWA stanowi kompleksowe przygotowanie do matury podstawowej zarówno w “starej” formule 2015, jak i “nowej” formule 2023.
Sprawdź:
►Formuła 2023 oraz 2015: Kurs Matura Podstawowa
Ten Kurs Maturalny to taka solidna powtórka przed maturą. Każda lekcja to nagranie z 40 zadaniami z danego działu. Zadania te są ułożone zgodnie ze schematami pojawiającymi się w arkuszach, więc sumienne przerobienie kursu na pewno pomoże lepiej poczuć się w temacie i oswoi z typowymi zadaniami.
Do każdej lekcji dołączony jest plik z zadaniami domowymi, więc z każdego działu mamy 40 zadań na nagraniu + 40 analogicznych do samodzielnego przerobienia.
Na nagraniu wszystko tłumaczone jest od podstaw, tak żeby zrozumieć, zobaczyć różne przykłady. Do tego często mówię o tym, jak sobie pomóc, jeśli jednak zadanko nie podeszło i trzeba trochę pokombinować, użyć jakichś trików i własności, żeby nawet bez obliczeń zaznaczyć w zadaniu zamkniętym prawidłową odpowiedź.
Wszystkie nagrania z poziomu podstawowego w formule 2015 mają łącznie blisko 42h, w formule 2023 mają ponad 44h. Kurs jest więc pełen wiedzy, która na maturze się przyda albo wręcz jest niezbędna. Na pewno dużo pomoże w przygotowaniach do matury. 
Zachęcamy do zajrzenia na nasz kanał i do playlisty z omówionymi Arkuszami maturalnymi (CKE, Operon, Nowa Era).
Kurs MATURA ROZSZERZONA stanowi kompleksowe przygotowanie do matury rozszerzonej zarówno w “starej” formule 2015, jak i “nowej” formule 2023.
Sprawdź:
►Formuła 2023 oraz 2015: Kurs Matura Rozszerzona
Kursem, który tłumaczy wszystko „co i jak”, czyli tak podręcznikowo, od deski do deski, jest KURS FUNKCJE Szkoła Średnia oraz KURS PLANIMETRIA. Planujemy w przyszłości takie podręcznikowe Kursy zrobić z wszystkich działów.
Kurs Funkcje omawia dokładnie wszystkie zagadnienia podstawowe funkcji (m.in. dziedzina, zbiór wartości, miejsca zerowe itp.), przesunięcia funkcji, funkcja liniowa, funkcja kwadratowa, wykładnicza, logarytmiczna oraz wymierna.
► Kurs Funkcje Szkoła Średnia (poziom podstawowy i rozszerzony, wszystkie tematy kompleksowo omówione).
Zapraszamy także do drugiego tematycznego Kursu Planimetria – omawiającego WSZYSTKIE zagadnienia na poziomie podstawowym jak i rozszerzonym. Przedstawione są tutaj szczegółowo: pojęcia wstępne, wektory, trójkąty, czworokąty, wielokąty, koła i okręgi oraz zadania z dowodami w planimetrii.
► Kurs Planimetria: Wprowadzenie, Trójkąty i Czworokąty
► Kurs Planimetria: Wielokąty, Okręgi i Dowody
Zapraszam również do obejrzenia rozwiązań w formie graficznej:
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
