W całkach nieoznaczonych wymiernych, jak wiemy, często należy rozłożyć mianownik funkcji podcałkowej na czynniki i rozłożyć dalej na ułamki proste.
Samo rozłożenie na czynniki jednak może być często kłopotliwe.
Typowe sytuacje
Z prostymi sytuacjami typu:
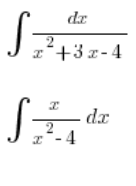
Damy sobie radę:
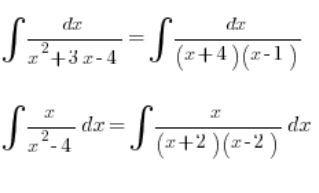
Jeśli w mianowniku będzie wielomian trzeciego stopnia odpowiednio „ustawiony” również damy jeszcze radę:
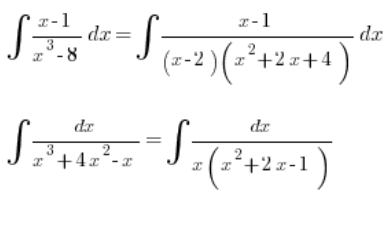
Mianownik z nieprzyjaznym wielomianem trzeciego stopnia
Problem zaczyna się wtedy, kiedy w mianowniku jest wielomian trzeciego stopnia bardziej „nieprzyjazny” do rozkładu, na przykład:
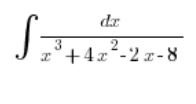
Głęboki wdech.
Opanowujemy panikę.
Takie rzeczy (rozłożenie tego typu wielomianu na czynniki) robiło się już w szkole średniej i to na poziomie podstawowym.
Wystarczy sprytna sztuczka:
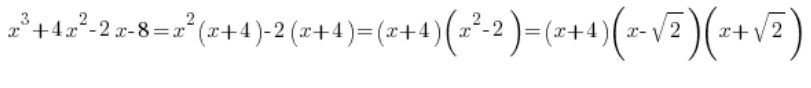
Pamiętamy? Na pewno tak…
Możemy więc rozłożyć wielomian w mianowniku:
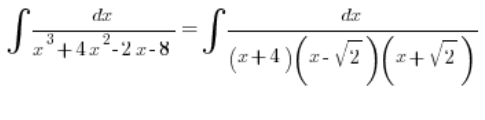
I dalej dziarsko rozkładać na trzy ułamki proste, jak nam reguły każą.
Jeszcze trudniejszy rozkład na czynniki
A co z taką sytuacją? Pamiętamy ze średniej (to już raczej zakres rozszerzony)?
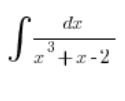
Tu było trochę gorzej. Środkowy składnik trzeba było rozbić na dwa:
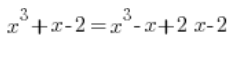
I dalej już po staremu:
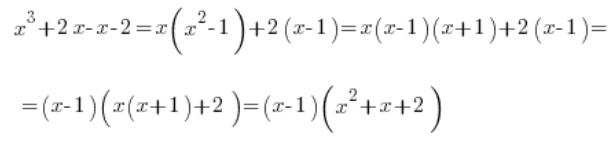
Czyli całkę należy zapisać:
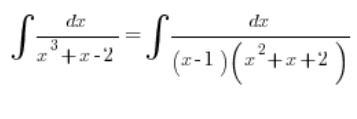
I liczyć spokojnie dalej.
Metody rozkładu mianownika na czynniki w całkach wymiernych
Ogólnie pamiętaj w całkach wymiernych, że jeśli przyjdzie do rozkładu na czynniki wielomianu wszystkie chwyty ze szkoły średniej są dozwolone, a mogą to być jeszcze na przykład:
- rozkład niektórych wielomianów 4-go stopnia przez podstawienie pomocnicze

- szukanie „na ślepo” pierwiastka i dzielenie wielomianu, żeby obniżyć jego stopnień
Oczywiście gadamy już teraz tylko o trudniejszych całkach nieoznaczonych wymiernych, których w wielu (większości?) uczelni nawet się nie wprowadza!


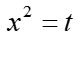

3 Komentarzy
Izabela
A gdy mam całkę 1/(x^3-4x^2+5-2) ? To jak rozłożyć ten mianownik?
Joanna Grochowska
Chodzi o rozłożenie mianownika: \displaystyle {{x}^{3}}-4{{x}^{{^{2}}}}+5x-2?
Jest to równanie 3-go stopnia, nie widzę tu zastosowania żadnego wzoru skróconego mnożenia wprost, więc chcę sprowadzić to równanie do stopnia 2-go (a potem zastosować deltę).
Wykorzystam do tego tzw SCHEMAT HORNERA
Na początku muszę znaleźć jeden z pierwiastków tego wielomianu.
Najpierw wypisuje możliwe liczby jakie mogą być pierwiastkami (są to dzielniki wyrazu wolnego: \displaystyle \pm 1,\pm 2)
Następnie sprawdzam dla którego z dzielników wartość wielomianu równa się zero
(bo x jest pierwiastkiem, gdy f(x)=0 )
\displaystyle \begin{matrix}w(-1)={{(-1)}^{3}}-4\cdot {{(-1)}^{{^{2}}}}+5\cdot (-1)-2=-1-4-5-2=-12\ne 0 \\ w(1)={{1}^{3}}-4\cdot {{1}^{{^{2}}}}+5\cdot 1-2=1-4+5-2=0\end{matrix}
Mam więc już pierwsze rozwiązanie równania: x=1.
Sprowadzam dany wielomian do stopnia o 1 niższy za pomocą schematu Hornera (opisany np tutaj: http://matematyka.pisz.pl/strona/1401.html )
Po podzieleniu powinniśmy otrzymać wielomian:
\displaystyle (x-1)({{x}^{2}}-3x+2)
Wyliczam pierwiastki z równania kwadratowego:
\displaystyle \begin{matrix}\Delta ={{b}^{2}}-4ac={{(-3)}^{2}}-4\cdot 1\cdot 2=9-8=1\sqrt{\Delta }=1 \\ {{x}_{1}}=\frac{{-b-\sqrt{\Delta }}}{{2a}}=\frac{{-(-3)-1}}{2}=1 \\ {{x}_{1}}=\frac{{-b+\sqrt{\Delta }}}{{2a}}=\frac{{-(-3)+1}}{2}=2\end{matrix}
Mam więc rozłożony mianownik: \displaystyle {{x}^{3}}-4{{x}^{{^{2}}}}+5x-2=(x-1)(x-1)(x-2)={{(x-1)}^{2}}(x-2)
Kajetan
Panie Krystianie! Uratował Pan tyłek wielu studentom.